
Question Number 161256 by cortano last updated on 15/Dec/21
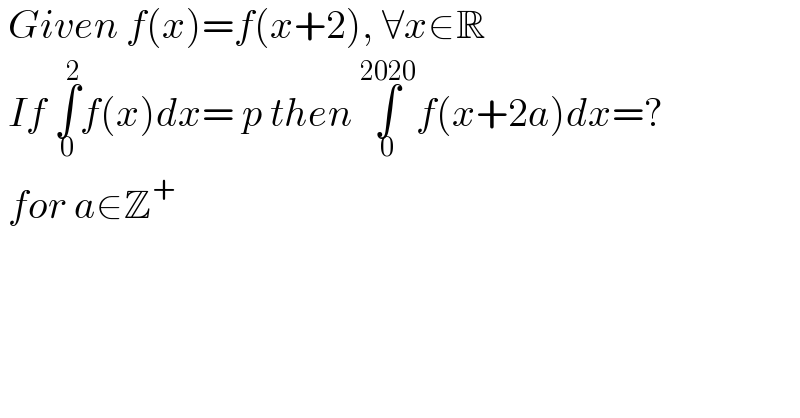
$$\:{Given}\:{f}\left({x}\right)={f}\left({x}+\mathrm{2}\right),\:\forall{x}\in\mathbb{R} \\ $$$$\:{If}\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}=\:{p}\:{then}\:\underset{\mathrm{0}} {\overset{\mathrm{2020}} {\int}}{f}\left({x}+\mathrm{2}{a}\right){dx}=? \\ $$$$\:{for}\:{a}\in\mathbb{Z}^{+} \\ $$
Answered by talminator2856791 last updated on 17/Dec/21
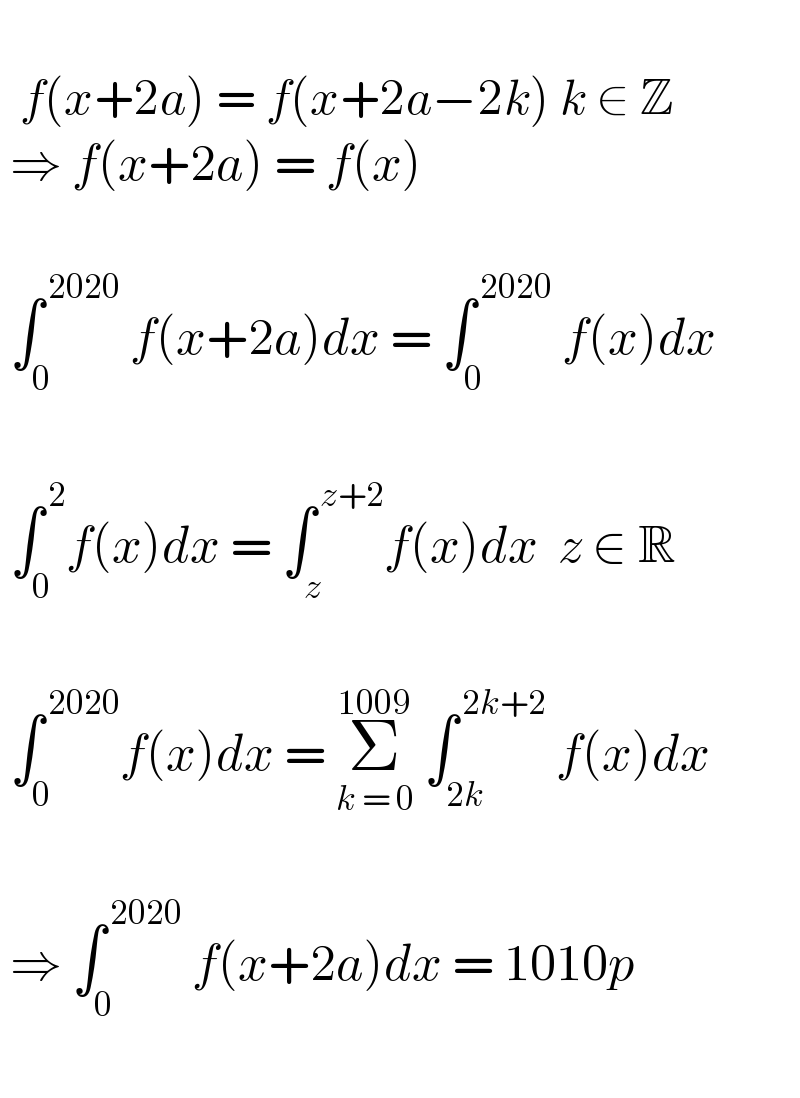
$$\: \\ $$$$\:\:{f}\left({x}+\mathrm{2}{a}\right)\:=\:{f}\left({x}+\mathrm{2}{a}−\mathrm{2}{k}\right)\:{k}\:\in\:\mathbb{Z} \\ $$$$\:\Rightarrow\:{f}\left({x}+\mathrm{2}{a}\right)\:=\:{f}\left({x}\right) \\ $$$$\: \\ $$$$\:\int_{\mathrm{0}} ^{\:\mathrm{2020}} \:{f}\left({x}+\mathrm{2}{a}\right){dx}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{2020}} \:{f}\left({x}\right){dx}\: \\ $$$$\: \\ $$$$\:\int_{\mathrm{0}} ^{\:\mathrm{2}} {f}\left({x}\right){dx}\:=\:\int_{{z}} ^{\:{z}+\mathrm{2}} {f}\left({x}\right){dx}\:\:{z}\:\in\:\mathbb{R} \\ $$$$\: \\ $$$$\:\int_{\mathrm{0}} ^{\:\mathrm{2020}} {f}\left({x}\right){dx}\:=\:\underset{{k}\:=\:\mathrm{0}} {\overset{\mathrm{1009}} {\sum}}\:\int_{\mathrm{2}{k}} ^{\:\mathrm{2}{k}+\mathrm{2}} \:{f}\left({x}\right){dx}\: \\ $$$$\: \\ $$$$\:\Rightarrow\:\int_{\mathrm{0}} ^{\:\mathrm{2020}} \:{f}\left({x}+\mathrm{2}{a}\right){dx}\:=\:\mathrm{1010}{p} \\ $$$$\: \\ $$
