
Question Number 87171 by naka3546 last updated on 03/Apr/20
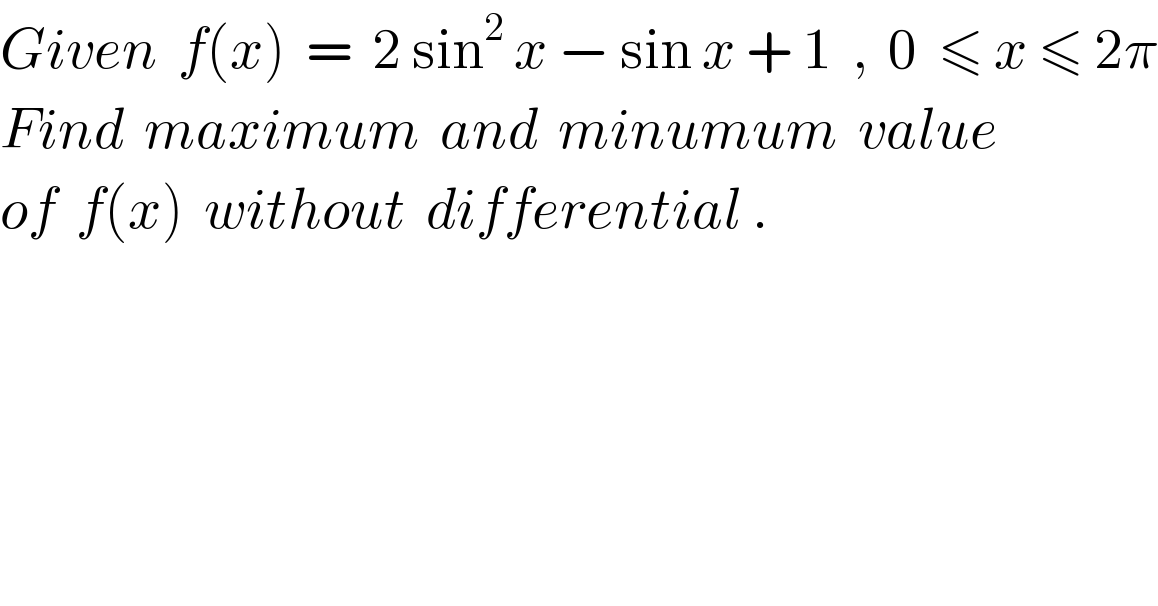
$${Given}\:\:{f}\left({x}\right)\:\:=\:\:\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:{x}\:−\:\mathrm{sin}\:{x}\:+\:\mathrm{1}\:\:,\:\:\mathrm{0}\:\:\leqslant\:{x}\:\leqslant\:\mathrm{2}\pi \\ $$$${Find}\:\:{maximum}\:\:{and}\:\:{minumum}\:\:{value} \\ $$$${of}\:\:{f}\left({x}\right)\:\:{without}\:\:{differential}\:. \\ $$
Commented by john santu last updated on 03/Apr/20
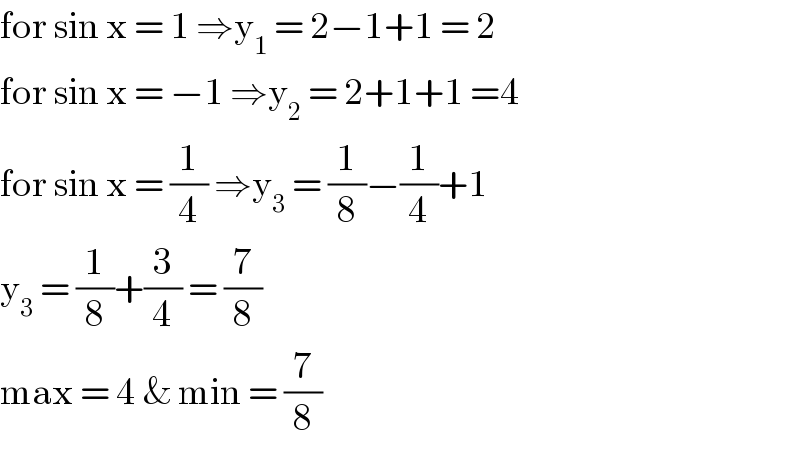
$$\mathrm{for}\:\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{1}\:\Rightarrow\mathrm{y}_{\mathrm{1}} \:=\:\mathrm{2}−\mathrm{1}+\mathrm{1}\:=\:\mathrm{2} \\ $$$$\mathrm{for}\:\mathrm{sin}\:\mathrm{x}\:=\:−\mathrm{1}\:\Rightarrow\mathrm{y}_{\mathrm{2}} \:=\:\mathrm{2}+\mathrm{1}+\mathrm{1}\:=\mathrm{4} \\ $$$$\mathrm{for}\:\mathrm{sin}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{y}_{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1} \\ $$$$\mathrm{y}_{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{3}}{\mathrm{4}}\:=\:\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$\mathrm{max}\:=\:\mathrm{4}\:\&\:\mathrm{min}\:=\:\frac{\mathrm{7}}{\mathrm{8}} \\ $$
Commented by mr W last updated on 03/Apr/20
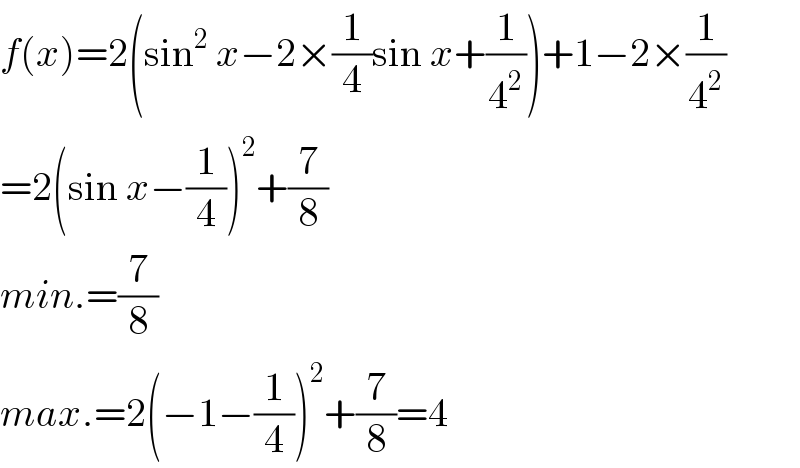
$${f}\left({x}\right)=\mathrm{2}\left(\mathrm{sin}^{\mathrm{2}} \:{x}−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:{x}+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }\right)+\mathrm{1}−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\left(\mathrm{sin}\:{x}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{8}} \\ $$$${min}.=\frac{\mathrm{7}}{\mathrm{8}} \\ $$$${max}.=\mathrm{2}\left(−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{8}}=\mathrm{4} \\ $$
