
Question Number 129009 by bramlexs22 last updated on 12/Jan/21
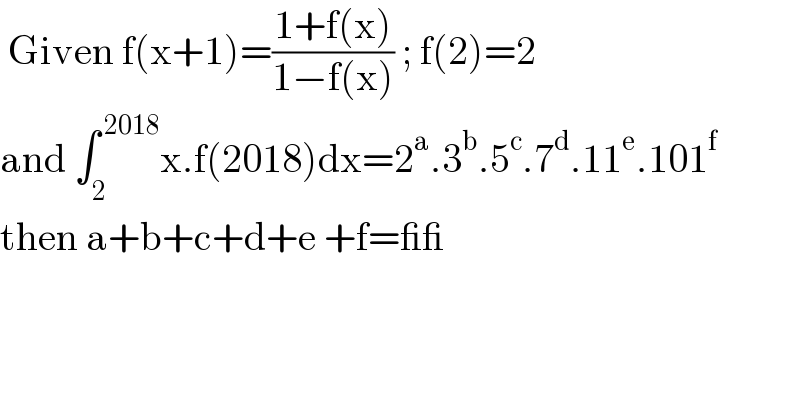
$$\:\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)=\frac{\mathrm{1}+\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{f}\left(\mathrm{x}\right)}\:;\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{2} \\ $$$$\mathrm{and}\:\int_{\mathrm{2}} ^{\:\mathrm{2018}} \mathrm{x}.\mathrm{f}\left(\mathrm{2018}\right)\mathrm{dx}=\mathrm{2}^{\mathrm{a}} .\mathrm{3}^{\mathrm{b}} .\mathrm{5}^{\mathrm{c}} .\mathrm{7}^{\mathrm{d}} .\mathrm{11}^{\mathrm{e}} .\mathrm{101}^{\mathrm{f}} \\ $$$$\mathrm{then}\:\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}+\mathrm{e}\:+\mathrm{f}=\_\_ \\ $$
Answered by liberty last updated on 12/Jan/21
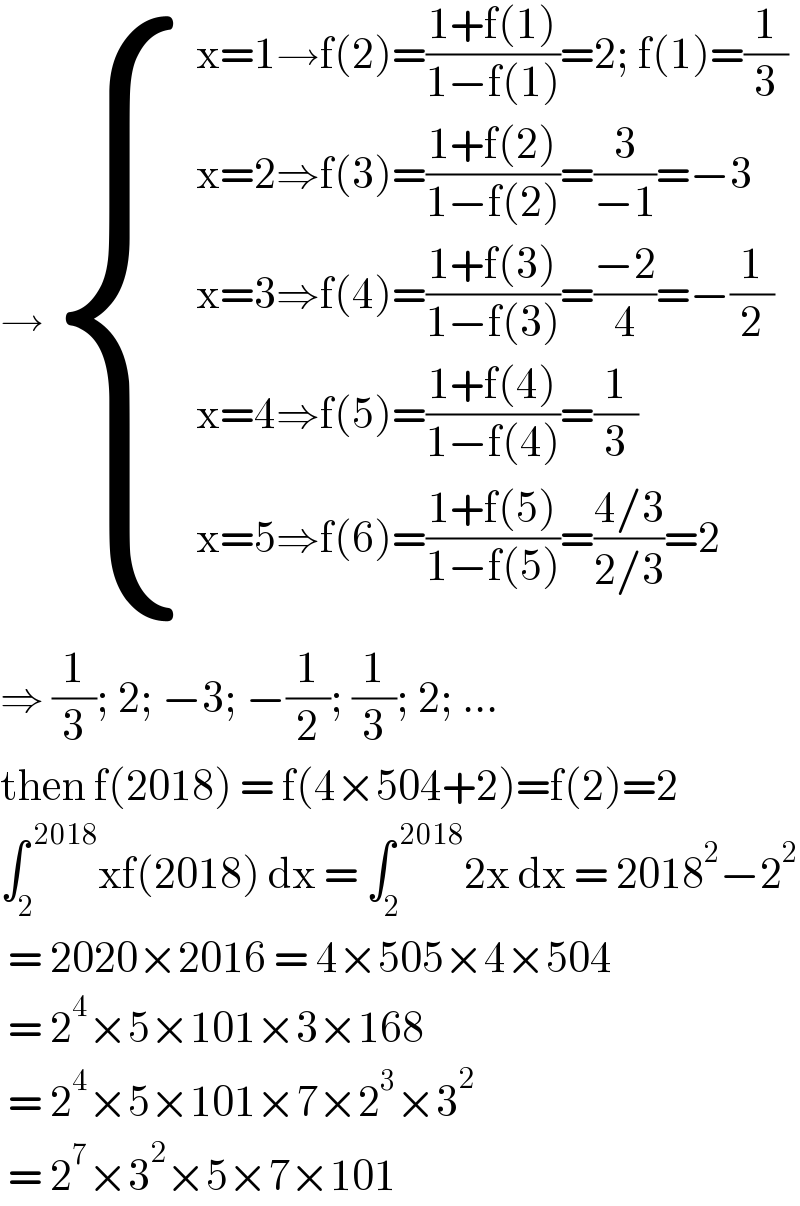
$$\rightarrow\begin{cases}{\mathrm{x}=\mathrm{1}\rightarrow\mathrm{f}\left(\mathrm{2}\right)=\frac{\mathrm{1}+\mathrm{f}\left(\mathrm{1}\right)}{\mathrm{1}−\mathrm{f}\left(\mathrm{1}\right)}=\mathrm{2};\:\mathrm{f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{3}}}\\{\mathrm{x}=\mathrm{2}\Rightarrow\mathrm{f}\left(\mathrm{3}\right)=\frac{\mathrm{1}+\mathrm{f}\left(\mathrm{2}\right)}{\mathrm{1}−\mathrm{f}\left(\mathrm{2}\right)}=\frac{\mathrm{3}}{−\mathrm{1}}=−\mathrm{3}}\\{\mathrm{x}=\mathrm{3}\Rightarrow\mathrm{f}\left(\mathrm{4}\right)=\frac{\mathrm{1}+\mathrm{f}\left(\mathrm{3}\right)}{\mathrm{1}−\mathrm{f}\left(\mathrm{3}\right)}=\frac{−\mathrm{2}}{\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{2}}}\\{\mathrm{x}=\mathrm{4}\Rightarrow\mathrm{f}\left(\mathrm{5}\right)=\frac{\mathrm{1}+\mathrm{f}\left(\mathrm{4}\right)}{\mathrm{1}−\mathrm{f}\left(\mathrm{4}\right)}=\frac{\mathrm{1}}{\mathrm{3}}}\\{\mathrm{x}=\mathrm{5}\Rightarrow\mathrm{f}\left(\mathrm{6}\right)=\frac{\mathrm{1}+\mathrm{f}\left(\mathrm{5}\right)}{\mathrm{1}−\mathrm{f}\left(\mathrm{5}\right)}=\frac{\mathrm{4}/\mathrm{3}}{\mathrm{2}/\mathrm{3}}=\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{3}};\:\mathrm{2};\:−\mathrm{3};\:−\frac{\mathrm{1}}{\mathrm{2}};\:\frac{\mathrm{1}}{\mathrm{3}};\:\mathrm{2};\:... \\ $$$$\mathrm{then}\:\mathrm{f}\left(\mathrm{2018}\right)\:=\:\mathrm{f}\left(\mathrm{4}×\mathrm{504}+\mathrm{2}\right)=\mathrm{f}\left(\mathrm{2}\right)=\mathrm{2} \\ $$$$\int_{\mathrm{2}} ^{\:\mathrm{2018}} \mathrm{xf}\left(\mathrm{2018}\right)\:\mathrm{dx}\:=\:\int_{\mathrm{2}} ^{\:\mathrm{2018}} \mathrm{2x}\:\mathrm{dx}\:=\:\mathrm{2018}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} \\ $$$$\:=\:\mathrm{2020}×\mathrm{2016}\:=\:\mathrm{4}×\mathrm{505}×\mathrm{4}×\mathrm{504} \\ $$$$\:=\:\mathrm{2}^{\mathrm{4}} ×\mathrm{5}×\mathrm{101}×\mathrm{3}×\mathrm{168} \\ $$$$\:=\:\mathrm{2}^{\mathrm{4}} ×\mathrm{5}×\mathrm{101}×\mathrm{7}×\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{2}} \\ $$$$\:=\:\mathrm{2}^{\mathrm{7}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}×\mathrm{7}×\mathrm{101}\: \\ $$
