
Question Number 22080 by Tinkutara last updated on 10/Oct/17
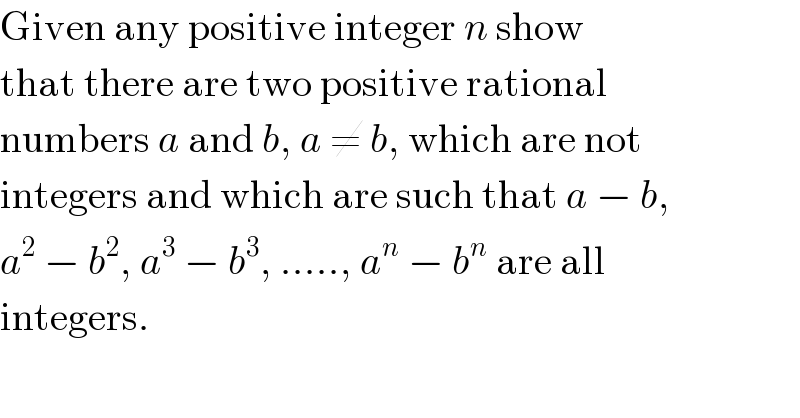
$$\mathrm{Given}\:\mathrm{any}\:\mathrm{positive}\:\mathrm{integer}\:{n}\:\mathrm{show} \\ $$$$\mathrm{that}\:\mathrm{there}\:\mathrm{are}\:\mathrm{two}\:\mathrm{positive}\:\mathrm{rational} \\ $$$$\mathrm{numbers}\:{a}\:\mathrm{and}\:{b},\:{a}\:\neq\:{b},\:\mathrm{which}\:\mathrm{are}\:\mathrm{not} \\ $$$$\mathrm{integers}\:\mathrm{and}\:\mathrm{which}\:\mathrm{are}\:\mathrm{such}\:\mathrm{that}\:{a}\:−\:{b}, \\ $$$${a}^{\mathrm{2}} \:−\:{b}^{\mathrm{2}} ,\:{a}^{\mathrm{3}} \:−\:{b}^{\mathrm{3}} ,\:.....,\:{a}^{{n}} \:−\:{b}^{{n}} \:\mathrm{are}\:\mathrm{all} \\ $$$$\mathrm{integers}. \\ $$
Commented by Rasheed.Sindhi last updated on 11/Oct/17
![For n=2 a−b,a^2 −b^2 ∈Z ⇒ a+b ∈Z [∵ a^2 −b^2 =(a−b)(a+b)] (7/2)−(1/2)=3 ((7/2))^2 −((1/2))^2 =((49)/4)−(1/4)=12 a−b,a+b∈Z⇒a^2 −b^2 ∈Z ;a,b∈Q For n=3 a−b∈Z a^2 −b^2 =(a−b)(a+b)∈Z ⇒a+b∈Z a^3 −b^3 =(a−b)(a^2 +ab+b^2 )∈Z ⇒a^2 +ab+b^2 ∈Z ⋮](Q22106.png)
$$\mathrm{For}\:\mathrm{n}=\mathrm{2} \\ $$$$\:{a}−{b},{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \in\mathbb{Z}\:\Rightarrow\:{a}+{b}\:\in\mathbb{Z} \\ $$$$\:\:\left[\because\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\left({a}−{b}\right)\left({a}+{b}\right)\right] \\ $$$$\frac{\mathrm{7}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{3} \\ $$$$\left(\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{49}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{12} \\ $$$${a}−{b},{a}+{b}\in\mathbb{Z}\Rightarrow{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \in\mathbb{Z}\:;{a},{b}\in\mathbb{Q} \\ $$$$\mathrm{For}\:\mathrm{n}=\mathrm{3} \\ $$$${a}−{b}\in\mathbb{Z} \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\left({a}−{b}\right)\left({a}+{b}\right)\in\mathbb{Z} \\ $$$$\:\Rightarrow{a}+{b}\in\mathbb{Z} \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\left({a}−{b}\right)\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)\in\mathbb{Z} \\ $$$$\:\:\:\Rightarrow{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \in\mathbb{Z} \\ $$$$\vdots \\ $$
