
Question Number 100207 by Rio Michael last updated on 25/Jun/20
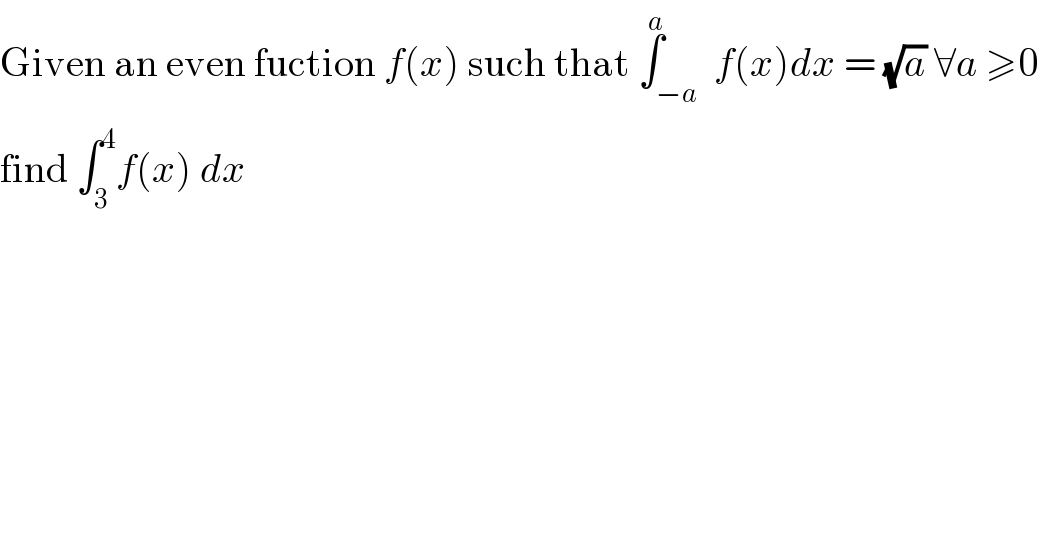
$$\mathrm{Given}\:\mathrm{an}\:\mathrm{even}\:\mathrm{fuction}\:{f}\left({x}\right)\:\mathrm{such}\:\mathrm{that}\:\overset{{a}} {\int}_{−{a}} \:{f}\left({x}\right){dx}\:=\:\sqrt{{a}}\:\forall{a}\:\geqslant\mathrm{0} \\ $$$$\mathrm{find}\:\int_{\mathrm{3}} ^{\mathrm{4}} {f}\left({x}\right)\:{dx} \\ $$$$ \\ $$
Commented by mr W last updated on 25/Jun/20

$$\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}=\frac{\sqrt{{a}}}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} {f}\left({x}\right){dx}=\frac{\sqrt{\mathrm{4}}}{\mathrm{2}}=\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} {f}\left({x}\right){dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\int_{\mathrm{3}} ^{\mathrm{4}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{4}} −\int_{\mathrm{0}} ^{\mathrm{3}} =\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Commented by Rio Michael last updated on 25/Jun/20

$$\mathrm{perfect}\:\mathrm{sir} \\ $$
