
Question Number 3055 by Filup last updated on 04/Dec/15
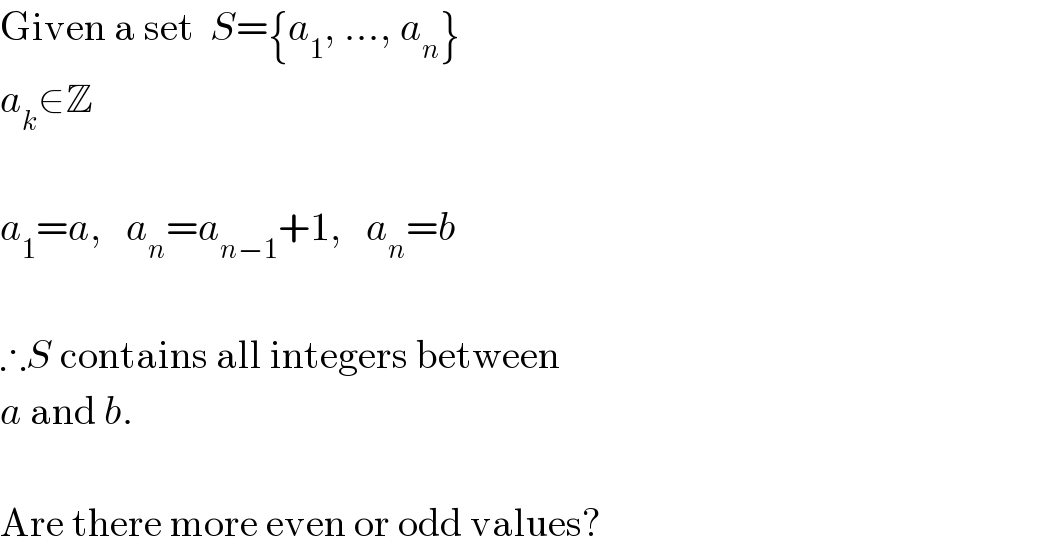
$$\mathrm{Given}\:\mathrm{a}\:\mathrm{set}\:\:{S}=\left\{{a}_{\mathrm{1}} ,\:...,\:{a}_{{n}} \right\} \\ $$$${a}_{{k}} \in\mathbb{Z} \\ $$$$ \\ $$$${a}_{\mathrm{1}} ={a},\:\:\:{a}_{{n}} ={a}_{{n}−\mathrm{1}} +\mathrm{1},\:\:\:{a}_{{n}} ={b} \\ $$$$ \\ $$$$\therefore{S}\:\mathrm{contains}\:\mathrm{all}\:\mathrm{integers}\:\mathrm{between} \\ $$$${a}\:\mathrm{and}\:{b}. \\ $$$$ \\ $$$$\mathrm{Are}\:\mathrm{there}\:\mathrm{more}\:\mathrm{even}\:\mathrm{or}\:\mathrm{odd}\:\mathrm{values}? \\ $$
Answered by 123456 last updated on 04/Dec/15
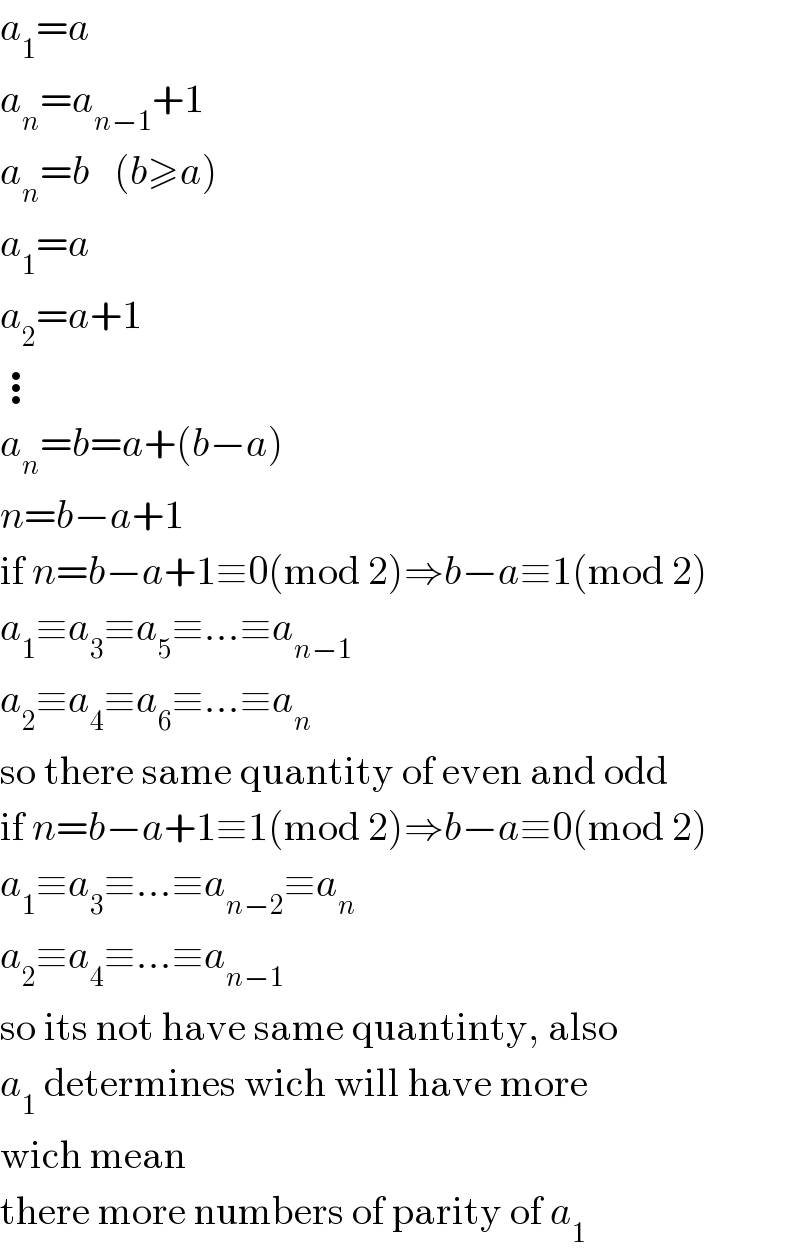
$${a}_{\mathrm{1}} ={a} \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{1}} +\mathrm{1} \\ $$$${a}_{{n}} ={b}\:\:\:\left({b}\geqslant{a}\right) \\ $$$${a}_{\mathrm{1}} ={a} \\ $$$${a}_{\mathrm{2}} ={a}+\mathrm{1} \\ $$$$\vdots \\ $$$${a}_{{n}} ={b}={a}+\left({b}−{a}\right) \\ $$$${n}={b}−{a}+\mathrm{1} \\ $$$$\mathrm{if}\:{n}={b}−{a}+\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}\right)\Rightarrow{b}−{a}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{2}\right) \\ $$$${a}_{\mathrm{1}} \equiv{a}_{\mathrm{3}} \equiv{a}_{\mathrm{5}} \equiv...\equiv{a}_{{n}−\mathrm{1}} \\ $$$${a}_{\mathrm{2}} \equiv{a}_{\mathrm{4}} \equiv{a}_{\mathrm{6}} \equiv...\equiv{a}_{{n}} \\ $$$$\mathrm{so}\:\mathrm{there}\:\mathrm{same}\:\mathrm{quantity}\:\mathrm{of}\:\mathrm{even}\:\mathrm{and}\:\mathrm{odd} \\ $$$$\mathrm{if}\:{n}={b}−{a}+\mathrm{1}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{2}\right)\Rightarrow{b}−{a}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{2}\right) \\ $$$${a}_{\mathrm{1}} \equiv{a}_{\mathrm{3}} \equiv...\equiv{a}_{{n}−\mathrm{2}} \equiv{a}_{{n}} \\ $$$${a}_{\mathrm{2}} \equiv{a}_{\mathrm{4}} \equiv...\equiv{a}_{{n}−\mathrm{1}} \\ $$$$\mathrm{so}\:\mathrm{its}\:\mathrm{not}\:\mathrm{have}\:\mathrm{same}\:\mathrm{quantinty},\:\mathrm{also} \\ $$$${a}_{\mathrm{1}} \:\mathrm{determines}\:\mathrm{wich}\:\mathrm{will}\:\mathrm{have}\:\mathrm{more} \\ $$$$\mathrm{wich}\:\mathrm{mean} \\ $$$$\mathrm{there}\:\mathrm{more}\:\mathrm{numbers}\:\mathrm{of}\:\mathrm{parity}\:\mathrm{of}\:{a}_{\mathrm{1}} \\ $$
Answered by Rasheed Soomro last updated on 04/Dec/15
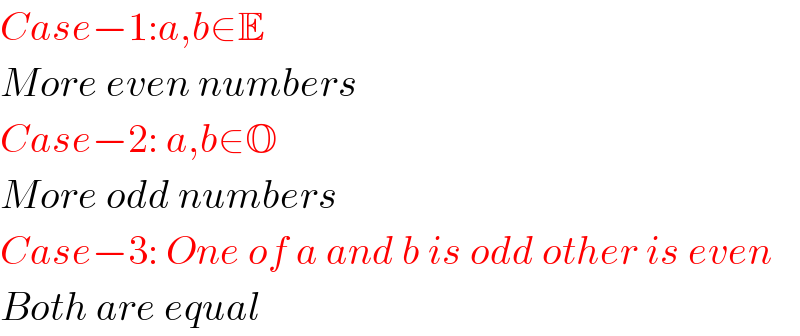
$${Case}−\mathrm{1}:{a},{b}\in\mathbb{E} \\ $$$${More}\:{even}\:{numbers} \\ $$$${Case}−\mathrm{2}:\:{a},{b}\in\mathbb{O} \\ $$$${More}\:{odd}\:{numbers} \\ $$$${Case}−\mathrm{3}:\:{One}\:{of}\:{a}\:{and}\:{b}\:{is}\:{odd}\:{other}\:{is}\:{even} \\ $$$${Both}\:{are}\:{equal} \\ $$
