Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 217190 by efronzo1 last updated on 05/Mar/25

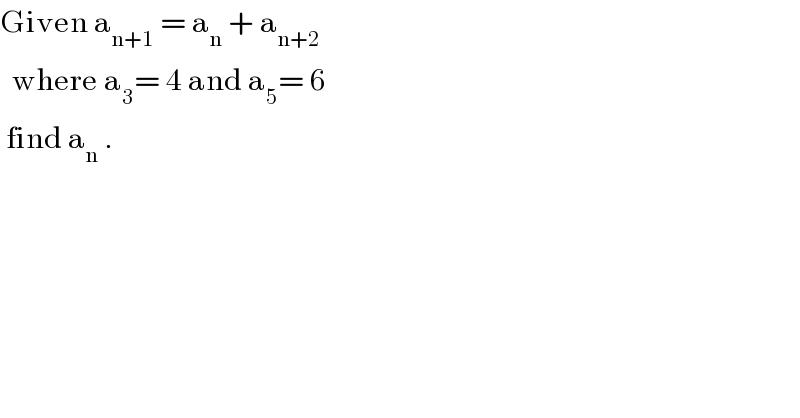
Given a_(n+1) = a_n + a_(n+2) where a_3 = 4 and a_5 = 6 find a_n .

$$\mathrm{Given}\:\mathrm{a}_{\mathrm{n}+\mathrm{1}} \:=\:\mathrm{a}_{\mathrm{n}} \:+\:\mathrm{a}_{\mathrm{n}+\mathrm{2}} \: \\ $$$$\:\:\mathrm{where}\:\mathrm{a}_{\mathrm{3}} =\:\mathrm{4}\:\mathrm{and}\:\mathrm{a}_{\mathrm{5}} =\:\mathrm{6} \\ $$$$\:\mathrm{find}\:\mathrm{a}_{\mathrm{n}} \:. \\ $$

Answered by mr W last updated on 05/Mar/25

a_(n+2) −a_(n+1) +a_n =0 characteristic equation: r^2 −r+1=0 ⇒r_(1,2) =((1±i(√3))/2)=e^(±((πi)/3)) say a_n =Ae^((nπi)/3) +Be^(−((nπi)/3)) or a_n =C cos ((nπ)/3)+D sin ((nπ)/3) a_3 =−C=4 ⇒C=−4 a_5 =−4 cos ((5π)/3)+D sin ((5π)/3)=6 ⇒D=−((16)/( (√3))) ⇒a_n =−4(cos ((nπ)/3)+(4/( (√3))) sin ((nπ)/3)) or a_n =−((4(√(57)))/( 3)) sin (((nπ)/3)+tan^(−1) ((√3)/4))

$${a}_{{n}+\mathrm{2}} −{a}_{{n}+\mathrm{1}} +{a}_{{n}} =\mathrm{0} \\ $$$${characteristic}\:{equation}: \\ $$$${r}^{\mathrm{2}} −{r}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{r}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{\pm\frac{\pi{i}}{\mathrm{3}}} \\ $$$${say}\:{a}_{{n}} ={Ae}^{\frac{{n}\pi{i}}{\mathrm{3}}} +{Be}^{−\frac{{n}\pi{i}}{\mathrm{3}}} \\ $$$${or}\:{a}_{{n}} ={C}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}}+{D}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}} \\ $$$${a}_{\mathrm{3}} =−{C}=\mathrm{4}\:\Rightarrow{C}=−\mathrm{4} \\ $$$${a}_{\mathrm{5}} =−\mathrm{4}\:\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{3}}+{D}\:\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{3}}=\mathrm{6}\:\Rightarrow{D}=−\frac{\mathrm{16}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{a}_{{n}} =−\mathrm{4}\left(\mathrm{cos}\:\frac{{n}\pi}{\mathrm{3}}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{3}}\right) \\ $$$${or} \\ $$$${a}_{{n}} =−\frac{\mathrm{4}\sqrt{\mathrm{57}}}{\:\mathrm{3}}\:\mathrm{sin}\:\left(\frac{{n}\pi}{\mathrm{3}}+\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com