Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 179090 by CrispyXYZ last updated on 24/Oct/22

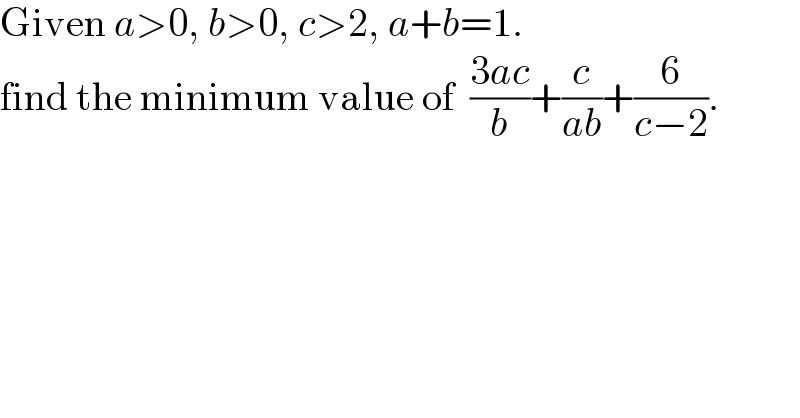
Given a>0, b>0, c>2, a+b=1. find the minimum value of ((3ac)/b)+(c/(ab))+(6/(c−2)).

$$\mathrm{Given}\:{a}>\mathrm{0},\:{b}>\mathrm{0},\:{c}>\mathrm{2},\:{a}+{b}=\mathrm{1}. \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\:\frac{\mathrm{3}{ac}}{{b}}+\frac{{c}}{{ab}}+\frac{\mathrm{6}}{{c}−\mathrm{2}}. \\ $$

Commented by Frix last updated on 24/Oct/22

24

$$\mathrm{24} \\ $$

Answered by MJS_new last updated on 24/Oct/22

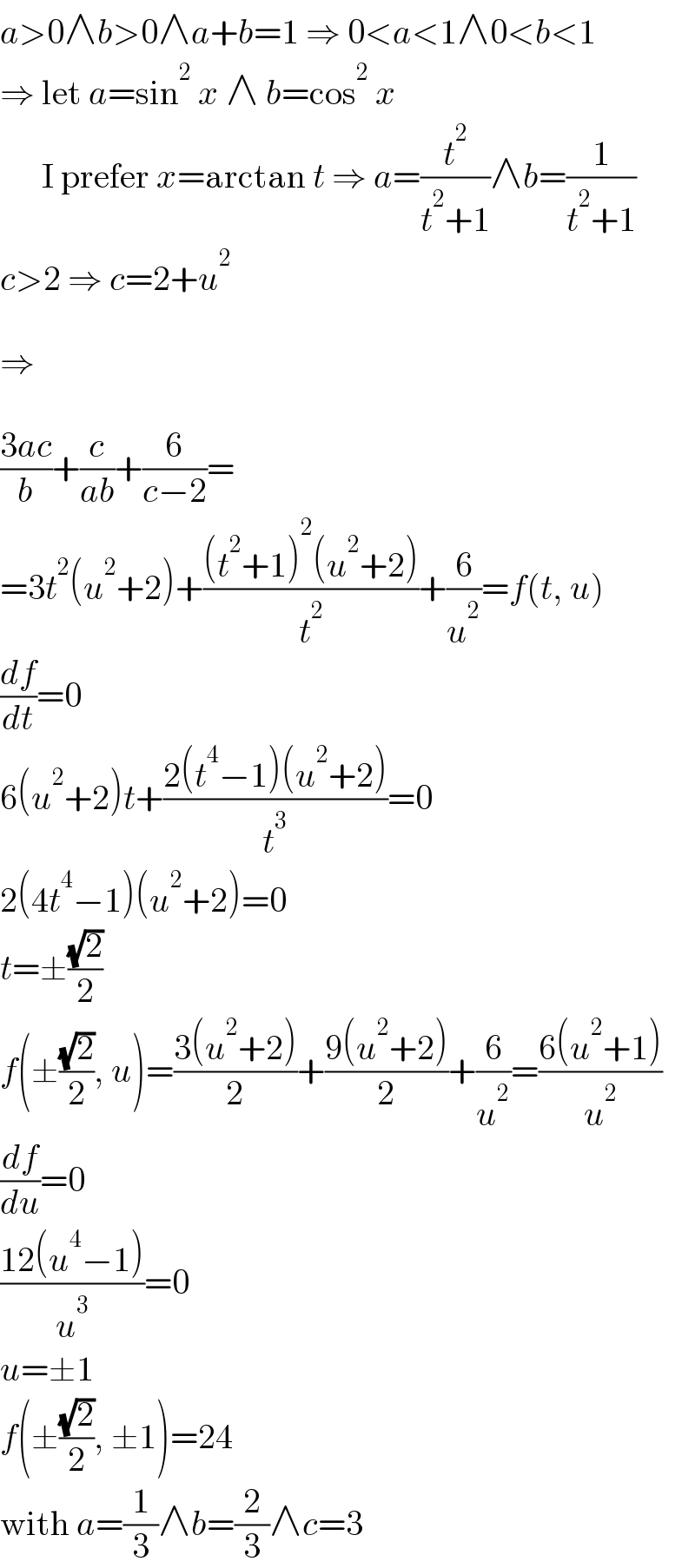
a>0∧b>0∧a+b=1 ⇒ 0<a<1∧0<b<1 ⇒ let a=sin^2 x ∧ b=cos^2 x I prefer x=arctan t ⇒ a=(t^2 /(t^2 +1))∧b=(1/(t^2 +1)) c>2 ⇒ c=2+u^2 ⇒ ((3ac)/b)+(c/(ab))+(6/(c−2))= =3t^2 (u^2 +2)+(((t^2 +1)^2 (u^2 +2))/t^2 )+(6/u^2 )=f(t, u) (df/dt)=0 6(u^2 +2)t+((2(t^4 −1)(u^2 +2))/t^3 )=0 2(4t^4 −1)(u^2 +2)=0 t=±((√2)/2) f(±((√2)/2), u)=((3(u^2 +2))/2)+((9(u^2 +2))/2)+(6/u^2 )=((6(u^2 +1))/u^2 ) (df/du)=0 ((12(u^4 −1))/u^3 )=0 u=±1 f(±((√2)/2), ±1)=24 with a=(1/3)∧b=(2/3)∧c=3

$${a}>\mathrm{0}\wedge{b}>\mathrm{0}\wedge{a}+{b}=\mathrm{1}\:\Rightarrow\:\mathrm{0}<{a}<\mathrm{1}\wedge\mathrm{0}<{b}<\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{let}\:{a}=\mathrm{sin}^{\mathrm{2}} \:{x}\:\wedge\:{b}=\mathrm{cos}^{\mathrm{2}} \:{x} \\ $$$$\:\:\:\:\:\:\mathrm{I}\:\mathrm{prefer}\:{x}=\mathrm{arctan}\:{t}\:\Rightarrow\:{a}=\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}\wedge{b}=\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${c}>\mathrm{2}\:\Rightarrow\:{c}=\mathrm{2}+{u}^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow \\ $$$$ \\ $$$$\frac{\mathrm{3}{ac}}{{b}}+\frac{{c}}{{ab}}+\frac{\mathrm{6}}{{c}−\mathrm{2}}= \\ $$$$=\mathrm{3}{t}^{\mathrm{2}} \left({u}^{\mathrm{2}} +\mathrm{2}\right)+\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({u}^{\mathrm{2}} +\mathrm{2}\right)}{{t}^{\mathrm{2}} }+\frac{\mathrm{6}}{{u}^{\mathrm{2}} }={f}\left({t},\:{u}\right) \\ $$$$\frac{{df}}{{dt}}=\mathrm{0} \\ $$$$\mathrm{6}\left({u}^{\mathrm{2}} +\mathrm{2}\right){t}+\frac{\mathrm{2}\left({t}^{\mathrm{4}} −\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{2}\right)}{{t}^{\mathrm{3}} }=\mathrm{0} \\ $$$$\mathrm{2}\left(\mathrm{4}{t}^{\mathrm{4}} −\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{0} \\ $$$${t}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${f}\left(\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\:{u}\right)=\frac{\mathrm{3}\left({u}^{\mathrm{2}} +\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{9}\left({u}^{\mathrm{2}} +\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{6}}{{u}^{\mathrm{2}} }=\frac{\mathrm{6}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{{u}^{\mathrm{2}} } \\ $$$$\frac{{df}}{{du}}=\mathrm{0} \\ $$$$\frac{\mathrm{12}\left({u}^{\mathrm{4}} −\mathrm{1}\right)}{{u}^{\mathrm{3}} }=\mathrm{0} \\ $$$${u}=\pm\mathrm{1} \\ $$$${f}\left(\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\:\pm\mathrm{1}\right)=\mathrm{24} \\ $$$$\mathrm{with}\:{a}=\frac{\mathrm{1}}{\mathrm{3}}\wedge{b}=\frac{\mathrm{2}}{\mathrm{3}}\wedge{c}=\mathrm{3} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com