Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 124007 by liberty last updated on 30/Nov/20

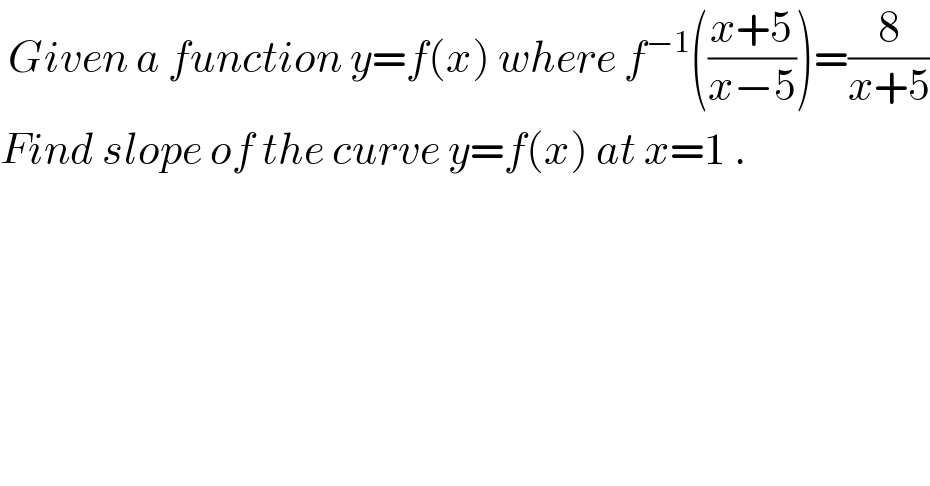
Given a function y=f(x) where f^(−1) (((x+5)/(x−5)))=(8/(x+5)) Find slope of the curve y=f(x) at x=1 .

$$\:{Given}\:{a}\:{function}\:{y}={f}\left({x}\right)\:{where}\:{f}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{5}}\right)=\frac{\mathrm{8}}{{x}+\mathrm{5}} \\ $$$${Find}\:{slope}\:{of}\:{the}\:{curve}\:{y}={f}\left({x}\right)\:{at}\:{x}=\mathrm{1}\:. \\ $$

Answered by john_santu last updated on 30/Nov/20

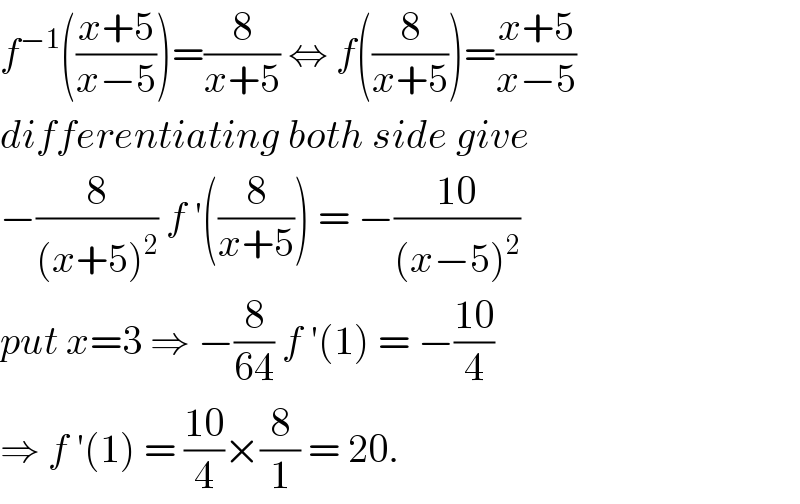
f^(−1) (((x+5)/(x−5)))=(8/(x+5)) ⇔ f((8/(x+5)))=((x+5)/(x−5)) differentiating both side give −(8/((x+5)^2 )) f ′((8/(x+5))) = −((10)/((x−5)^2 )) put x=3 ⇒ −(8/(64)) f ′(1) = −((10)/4) ⇒ f ′(1) = ((10)/4)×(8/1) = 20.

$${f}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{5}}\right)=\frac{\mathrm{8}}{{x}+\mathrm{5}}\:\Leftrightarrow\:{f}\left(\frac{\mathrm{8}}{{x}+\mathrm{5}}\right)=\frac{{x}+\mathrm{5}}{{x}−\mathrm{5}} \\ $$$${differentiating}\:{both}\:{side}\:{give} \\ $$$$−\frac{\mathrm{8}}{\left({x}+\mathrm{5}\right)^{\mathrm{2}} }\:{f}\:'\left(\frac{\mathrm{8}}{{x}+\mathrm{5}}\right)\:=\:−\frac{\mathrm{10}}{\left({x}−\mathrm{5}\right)^{\mathrm{2}} } \\ $$$${put}\:{x}=\mathrm{3}\:\Rightarrow\:−\frac{\mathrm{8}}{\mathrm{64}}\:{f}\:'\left(\mathrm{1}\right)\:=\:−\frac{\mathrm{10}}{\mathrm{4}} \\ $$$$\Rightarrow\:{f}\:'\left(\mathrm{1}\right)\:=\:\frac{\mathrm{10}}{\mathrm{4}}×\frac{\mathrm{8}}{\mathrm{1}}\:=\:\mathrm{20}.\: \\ $$

Answered by mathmax by abdo last updated on 30/Nov/20

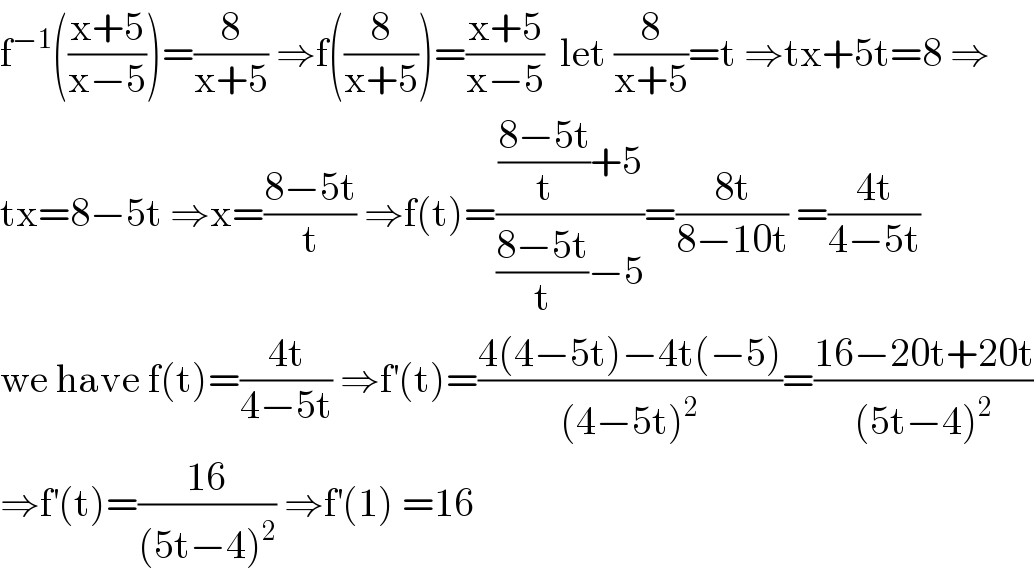
f^(−1) (((x+5)/(x−5)))=(8/(x+5)) ⇒f((8/(x+5)))=((x+5)/(x−5)) let (8/(x+5))=t ⇒tx+5t=8 ⇒ tx=8−5t ⇒x=((8−5t)/t) ⇒f(t)=((((8−5t)/t)+5)/(((8−5t)/t)−5))=((8t)/(8−10t)) =((4t)/(4−5t)) we have f(t)=((4t)/(4−5t)) ⇒f^′ (t)=((4(4−5t)−4t(−5))/((4−5t)^2 ))=((16−20t+20t)/((5t−4)^2 )) ⇒f^′ (t)=((16)/((5t−4)^2 )) ⇒f^′ (1) =16

$$\mathrm{f}^{−\mathrm{1}} \left(\frac{\mathrm{x}+\mathrm{5}}{\mathrm{x}−\mathrm{5}}\right)=\frac{\mathrm{8}}{\mathrm{x}+\mathrm{5}}\:\Rightarrow\mathrm{f}\left(\frac{\mathrm{8}}{\mathrm{x}+\mathrm{5}}\right)=\frac{\mathrm{x}+\mathrm{5}}{\mathrm{x}−\mathrm{5}}\:\:\mathrm{let}\:\frac{\mathrm{8}}{\mathrm{x}+\mathrm{5}}=\mathrm{t}\:\Rightarrow\mathrm{tx}+\mathrm{5t}=\mathrm{8}\:\Rightarrow \\ $$$$\mathrm{tx}=\mathrm{8}−\mathrm{5t}\:\Rightarrow\mathrm{x}=\frac{\mathrm{8}−\mathrm{5t}}{\mathrm{t}}\:\Rightarrow\mathrm{f}\left(\mathrm{t}\right)=\frac{\frac{\mathrm{8}−\mathrm{5t}}{\mathrm{t}}+\mathrm{5}}{\frac{\mathrm{8}−\mathrm{5t}}{\mathrm{t}}−\mathrm{5}}=\frac{\mathrm{8t}}{\mathrm{8}−\mathrm{10t}}\:=\frac{\mathrm{4t}}{\mathrm{4}−\mathrm{5t}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{t}\right)=\frac{\mathrm{4t}}{\mathrm{4}−\mathrm{5t}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{t}\right)=\frac{\mathrm{4}\left(\mathrm{4}−\mathrm{5t}\right)−\mathrm{4t}\left(−\mathrm{5}\right)}{\left(\mathrm{4}−\mathrm{5t}\right)^{\mathrm{2}} }=\frac{\mathrm{16}−\mathrm{20t}+\mathrm{20t}}{\left(\mathrm{5t}−\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{t}\right)=\frac{\mathrm{16}}{\left(\mathrm{5t}−\mathrm{4}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{1}\right)\:=\mathrm{16} \\ $$

Commented by liberty last updated on 30/Nov/20

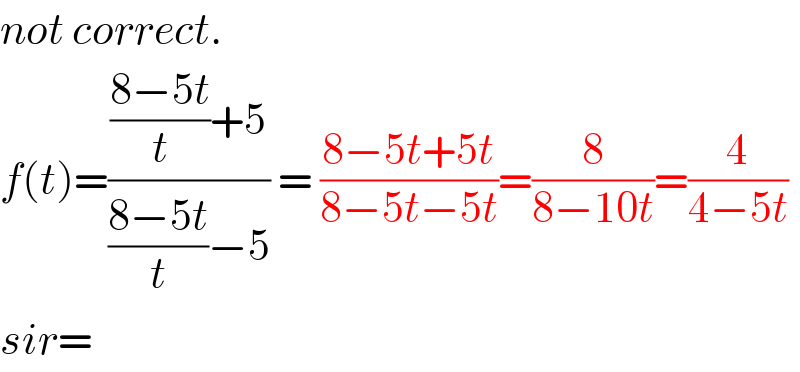
not correct. f(t)=((((8−5t)/t)+5)/(((8−5t)/t)−5)) = ((8−5t+5t)/(8−5t−5t))=(8/(8−10t))=(4/(4−5t)) sir=

$${not}\:{correct}. \\ $$$${f}\left({t}\right)=\frac{\frac{\mathrm{8}−\mathrm{5}{t}}{{t}}+\mathrm{5}}{\frac{\mathrm{8}−\mathrm{5}{t}}{{t}}−\mathrm{5}}\:=\:\frac{\mathrm{8}−\mathrm{5}{t}+\mathrm{5}{t}}{\mathrm{8}−\mathrm{5}{t}−\mathrm{5}{t}}=\frac{\mathrm{8}}{\mathrm{8}−\mathrm{10}{t}}=\frac{\mathrm{4}}{\mathrm{4}−\mathrm{5}{t}} \\ $$$${sir}= \\ $$

Commented by Bird last updated on 30/Nov/20

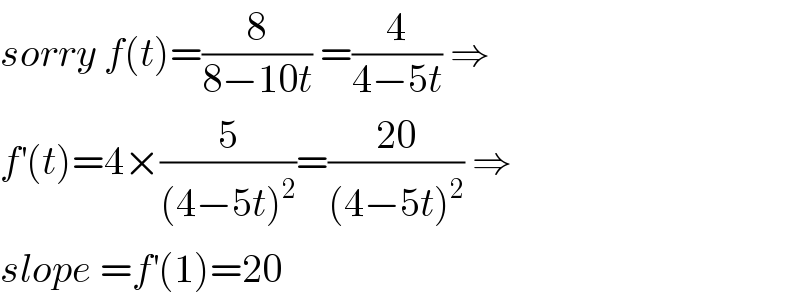
sorry f(t)=(8/(8−10t)) =(4/(4−5t)) ⇒ f^′ (t)=4×(5/((4−5t)^2 ))=((20)/((4−5t)^2 )) ⇒ slope =f^′ (1)=20

$${sorry}\:{f}\left({t}\right)=\frac{\mathrm{8}}{\mathrm{8}−\mathrm{10}{t}}\:=\frac{\mathrm{4}}{\mathrm{4}−\mathrm{5}{t}}\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)=\mathrm{4}×\frac{\mathrm{5}}{\left(\mathrm{4}−\mathrm{5}{t}\right)^{\mathrm{2}} }=\frac{\mathrm{20}}{\left(\mathrm{4}−\mathrm{5}{t}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${slope}\:={f}^{'} \left(\mathrm{1}\right)=\mathrm{20} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com