
Question Number 114181 by bemath last updated on 17/Sep/20
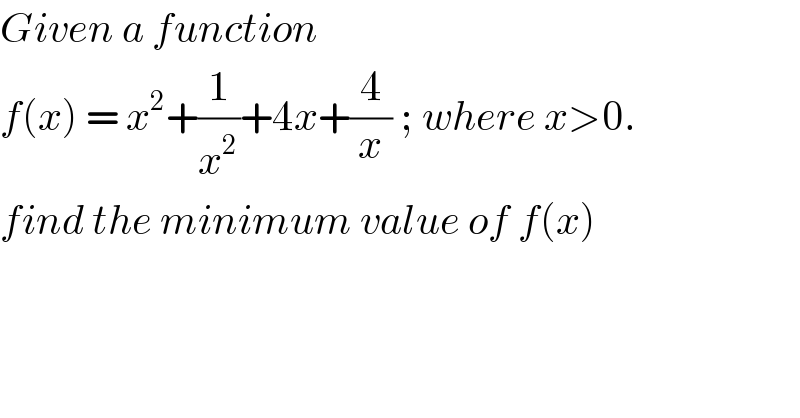
$${Given}\:{a}\:{function}\: \\ $$$${f}\left({x}\right)\:=\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{4}{x}+\frac{\mathrm{4}}{{x}}\:;\:{where}\:{x}>\mathrm{0}. \\ $$$${find}\:{the}\:{minimum}\:{value}\:{of}\:{f}\left({x}\right) \\ $$
Answered by bobhans last updated on 17/Sep/20
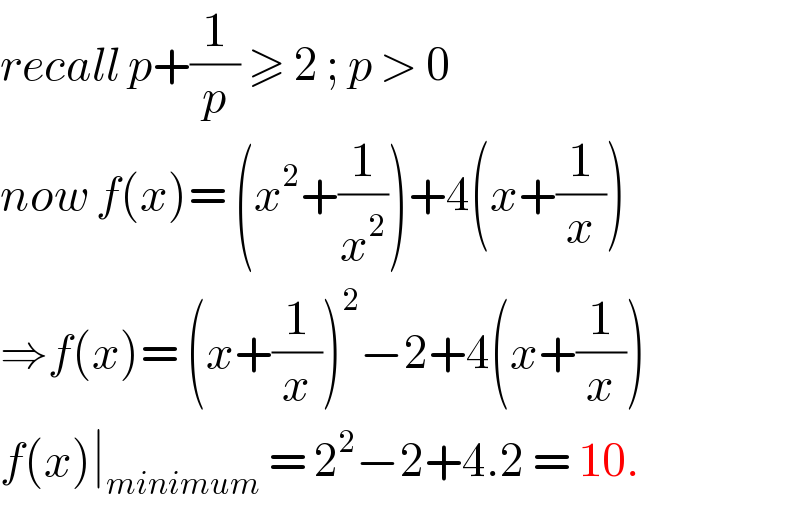
$${recall}\:{p}+\frac{\mathrm{1}}{{p}}\:\geqslant\:\mathrm{2}\:;\:{p}\:>\:\mathrm{0} \\ $$$${now}\:{f}\left({x}\right)=\:\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)+\mathrm{4}\left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$$\Rightarrow{f}\left({x}\right)=\:\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}+\mathrm{4}\left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${f}\left({x}\right)\mid_{{minimum}} \:=\:\mathrm{2}^{\mathrm{2}} −\mathrm{2}+\mathrm{4}.\mathrm{2}\:=\:\mathrm{10}. \\ $$
Answered by mathmax by abdo last updated on 17/Sep/20
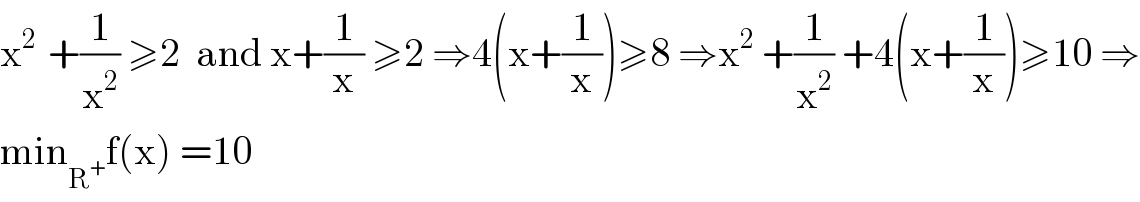
$$\mathrm{x}^{\mathrm{2}\:} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:\geqslant\mathrm{2}\:\:\mathrm{and}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\:\geqslant\mathrm{2}\:\Rightarrow\mathrm{4}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)\geqslant\mathrm{8}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:+\mathrm{4}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)\geqslant\mathrm{10}\:\Rightarrow \\ $$$$\mathrm{min}_{\mathrm{R}^{+} } \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{10} \\ $$
Answered by 1549442205PVT last updated on 18/Sep/20
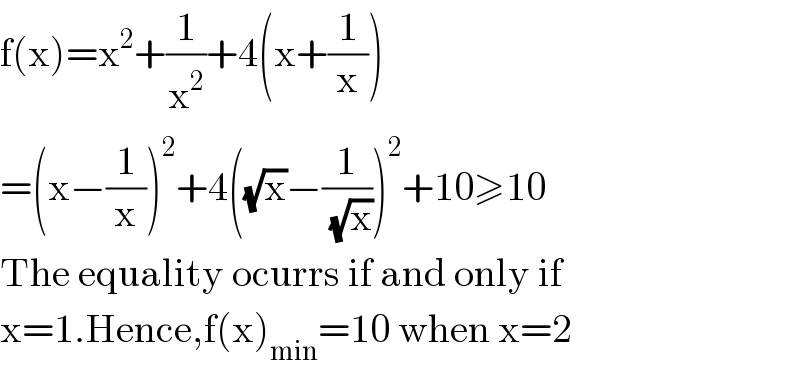
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{4}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$=\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{4}\left(\sqrt{\mathrm{x}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}}\right)^{\mathrm{2}} +\mathrm{10}\geqslant\mathrm{10} \\ $$$$\mathrm{The}\:\mathrm{equality}\:\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if} \\ $$$$\mathrm{x}=\mathrm{1}.\mathrm{Hence},\mathrm{f}\left(\mathrm{x}\right)_{\mathrm{min}} =\mathrm{10}\:\mathrm{when}\:\mathrm{x}=\mathrm{2} \\ $$
