
Question Number 125099 by bramlexs22 last updated on 08/Dec/20
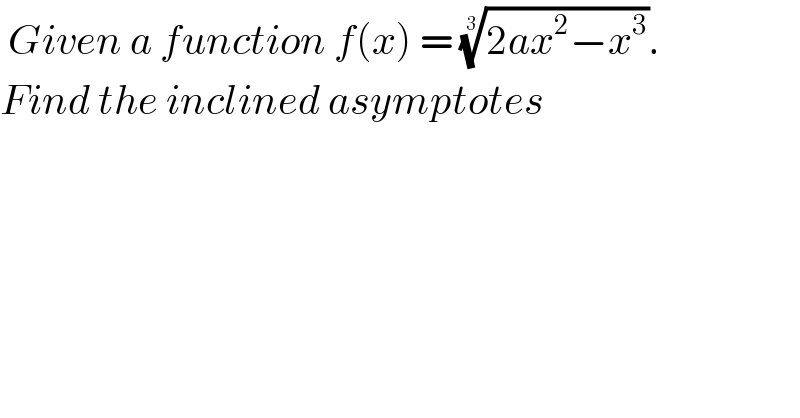
$$\:{Given}\:{a}\:{function}\:{f}\left({x}\right)\:=\:\sqrt[{\mathrm{3}}]{\mathrm{2}{ax}^{\mathrm{2}} −{x}^{\mathrm{3}} }. \\ $$$${Find}\:{the}\:{inclined}\:{asymptotes} \\ $$
Answered by liberty last updated on 08/Dec/20
![k = lim_(x→±∞) (y/x) = lim_(x→±∞) (((2ax^2 −x^3 ))^(1/3) /x) lim_(x→±∞) ((((2a)/x)−1))^(1/3) = −1 b =lim_(x→±∞) [y−kx ] = lim_(x→±∞) [ ((2ax^2 −x^3 ))^(1/3) + x ] = lim_(x→±∞) ((2ax^2 −x^3 +x^3 )/( (((2ax^2 −x^3 )^2 ))^(1/3) −x ((2ax^2 −x^3 ))^(1/3) +x^2 )) = lim_(x→±∞) ((2ax^2 )/( (((2ax^2 −x^3 )^2 ))^(1/3) −x ((2ax^2 −x^3 ))^(1/3) +x^2 )) = ((2a)/3) thus the straight line y=−x+((2a)/3) is a inclined asymptotes to the curve y =((2ax^2 −x^3 ))^(1/3) .](Q125100.png)
$$\:{k}\:=\:\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\:\frac{{y}}{{x}}\:=\:\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}{ax}^{\mathrm{2}} −{x}^{\mathrm{3}} }}{{x}}\: \\ $$$$\:\:\:\:\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}{a}}{{x}}−\mathrm{1}}\:=\:−\mathrm{1} \\ $$$$\:{b}\:=\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\:\left[{y}−{kx}\:\right]\:=\:\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\left[\:\sqrt[{\mathrm{3}}]{\mathrm{2}{ax}^{\mathrm{2}} −{x}^{\mathrm{3}} \:}\:+\:{x}\:\right] \\ $$$$\:\:=\:\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\:\frac{\mathrm{2}{ax}^{\mathrm{2}} −{x}^{\mathrm{3}} +{x}^{\mathrm{3}} }{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{2}{ax}^{\mathrm{2}} −{x}^{\mathrm{3}} \right)^{\mathrm{2}} }−{x}\:\sqrt[{\mathrm{3}}]{\mathrm{2}{ax}^{\mathrm{2}} −{x}^{\mathrm{3}} }\:+{x}^{\mathrm{2}} } \\ $$$$\:\:=\:\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\frac{\mathrm{2}{ax}^{\mathrm{2}} }{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{2}{ax}^{\mathrm{2}} −{x}^{\mathrm{3}} \right)^{\mathrm{2}} }−{x}\:\sqrt[{\mathrm{3}}]{\mathrm{2}{ax}^{\mathrm{2}} −{x}^{\mathrm{3}} }+{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}{a}}{\mathrm{3}} \\ $$$${thus}\:{the}\:{straight}\:{line}\:{y}=−{x}+\frac{\mathrm{2}{a}}{\mathrm{3}}\:{is}\:{a}\:{inclined} \\ $$$${asymptotes}\:{to}\:{the}\:{curve}\:{y}\:=\sqrt[{\mathrm{3}}]{\mathrm{2}{ax}^{\mathrm{2}} −{x}^{\mathrm{3}} }\:. \\ $$
Commented by bramlexs22 last updated on 08/Dec/20

$${thanks}\:{a}\:{lot}\: \\ $$
