
Question Number 105356 by bemath last updated on 28/Jul/20
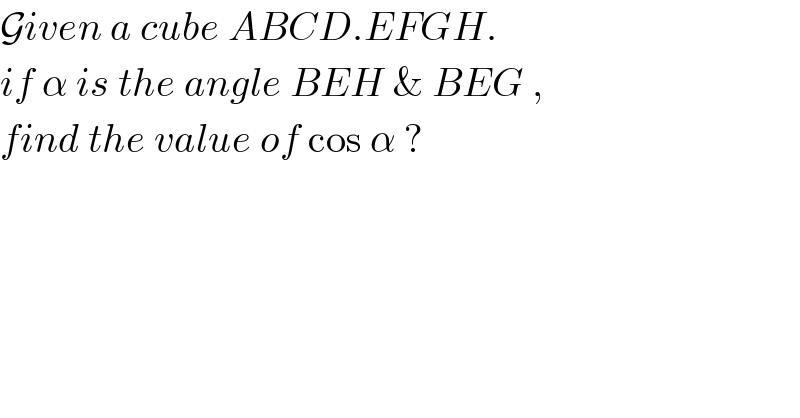
$$\mathcal{G}{iven}\:{a}\:{cube}\:{ABCD}.{EFGH}. \\ $$$${if}\:\alpha\:{is}\:{the}\:{angle}\:{BEH}\:\&\:{BEG}\:, \\ $$$${find}\:{the}\:{value}\:{of}\:\mathrm{cos}\:\alpha\:? \\ $$
Answered by john santu last updated on 28/Jul/20

Commented by john santu last updated on 28/Jul/20

$${with}\:{normal}\:{vector}\:\overset{\rightarrow} {{n}}_{\mathrm{1}} \:\&\:\overset{\rightarrow} {{n}}_{\mathrm{2}} \\ $$$$\overset{\rightarrow} {{n}}_{\mathrm{1}} =\begin{vmatrix}{−\mathrm{2}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:−\mathrm{2}}\end{vmatrix}=\left(\mathrm{0},−\mathrm{4},−\mathrm{4}\right)\: \\ $$$$\overset{\rightarrow} {{n}}_{\mathrm{2}} =\:\begin{vmatrix}{\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:−\mathrm{2}}\\{−\mathrm{2}\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\mathrm{0}}\end{vmatrix}=\left(\mathrm{4},\mathrm{4},\mathrm{4}\right) \\ $$$$\mathrm{cos}\:\alpha\:=\:\frac{\mid\overset{\rightarrow} {{n}}_{\mathrm{1}} \circ\overset{\rightarrow} {{n}}_{\mathrm{2}} \mid}{\mid\overset{\rightarrow} {{n}}_{\mathrm{1}} \mid.\mid\overset{\rightarrow} {{n}}_{\mathrm{2}} \mid}\:=\:\frac{\mathrm{32}}{\mathrm{4}\sqrt{\mathrm{2}}\:.\mathrm{4}\sqrt{\mathrm{3}}}\:=\:\frac{\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\left({JS}\:\spadesuit\blacklozenge\right)\: \\ $$
Commented by bemath last updated on 28/Jul/20

$${great}.. \\ $$
