Question and Answers Forum

All Questions      Topic List

Operation Research Questions

Previous in All Question      Next in All Question      

Previous in Operation Research      

Question Number 217769 by nECxx2 last updated on 20/Mar/25

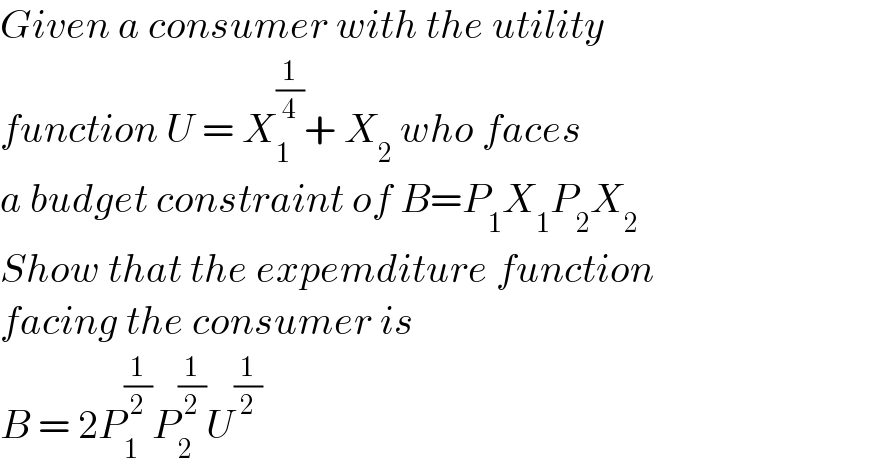
Given a consumer with the utility function U = X_1 ^(1/4) + X_2 who faces a budget constraint of B=P_1 X_1 P_2 X_2 Show that the expemditure function facing the consumer is B = 2P_1 ^(1/2) P_2 ^(1/2) U^(1/2)

$${Given}\:{a}\:{consumer}\:{with}\:{the}\:{utility} \\ $$$${function}\:{U}\:=\:{X}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{4}}} +\:{X}_{\mathrm{2}} \:{who}\:{faces} \\ $$$${a}\:{budget}\:{constraint}\:{of}\:{B}={P}_{\mathrm{1}} {X}_{\mathrm{1}} {P}_{\mathrm{2}} {X}_{\mathrm{2}} \\ $$$${Show}\:{that}\:{the}\:{expemditure}\:{function} \\ $$$${facing}\:{the}\:{consumer}\:{is} \\ $$$${B}\:=\:\mathrm{2}{P}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {P}_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {U}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$

Commented by nECxx2 last updated on 20/Mar/25

Please help

$${Please}\:{help} \\ $$

Answered by MrGaster last updated on 21/Mar/25

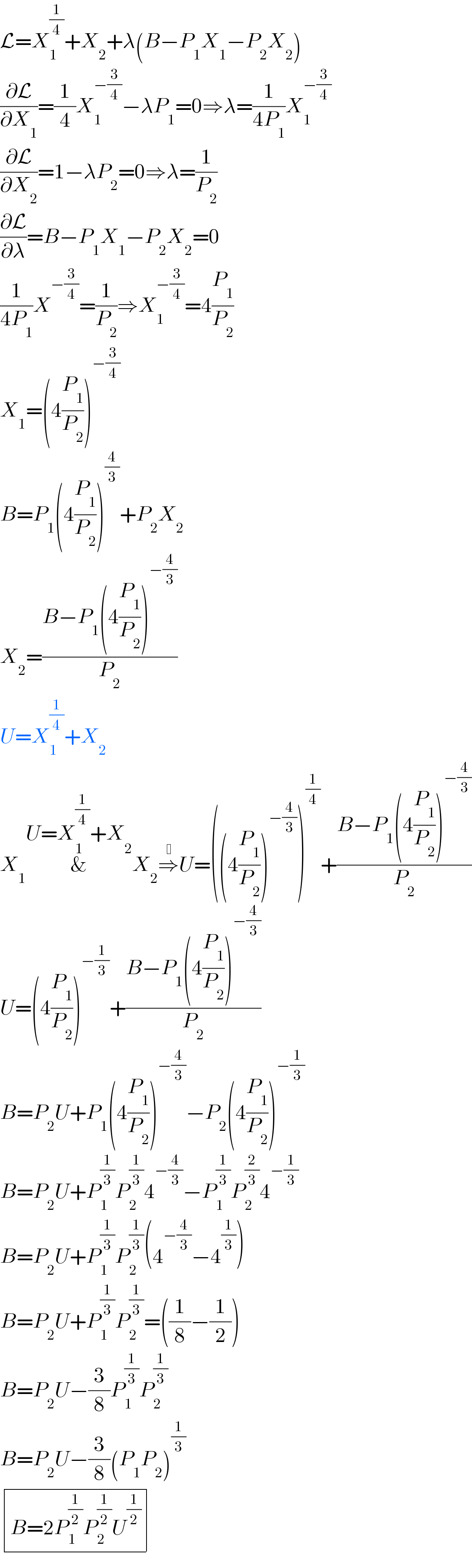
L=X_1 ^(1/4) +X_2 +λ(B−P_1 X_1 −P_2 X_2 ) (∂L/∂X_1 )=(1/4)X_1 ^(−(3/4)) −λP_1 =0⇒λ=(1/(4P_1 ))X_1 ^(−(3/4)) (∂L/∂X_2 )=1−λP_2 =0⇒λ=(1/P_2 ) (∂L/∂λ)=B−P_1 X_1 −P_2 X_2 =0 (1/(4P_1 ))X^(−(3/4)) =(1/P_2 )⇒X_1 ^(−(3/4)) =4(P_1 /P_2 ) X_1 =(4(P_1 /P_2 ))^(−(3/4)) B=P_1 (4(P_1 /P_2 ))^(4/3) +P_2 X_2 X_2 =((B−P_1 (4(P_1 /P_2 ))^(−(4/3)) )/P_2 ) U=X_1 ^(1/4) +X_2 X_1 &^(U=X_1 ^(1/4) +X_2 ) X_2 ⇒^( ) U=((4(P_1 /P_2 ))^(−(4/3)) )^(1/4) +((B−P_1 (4(P_1 /P_2 ))^(−(4/3)) )/P_2 ) U=(4(P_1 /P_2 ))^(−(1/3)) +((B−P_1 (4(P_1 /P_2 ))^(−(4/3)) )/P_2 ) B=P_2 U+P_1 (4(P_1 /P_2 ))^(−(4/3)) −P_2 (4(P_1 /P_2 ))^(−(1/3)) B=P_2 U+P_1 ^(1/3) P_2 ^(1/3) 4^(−(4/3)) −P_1 ^(1/3) P_2 ^(2/3) 4^(−(1/3)) B=P_2 U+P_1 ^(1/3) P_2 ^(1/3) (4^(−(4/3)) −4^(1/3) ) B=P_2 U+P_1 ^(1/3) P_2 ^(1/3) =((1/8)−(1/2)) B=P_2 U−(3/8)P_1 ^(1/3) P_2 ^(1/3) B=P_2 U−(3/8)(P_1 P_2 )^(1/3) determinant (((B=2P_1 ^(1/2) P_2 ^(1/2) U^(1/2) )))

$$\mathcal{L}={X}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{4}}} +{X}_{\mathrm{2}} +\lambda\left({B}−{P}_{\mathrm{1}} {X}_{\mathrm{1}} −{P}_{\mathrm{2}} {X}_{\mathrm{2}} \right) \\ $$$$\frac{\partial\mathcal{L}}{\partial{X}_{\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{4}}{X}_{\mathrm{1}} ^{−\frac{\mathrm{3}}{\mathrm{4}}} −\lambda{P}_{\mathrm{1}} =\mathrm{0}\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{4}{P}_{\mathrm{1}} }{X}_{\mathrm{1}} ^{−\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\frac{\partial\mathcal{L}}{\partial{X}_{\mathrm{2}} }=\mathrm{1}−\lambda{P}_{\mathrm{2}} =\mathrm{0}\Rightarrow\lambda=\frac{\mathrm{1}}{{P}_{\mathrm{2}} } \\ $$$$\frac{\partial\mathcal{L}}{\partial\lambda}={B}−{P}_{\mathrm{1}} {X}_{\mathrm{1}} −{P}_{\mathrm{2}} {X}_{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{P}_{\mathrm{1}} }{X}^{−\frac{\mathrm{3}}{\mathrm{4}}} =\frac{\mathrm{1}}{{P}_{\mathrm{2}} }\Rightarrow{X}_{\mathrm{1}} ^{−\frac{\mathrm{3}}{\mathrm{4}}} =\mathrm{4}\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} } \\ $$$${X}_{\mathrm{1}} =\left(\mathrm{4}\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }\right)^{−\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$${B}={P}_{\mathrm{1}} \left(\mathrm{4}\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }\right)^{\frac{\mathrm{4}}{\mathrm{3}}} +{P}_{\mathrm{2}} {X}_{\mathrm{2}} \\ $$$${X}_{\mathrm{2}} =\frac{{B}−{P}_{\mathrm{1}} \left(\mathrm{4}\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }\right)^{−\frac{\mathrm{4}}{\mathrm{3}}} }{{P}_{\mathrm{2}} } \\ $$$${U}={X}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{4}}} +{X}_{\mathrm{2}} \\ $$$${X}_{\mathrm{1}} \overset{{U}={X}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{4}}} +{X}_{\mathrm{2}} } {\&}{X}_{\mathrm{2}} \overset{\: } {\Rightarrow}{U}=\left(\left(\mathrm{4}\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }\right)^{−\frac{\mathrm{4}}{\mathrm{3}}} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} +\frac{{B}−{P}_{\mathrm{1}} \left(\mathrm{4}\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }\right)^{−\frac{\mathrm{4}}{\mathrm{3}}} }{{P}_{\mathrm{2}} } \\ $$$${U}=\left(\mathrm{4}\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }\right)^{−\frac{\mathrm{1}}{\mathrm{3}}} +\frac{{B}−{P}_{\mathrm{1}} \left(\mathrm{4}\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }\right)^{−\frac{\mathrm{4}}{\mathrm{3}}} }{{P}_{\mathrm{2}} } \\ $$$${B}={P}_{\mathrm{2}} {U}+{P}_{\mathrm{1}} \left(\mathrm{4}\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }\right)^{−\frac{\mathrm{4}}{\mathrm{3}}} −{P}_{\mathrm{2}} \left(\mathrm{4}\frac{{P}_{\mathrm{1}} }{{P}_{\mathrm{2}} }\right)^{−\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${B}={P}_{\mathrm{2}} {U}+{P}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{3}}} {P}_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{4}^{−\frac{\mathrm{4}}{\mathrm{3}}} −{P}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{3}}} {P}_{\mathrm{2}} ^{\frac{\mathrm{2}}{\mathrm{3}}} \mathrm{4}^{−\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${B}={P}_{\mathrm{2}} {U}+{P}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{3}}} {P}_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{4}^{−\frac{\mathrm{4}}{\mathrm{3}}} −\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{3}}} \right) \\ $$$${B}={P}_{\mathrm{2}} {U}+{P}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{3}}} {P}_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{3}}} =\left(\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${B}={P}_{\mathrm{2}} {U}−\frac{\mathrm{3}}{\mathrm{8}}{P}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{3}}} {P}_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${B}={P}_{\mathrm{2}} {U}−\frac{\mathrm{3}}{\mathrm{8}}\left({P}_{\mathrm{1}} {P}_{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\begin{array}{|c|}{{B}=\mathrm{2}{P}_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {P}_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {U}^{\frac{\mathrm{1}}{\mathrm{2}}} }\\\hline\end{array} \\ $$

Commented by nECxx2 last updated on 21/Mar/25

Thank you so much

$${Thank}\:{you}\:{so}\:{much} \\ $$

Commented by nECxx2 last updated on 21/Mar/25

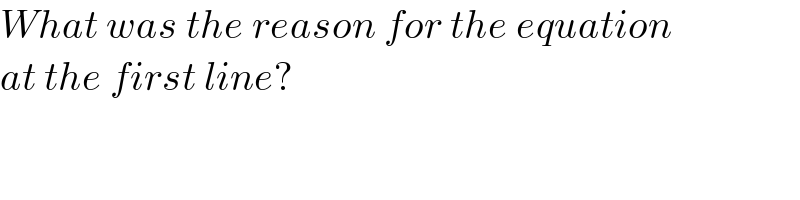
What was the reason for the equation at the first line?

$${What}\:{was}\:{the}\:{reason}\:{for}\:{the}\:{equation} \\ $$$${at}\:{the}\:{first}\:{line}? \\ $$

Commented by nECxx2 last updated on 21/Mar/25

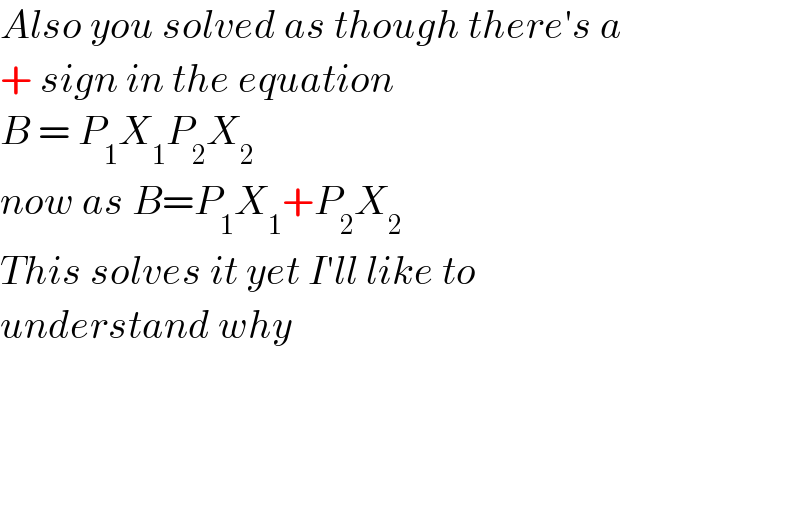
Also you solved as though there′s a + sign in the equation B = P_1 X_1 P_2 X_2 now as B=P_1 X_1 +P_2 X_2 This solves it yet I′ll like to understand why

$${Also}\:{you}\:{solved}\:{as}\:{though}\:{there}'{s}\:{a} \\ $$$$+\:{sign}\:{in}\:{the}\:{equation} \\ $$$${B}\:=\:{P}_{\mathrm{1}} {X}_{\mathrm{1}} {P}_{\mathrm{2}} {X}_{\mathrm{2}} \\ $$$${now}\:{as}\:{B}={P}_{\mathrm{1}} {X}_{\mathrm{1}} +{P}_{\mathrm{2}} {X}_{\mathrm{2}} \\ $$$${This}\:{solves}\:{it}\:{yet}\:{I}'{ll}\:{like}\:{to} \\ $$$${understand}\:{why} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by nECxx2 last updated on 21/Mar/25

After going through it again I have even more questions. Hiw come line 13? Please, I only need clarity as I am a learner. Thank you.

$${After}\:{going}\:{through}\:{it}\:{again}\:{I}\:{have} \\ $$$${even}\:{more}\:{questions}.\:{Hiw}\:{come} \\ $$$${line}\:\mathrm{13}? \\ $$$${Please},\:{I}\:{only}\:{need}\:{clarity}\:{as}\:{I}\:{am} \\ $$$${a}\:{learner}.\:{Thank}\:{you}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com