
Question Number 22154 by Joel577 last updated on 12/Oct/17
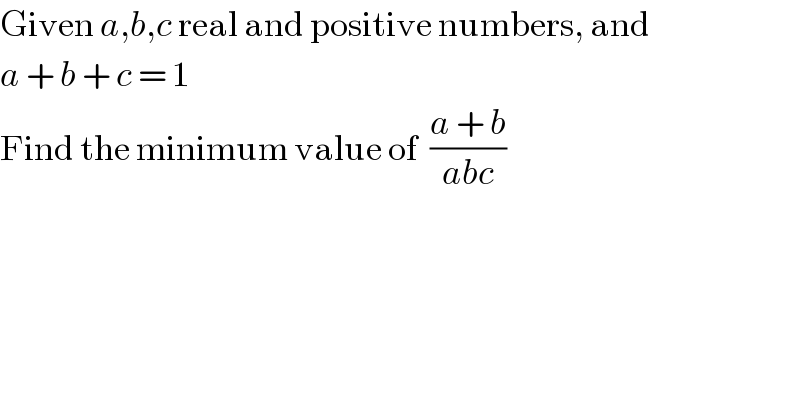
$$\mathrm{Given}\:{a},{b},{c}\:\mathrm{real}\:\mathrm{and}\:\mathrm{positive}\:\mathrm{numbers},\:\mathrm{and} \\ $$$${a}\:+\:{b}\:+\:{c}\:=\:\mathrm{1} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\:\frac{{a}\:+\:{b}}{{abc}} \\ $$
Answered by ajfour last updated on 12/Oct/17
![let a=cx and b=cy then c(x+y+1)=1 z=((a+b)/(abc)) =((x+y)/(c^2 xy)) =(((x+y)(x+y+1)^2 )/(xy)) As z is minimum, (∂z/∂x) =((x[(x+y+1)^2 +2(x+y)(x+y+1)]−(x+y)(x+y+1)^2 )/(x^2 y)) =0 ⇒ x[x+y+1+2x+2y]−(x+y)(x+y+1)=0 3x^2 +3xy+x−x^2 −y^2 −2xy−x−y=0 2x^2 +xy−y^2 −y=0 2x^2 +(x−1)y−y^2 =0 ...(i) similarly (∂z/∂y)=0 shall give 2y^2 +(y−1)x−x^2 =0 ...(ii) ⇒ x=y so 2x^2 +x^2 −x−x^2 =0 ⇒ 2x^2 −x=0 or x(x−(1/2))=0 we shall choose x=y=(1/2) since a, b, and c are +ve real numbers. Then a=(c/2) ; b=(c/2) ⇒ (c/2)+(c/2)+c =1 so c=(1/2) , a=(1/4) , b=(1/4) ⇒ min( ((a+b)/(abc)) )= ((1/2)/(1/32)) =16 .](Q22155.png)
$${let}\:{a}={cx}\:\:\:\:{and}\:\:{b}={cy} \\ $$$${then}\:\:\:{c}\left({x}+{y}+\mathrm{1}\right)=\mathrm{1} \\ $$$${z}=\frac{{a}+{b}}{{abc}}\:=\frac{{x}+{y}}{{c}^{\mathrm{2}} {xy}}\:=\frac{\left({x}+{y}\right)\left({x}+{y}+\mathrm{1}\right)^{\mathrm{2}} }{{xy}} \\ $$$${As}\:{z}\:{is}\:{minimum}, \\ $$$$\frac{\partial{z}}{\partial{x}}\:=\frac{{x}\left[\left({x}+{y}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+{y}\right)\left({x}+{y}+\mathrm{1}\right)\right]−\left({x}+{y}\right)\left({x}+{y}+\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} {y}}\:=\mathrm{0} \\ $$$$\Rightarrow\:{x}\left[{x}+{y}+\mathrm{1}+\mathrm{2}{x}+\mathrm{2}{y}\right]−\left({x}+{y}\right)\left({x}+{y}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{xy}+{x}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} −\mathrm{2}{xy}−{x}−{y}=\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +{xy}−{y}^{\mathrm{2}} −{y}=\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\left({x}−\mathrm{1}\right){y}−{y}^{\mathrm{2}} =\mathrm{0}\:\:\:\:\:\:\:...\left({i}\right) \\ $$$${similarly}\:\:\frac{\partial{z}}{\partial{y}}=\mathrm{0}\:\:{shall}\:{give} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} +\left({y}−\mathrm{1}\right){x}−{x}^{\mathrm{2}} =\mathrm{0}\:\:\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow\:\:\:{x}={y} \\ $$$${so}\:\:\:\mathrm{2}{x}^{\mathrm{2}} +{x}^{\mathrm{2}} −{x}−{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\:\:\mathrm{2}{x}^{\mathrm{2}} −{x}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{or}\:\:\:\:\:{x}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\:\:{we}\:{shall}\:{choose}\:{x}={y}=\frac{\mathrm{1}}{\mathrm{2}}\:{since} \\ $$$${a},\:{b},\:{and}\:{c}\:{are}\:+{ve}\:{real}\:{numbers}. \\ $$$${Then}\:\:\:\:{a}=\frac{{c}}{\mathrm{2}}\:\:\:\:;\:\:\:\:{b}=\frac{{c}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\Rightarrow\:\:\:\frac{{c}}{\mathrm{2}}+\frac{{c}}{\mathrm{2}}+{c}\:=\mathrm{1}\:\:\: \\ $$$${so}\:\:\:\:\:{c}=\frac{\mathrm{1}}{\mathrm{2}}\:,\:\:{a}=\frac{\mathrm{1}}{\mathrm{4}}\:,\:\:\:{b}=\frac{\mathrm{1}}{\mathrm{4}}\: \\ $$$$\Rightarrow\:\:{min}\left(\:\frac{{a}+{b}}{{abc}}\:\right)=\:\frac{\mathrm{1}/\mathrm{2}}{\mathrm{1}/\mathrm{32}}\:=\mathrm{16}\:. \\ $$
Commented by Joel577 last updated on 12/Oct/17
$${Thank}\:{you}\:{very}\:{much}\:{Sir} \\ $$
Commented by Joel577 last updated on 12/Oct/17
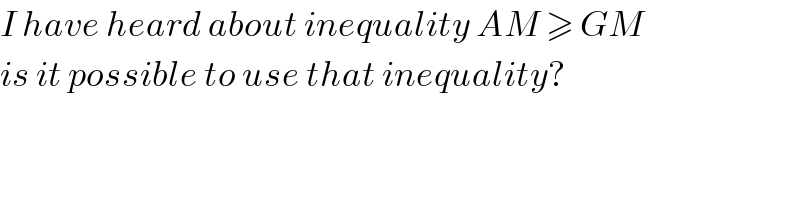
$${I}\:{have}\:{heard}\:{about}\:{inequality}\:{AM}\:\geqslant\:{GM} \\ $$$${is}\:{it}\:{possible}\:{to}\:{use}\:{that}\:{inequality}? \\ $$
Answered by ajfour last updated on 12/Oct/17
![let a+b=p and f=((a+b)/(abc)) =(p/(abc)) = ((4p)/((4ab)c)) ⇒ f =((4p)/([(a+b)^2 −(a−b)^2 ]c)) or f=((4p)/([p^2 −(a−b)^2 ]c)) For f to be minimum , a=b ⇒ f=((4p)/(p^2 c)) = (4/(pc)) but a+b+c =1 ⇒ p+c=1 max. of cp results when c=p ⇒ c=(1/2) and p=(1/2) So f =(4/(cp)) =(4/((1/4))) =16 .](Q22171.png)
$${let}\:\:{a}+{b}={p} \\ $$$${and}\:\:\:{f}=\frac{{a}+{b}}{{abc}}\:=\frac{{p}}{{abc}}\:\:\:=\:\frac{\mathrm{4}{p}}{\left(\mathrm{4}{ab}\right){c}} \\ $$$$\:\Rightarrow\:\:\:\:\:\:{f}\:=\frac{\mathrm{4}{p}}{\left[\left({a}+{b}\right)^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} \right]{c}} \\ $$$$\:\:\:\:\:{or}\:\:{f}=\frac{\mathrm{4}{p}}{\left[{p}^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} \right]{c}} \\ $$$${For}\:{f}\:{to}\:{be}\:{minimum}\:,\:\:\:{a}={b} \\ $$$$\Rightarrow\:\:\:\:\:{f}=\frac{\mathrm{4}{p}}{{p}^{\mathrm{2}} {c}}\:=\:\frac{\mathrm{4}}{{pc}} \\ $$$$\:\:\:\:\:{but}\:{a}+{b}+{c}\:=\mathrm{1}\:\:\Rightarrow\:\:\:{p}+{c}=\mathrm{1} \\ $$$${max}.\:{of}\:{cp}\:{results}\:{when}\:{c}={p} \\ $$$$\Rightarrow\:\:\:\:\:{c}=\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{p}=\frac{\mathrm{1}}{\mathrm{2}}\:\: \\ $$$$\:\:\:\:\:{So}\:\:\boldsymbol{{f}}\:=\frac{\mathrm{4}}{\boldsymbol{{cp}}}\:=\frac{\mathrm{4}}{\left(\mathrm{1}/\mathrm{4}\right)}\:=\mathrm{16}\:. \\ $$
Commented by Joel577 last updated on 13/Oct/17
$${thank}\:{you}\:{very}\:{much} \\ $$
