
Question Number 213663 by efronzo1 last updated on 13/Nov/24
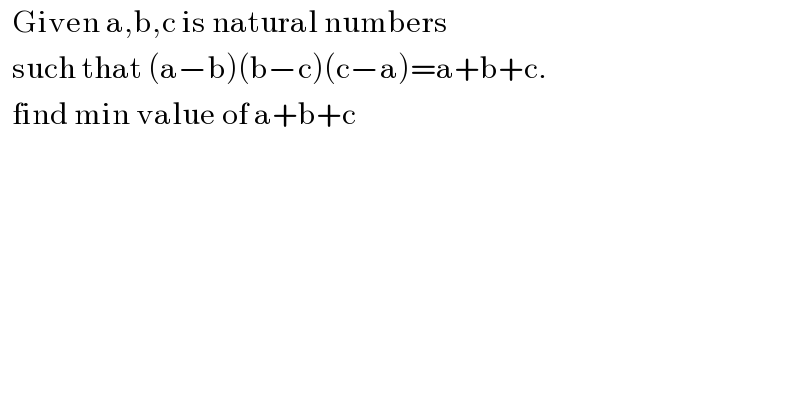
$$\:\:\mathrm{Given}\:\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{is}\:\mathrm{natural}\:\mathrm{numbers} \\ $$$$\:\:\mathrm{such}\:\mathrm{that}\:\left(\mathrm{a}−\mathrm{b}\right)\left(\mathrm{b}−\mathrm{c}\right)\left(\mathrm{c}−\mathrm{a}\right)=\mathrm{a}+\mathrm{b}+\mathrm{c}. \\ $$$$\:\:\mathrm{find}\:\mathrm{min}\:\mathrm{value}\:\mathrm{of}\:\mathrm{a}+\mathrm{b}+\mathrm{c}\: \\ $$
Answered by Ghisom last updated on 13/Nov/24
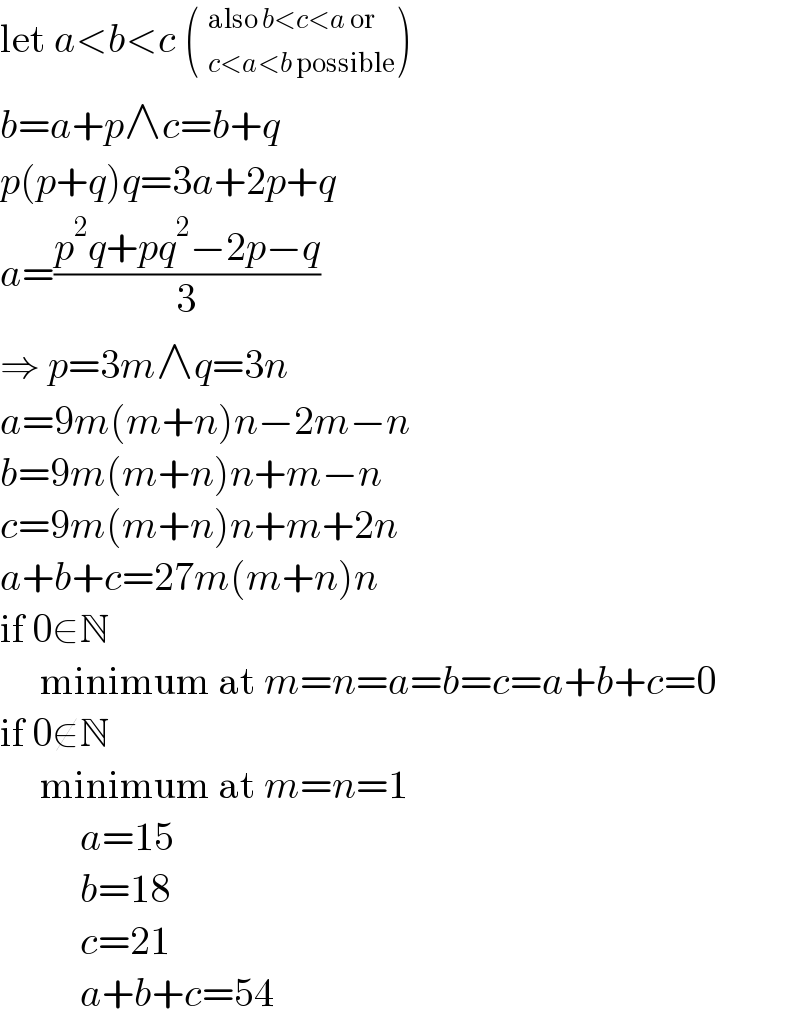
$$\mathrm{let}\:{a}<{b}<{c}\:\left(\:_{{c}<{a}<{b}\:\mathrm{possible}} ^{\mathrm{also}\:{b}<{c}<{a}\:\mathrm{or}} \right) \\ $$$${b}={a}+{p}\wedge{c}={b}+{q} \\ $$$${p}\left({p}+{q}\right){q}=\mathrm{3}{a}+\mathrm{2}{p}+{q} \\ $$$${a}=\frac{{p}^{\mathrm{2}} {q}+{pq}^{\mathrm{2}} −\mathrm{2}{p}−{q}}{\mathrm{3}} \\ $$$$\Rightarrow\:{p}=\mathrm{3}{m}\wedge{q}=\mathrm{3}{n} \\ $$$${a}=\mathrm{9}{m}\left({m}+{n}\right){n}−\mathrm{2}{m}−{n} \\ $$$${b}=\mathrm{9}{m}\left({m}+{n}\right){n}+{m}−{n} \\ $$$${c}=\mathrm{9}{m}\left({m}+{n}\right){n}+{m}+\mathrm{2}{n} \\ $$$${a}+{b}+{c}=\mathrm{27}{m}\left({m}+{n}\right){n} \\ $$$$\mathrm{if}\:\mathrm{0}\in\mathbb{N} \\ $$$$\:\:\:\:\:\mathrm{minimum}\:\mathrm{at}\:{m}={n}={a}={b}={c}={a}+{b}+{c}=\mathrm{0} \\ $$$$\mathrm{if}\:\mathrm{0}\notin\mathbb{N} \\ $$$$\:\:\:\:\:\mathrm{minimum}\:\mathrm{at}\:{m}={n}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}=\mathrm{15} \\ $$$$\:\:\:\:\:\:\:\:\:\:{b}=\mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:\:\:{c}=\mathrm{21} \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}+{b}+{c}=\mathrm{54} \\ $$
