
Question Number 26917 by Joel578 last updated on 31/Dec/17
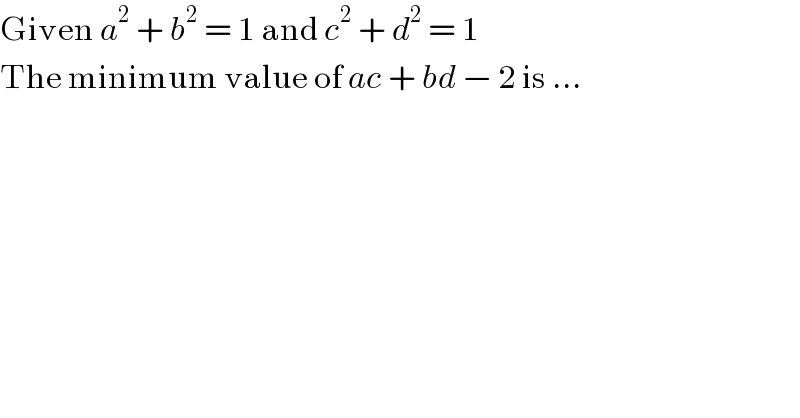
$$\mathrm{Given}\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:=\:\mathrm{1}\:\mathrm{and}\:{c}^{\mathrm{2}} \:+\:{d}^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$$\mathrm{The}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:{ac}\:+\:{bd}\:−\:\mathrm{2}\:\mathrm{is}\:... \\ $$
Commented by prakash jain last updated on 31/Dec/17
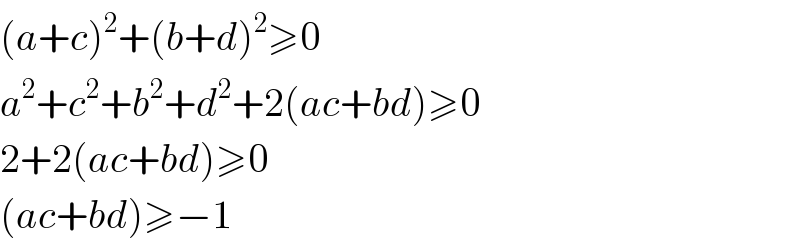
$$\left({a}+{c}\right)^{\mathrm{2}} +\left({b}+{d}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$${a}^{\mathrm{2}} +{c}^{\mathrm{2}} +{b}^{\mathrm{2}} +{d}^{\mathrm{2}} +\mathrm{2}\left({ac}+{bd}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{2}+\mathrm{2}\left({ac}+{bd}\right)\geqslant\mathrm{0} \\ $$$$\left({ac}+{bd}\right)\geqslant−\mathrm{1} \\ $$
Commented by Joel578 last updated on 31/Dec/17
$${thank}\:{you}\:{very}\:{much} \\ $$
Answered by ajfour last updated on 31/Dec/17
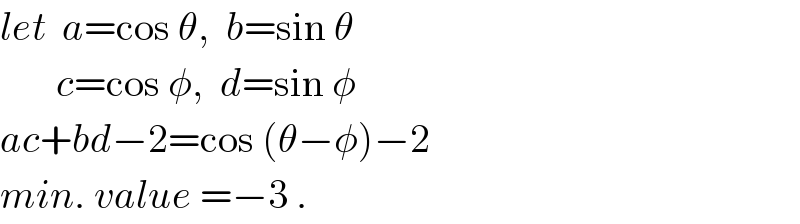
$${let}\:\:{a}=\mathrm{cos}\:\theta,\:\:{b}=\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:{c}=\mathrm{cos}\:\phi,\:\:{d}=\mathrm{sin}\:\phi \\ $$$${ac}+{bd}−\mathrm{2}=\mathrm{cos}\:\left(\theta−\phi\right)−\mathrm{2} \\ $$$${min}.\:{value}\:=−\mathrm{3}\:. \\ $$
Commented by Joel578 last updated on 02/Jan/18
$${thank}\:{you}\:{very}\:{much} \\ $$
