
Question Number 114638 by bobhans last updated on 20/Sep/20
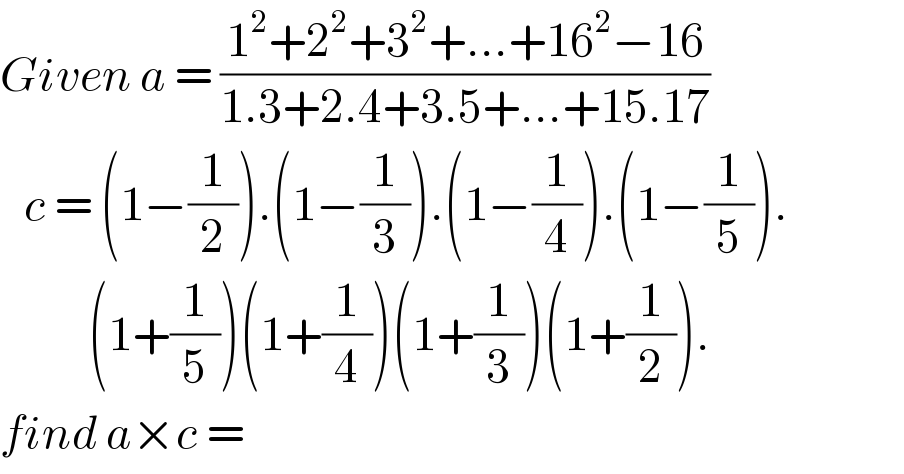
$${Given}\:{a}\:=\:\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +...+\mathrm{16}^{\mathrm{2}} −\mathrm{16}}{\mathrm{1}.\mathrm{3}+\mathrm{2}.\mathrm{4}+\mathrm{3}.\mathrm{5}+...+\mathrm{15}.\mathrm{17}} \\ $$$$\:\:\:{c}\:=\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right).\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right).\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right).\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}\right). \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right). \\ $$$${find}\:{a}×{c}\:=\: \\ $$
Answered by bemath last updated on 20/Sep/20
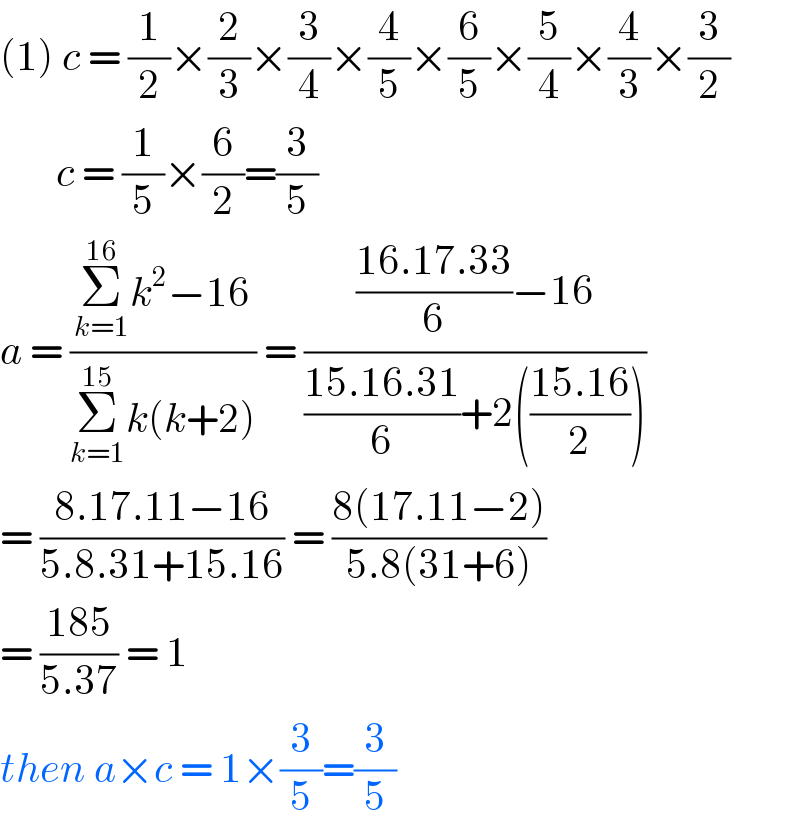
$$\left(\mathrm{1}\right)\:{c}\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{4}}{\mathrm{5}}×\frac{\mathrm{6}}{\mathrm{5}}×\frac{\mathrm{5}}{\mathrm{4}}×\frac{\mathrm{4}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:{c}\:=\:\frac{\mathrm{1}}{\mathrm{5}}×\frac{\mathrm{6}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$${a}\:=\:\frac{\underset{{k}=\mathrm{1}} {\overset{\mathrm{16}} {\sum}}{k}^{\mathrm{2}} −\mathrm{16}}{\underset{{k}=\mathrm{1}} {\overset{\mathrm{15}} {\sum}}{k}\left({k}+\mathrm{2}\right)}\:=\:\frac{\frac{\mathrm{16}.\mathrm{17}.\mathrm{33}}{\mathrm{6}}−\mathrm{16}}{\frac{\mathrm{15}.\mathrm{16}.\mathrm{31}}{\mathrm{6}}+\mathrm{2}\left(\frac{\mathrm{15}.\mathrm{16}}{\mathrm{2}}\right)} \\ $$$$=\:\frac{\mathrm{8}.\mathrm{17}.\mathrm{11}−\mathrm{16}}{\mathrm{5}.\mathrm{8}.\mathrm{31}+\mathrm{15}.\mathrm{16}}\:=\:\frac{\mathrm{8}\left(\mathrm{17}.\mathrm{11}−\mathrm{2}\right)}{\mathrm{5}.\mathrm{8}\left(\mathrm{31}+\mathrm{6}\right)} \\ $$$$=\:\frac{\mathrm{185}}{\mathrm{5}.\mathrm{37}}\:=\:\mathrm{1} \\ $$$${then}\:{a}×{c}\:=\:\mathrm{1}×\frac{\mathrm{3}}{\mathrm{5}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$
Commented by PRITHWISH SEN 2 last updated on 20/Sep/20

$$\mathrm{c}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$
