Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 161130 by blackmamba last updated on 12/Dec/21

Given P(x) is polynomial such that P(3x)= P ′(x).P ′′(x) . Find the tangent of curve y = P(x) parallel to the line y= 4x−2.

$$\:{Given}\:{P}\left({x}\right)\:{is}\:{polynomial}\:{such}\:{that} \\ $$$$\:{P}\left(\mathrm{3}{x}\right)=\:{P}\:'\left({x}\right).{P}\:''\left({x}\right)\:.\:{Find}\:{the}\:{tangent} \\ $$$$\:{of}\:{curve}\:{y}\:=\:{P}\left({x}\right)\:{parallel}\:{to}\:{the}\:{line} \\ $$$$\:{y}=\:\mathrm{4}{x}−\mathrm{2}.\: \\ $$

Answered by FongXD last updated on 12/Dec/21

Given: P(3x)=P′(x)∙P′′(x) Degree of L.H.S=n Degree of R.H.S=(n−1)+(n−2)=2n−3 L.H.S=R.H.S, ⇔ n=2n−3, ⇒ n=3 therefore, P(x)=ax^3 +bx^2 +cx+d then P(3x)=27ax^3 +9bx^2 +3cx+d • P′(x)=3ax^2 +2bx+c • P′′(x)=6ax+2b ⇒ P′(x)∙P′′(x)=18a^2 x^3 +18abx^2 +(4b^2 +6ac)x+2bc P(3x)=P′(x)∙P′′(x) then { ((27a=18a^2 )),((9b^2 =18ab)),((3c=4b^2 +6ac)),((d=2bc)) :}, ⇒ { ((a=(3/2))),((b=3)),((3c=36+9c, ⇒ c=−6)),((d=−36)) :} then P(x)=(3/2)x^3 +3x^2 −6x−36 and P′(x)=(9/2)x^2 +6x−6 Given that tangent line is parallel to the line y=4x−2 ⇒ P′(x_0 )=4, ⇔ (9/2)x_0 ^2 +6x_0 −6=4 ⇔ 9x_0 ^2 +12x_0 −20=0 ⇒ x_0 =((−6±(√(36+180)))/9)=((−2±2(√6))/3) ⇒ P(x_0 )=(3/2)(((−2±2(√6))/3))^3 +3(((−2±2(√6))/3))^2 −6(((−2±2(√6))/3))−36 ⇒ { ((P(x_0 )=((−280−24(√6))/9), if x_0 =((−2+2(√6))/3))),((P(x_0 )=((−280+24(√6))/9), if x_0 =((−2−2(√6))/3))) :} Tangent line: y=P′(x_0 )(x−x_0 )+P(x_0 ) ⇒ { ((y=4(x−((−2+2(√6))/3))+((−280−24(√6))/9))),((y=4(x−((−2−2(√6))/3))+((−280+24(√6))/9))) :} ⇒ { ((y=4x−((256+48(√6))/9))),((y=4x−((256−48(√6))/9))) :}

$$\mathrm{Given}:\:\mathrm{P}\left(\mathrm{3x}\right)=\mathrm{P}'\left(\mathrm{x}\right)\centerdot\mathrm{P}''\left(\mathrm{x}\right) \\ $$$$\mathrm{Degree}\:\mathrm{of}\:\mathrm{L}.\mathrm{H}.\mathrm{S}=\mathrm{n} \\ $$$$\mathrm{Degree}\:\mathrm{of}\:\mathrm{R}.\mathrm{H}.\mathrm{S}=\left(\mathrm{n}−\mathrm{1}\right)+\left(\mathrm{n}−\mathrm{2}\right)=\mathrm{2n}−\mathrm{3} \\ $$$$\mathrm{L}.\mathrm{H}.\mathrm{S}=\mathrm{R}.\mathrm{H}.\mathrm{S},\:\Leftrightarrow\:\mathrm{n}=\mathrm{2n}−\mathrm{3},\:\Rightarrow\:\mathrm{n}=\mathrm{3} \\ $$$$\mathrm{therefore},\:\mathrm{P}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{3}} +\mathrm{bx}^{\mathrm{2}} +\mathrm{cx}+\mathrm{d} \\ $$$$\mathrm{then}\:\mathrm{P}\left(\mathrm{3x}\right)=\mathrm{27ax}^{\mathrm{3}} +\mathrm{9bx}^{\mathrm{2}} +\mathrm{3cx}+\mathrm{d} \\ $$$$\bullet\:\mathrm{P}'\left(\mathrm{x}\right)=\mathrm{3ax}^{\mathrm{2}} +\mathrm{2bx}+\mathrm{c} \\ $$$$\bullet\:\mathrm{P}''\left(\mathrm{x}\right)=\mathrm{6ax}+\mathrm{2b} \\ $$$$\Rightarrow\:\mathrm{P}'\left(\mathrm{x}\right)\centerdot\mathrm{P}''\left(\mathrm{x}\right)=\mathrm{18a}^{\mathrm{2}} \mathrm{x}^{\mathrm{3}} +\mathrm{18abx}^{\mathrm{2}} +\left(\mathrm{4b}^{\mathrm{2}} +\mathrm{6ac}\right)\mathrm{x}+\mathrm{2bc} \\ $$$$\:\:\:\:\:\mathrm{P}\left(\mathrm{3x}\right)=\mathrm{P}'\left(\mathrm{x}\right)\centerdot\mathrm{P}''\left(\mathrm{x}\right) \\ $$$$\mathrm{then}\:\begin{cases}{\mathrm{27a}=\mathrm{18a}^{\mathrm{2}} }\\{\mathrm{9b}^{\mathrm{2}} =\mathrm{18ab}}\\{\mathrm{3c}=\mathrm{4b}^{\mathrm{2}} +\mathrm{6ac}}\\{\mathrm{d}=\mathrm{2bc}}\end{cases},\:\Rightarrow\:\begin{cases}{\mathrm{a}=\frac{\mathrm{3}}{\mathrm{2}}}\\{\mathrm{b}=\mathrm{3}}\\{\mathrm{3c}=\mathrm{36}+\mathrm{9c},\:\Rightarrow\:\mathrm{c}=−\mathrm{6}}\\{\mathrm{d}=−\mathrm{36}}\end{cases} \\ $$$$\mathrm{then}\:\mathrm{P}\left(\mathrm{x}\right)=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} −\mathrm{6x}−\mathrm{36} \\ $$$$\mathrm{and}\:\mathrm{P}'\left(\mathrm{x}\right)=\frac{\mathrm{9}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\mathrm{6x}−\mathrm{6} \\ $$$$\mathrm{Given}\:\mathrm{that}\:\mathrm{tangent}\:\mathrm{line}\:\mathrm{is}\:\mathrm{parallel}\:\mathrm{to}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{4x}−\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{P}'\left(\mathrm{x}_{\mathrm{0}} \right)=\mathrm{4},\:\Leftrightarrow\:\frac{\mathrm{9}}{\mathrm{2}}\mathrm{x}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{6x}_{\mathrm{0}} −\mathrm{6}=\mathrm{4} \\ $$$$\Leftrightarrow\:\mathrm{9x}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{12x}_{\mathrm{0}} −\mathrm{20}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}_{\mathrm{0}} =\frac{−\mathrm{6}\pm\sqrt{\mathrm{36}+\mathrm{180}}}{\mathrm{9}}=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{P}\left(\mathrm{x}_{\mathrm{0}} \right)=\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\right)^{\mathrm{3}} +\mathrm{3}\left(\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{6}\left(\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\right)−\mathrm{36} \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{P}\left(\mathrm{x}_{\mathrm{0}} \right)=\frac{−\mathrm{280}−\mathrm{24}\sqrt{\mathrm{6}}}{\mathrm{9}},\:\mathrm{if}\:\mathrm{x}_{\mathrm{0}} =\frac{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}}\\{\mathrm{P}\left(\mathrm{x}_{\mathrm{0}} \right)=\frac{−\mathrm{280}+\mathrm{24}\sqrt{\mathrm{6}}}{\mathrm{9}},\:\mathrm{if}\:\mathrm{x}_{\mathrm{0}} =\frac{−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}}\end{cases} \\ $$$$\mathrm{Tangent}\:\mathrm{line}:\:\mathrm{y}=\mathrm{P}'\left(\mathrm{x}_{\mathrm{0}} \right)\left(\mathrm{x}−\mathrm{x}_{\mathrm{0}} \right)+\mathrm{P}\left(\mathrm{x}_{\mathrm{0}} \right) \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{y}=\mathrm{4}\left(\mathrm{x}−\frac{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\right)+\frac{−\mathrm{280}−\mathrm{24}\sqrt{\mathrm{6}}}{\mathrm{9}}}\\{\mathrm{y}=\mathrm{4}\left(\mathrm{x}−\frac{−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\right)+\frac{−\mathrm{280}+\mathrm{24}\sqrt{\mathrm{6}}}{\mathrm{9}}}\end{cases} \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{y}=\mathrm{4x}−\frac{\mathrm{256}+\mathrm{48}\sqrt{\mathrm{6}}}{\mathrm{9}}}\\{\mathrm{y}=\mathrm{4x}−\frac{\mathrm{256}−\mathrm{48}\sqrt{\mathrm{6}}}{\mathrm{9}}}\end{cases} \\ $$

Commented by cortano last updated on 12/Dec/21

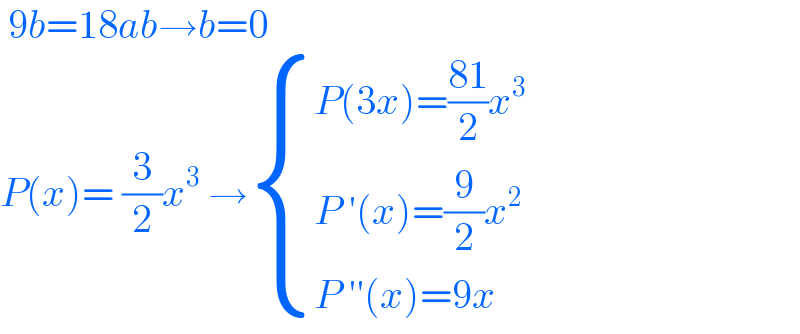
9b=18ab→b=0 P(x)= (3/2)x^3 → { ((P(3x)=((81)/2)x^3 )),((P ′(x)=(9/2)x^2 )),((P ′′(x)=9x)) :}

$$\:\mathrm{9}{b}=\mathrm{18}{ab}\rightarrow{b}=\mathrm{0} \\ $$$${P}\left({x}\right)=\:\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{3}} \:\rightarrow\begin{cases}{{P}\left(\mathrm{3}{x}\right)=\frac{\mathrm{81}}{\mathrm{2}}{x}^{\mathrm{3}} }\\{{P}\:'\left({x}\right)=\frac{\mathrm{9}}{\mathrm{2}}{x}^{\mathrm{2}} }\\{{P}\:''\left({x}\right)=\mathrm{9}{x}}\end{cases} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com