
Previous in Relation and Functions Next in Relation and Functions
Question Number 92197 by jagoll last updated on 05/May/20
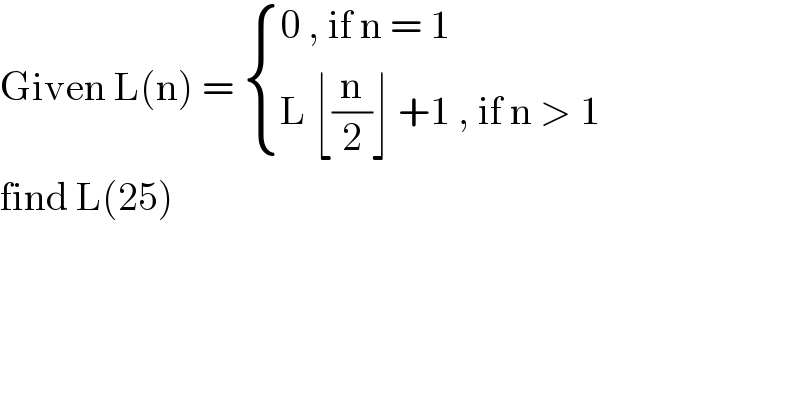
$$\mathrm{Given}\:\mathrm{L}\left(\mathrm{n}\right)\:=\:\begin{cases}{\mathrm{0}\:,\:\mathrm{if}\:\mathrm{n}\:=\:\mathrm{1}}\\{\mathrm{L}\:\lfloor\frac{\mathrm{n}}{\mathrm{2}}\rfloor\:+\mathrm{1}\:,\:\mathrm{if}\:\mathrm{n}\:>\:\mathrm{1}}\end{cases} \\ $$$$\mathrm{find}\:\mathrm{L}\left(\mathrm{25}\right)\: \\ $$
Commented by john santu last updated on 05/May/20
![L(25)= L(12)+1 = [ L(6) + 1 ] +1 = L(6) +2 = [ L(3)+1 ] +2 = L(3) +3 = [ L(1)+1 ] +3 = L(1) +4 = 0 + 4 = 4](Q92198.png)
$$\mathrm{L}\left(\mathrm{25}\right)=\:\mathrm{L}\left(\mathrm{12}\right)+\mathrm{1} \\ $$$$=\:\left[\:\mathrm{L}\left(\mathrm{6}\right)\:+\:\mathrm{1}\:\right]\:+\mathrm{1}\:=\:\mathrm{L}\left(\mathrm{6}\right)\:+\mathrm{2} \\ $$$$=\:\left[\:\mathrm{L}\left(\mathrm{3}\right)+\mathrm{1}\:\right]\:+\mathrm{2}\:=\:\mathrm{L}\left(\mathrm{3}\right)\:+\mathrm{3}\: \\ $$$$=\:\left[\:\mathrm{L}\left(\mathrm{1}\right)+\mathrm{1}\:\right]\:+\mathrm{3}\:=\:\mathrm{L}\left(\mathrm{1}\right)\:+\mathrm{4}\: \\ $$$$=\:\mathrm{0}\:+\:\mathrm{4}\:=\:\mathrm{4}\: \\ $$
