
Question Number 155496 by mathocean1 last updated on 01/Oct/21
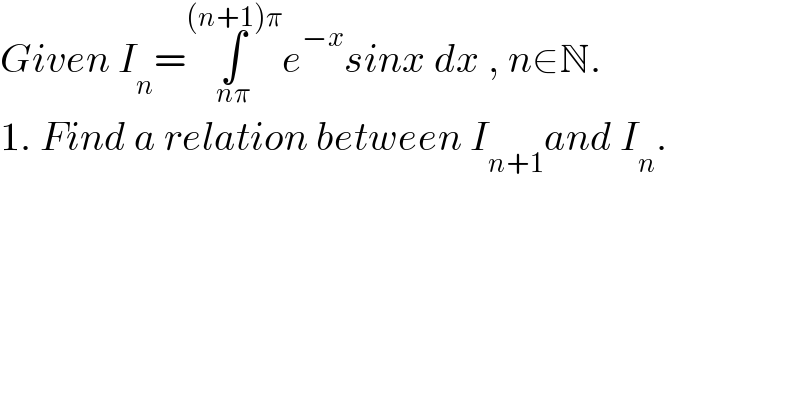
$${Given}\:{I}_{{n}} =\underset{{n}\pi} {\overset{\left({n}+\mathrm{1}\right)\pi} {\int}}{e}^{−{x}} {sinx}\:{dx}\:,\:{n}\in\mathbb{N}. \\ $$$$\mathrm{1}.\:{Find}\:{a}\:{relation}\:{between}\:{I}_{{n}+\mathrm{1}} {and}\:{I}_{{n}} . \\ $$
Answered by ArielVyny last updated on 01/Oct/21
![I_n =∫_(nπ) ^((n+1)π) e^(−x) sinxdx du=e^(−x) →u=−e^(−x) v=sinx→dv=cosx I_n =[−e^(−x) sinx]_(nπ) ^((n+1)π) +∫_(nπ) ^((n+1)) e^(−x) cosxdx du=e^(−x) →u=−e^(−x) v=cosx→dv=−sinx 2I_n =−[e^(−x) sinx+e^(−x) cosx]_(nπ) ^((n+1)π) 2I_n =−[e^(−π(n+1)) sin((n+1)π)+e^(−π(n+1)) cos((n+1)π)−e^(−nπ) sin(nπ)−e^(−nπ) cos(nπ)] 2I_n =−[e^(−π(n+1)) (sin(nπ)cosπ+cos(nπ)sinπ)+e^(−π(n+1)) (cosnπcosπ+sin(nπ)sin(π)−e^(−nπ) sin(nπ)−e^(−nπ) cos(nπ)] 2I_n =−[−e^(−π(n+1)) (−1)^n −e^(−nπ) (−1)^n ] 2I_n =(−1)^n e^(−π(n+1)) +(−1)^n e^(−nπ) 2I_(n+1) =(−1)^(n+1) e^(−π(n+2)) +(−1)^n e^(−(n+1)π) 2I_(n+1) −2I_n =(−1)^(n+1) e^(−π(n+2)) +(−1)^(n+1) e^(−nπ) I_(n+1) −I_n =(((−1)^(n+1) e^(−π(n+2)) +(−1)^(n+1) e^(−nπ) )/2)](Q155534.png)
$${I}_{{n}} =\int_{{n}\pi} ^{\left({n}+\mathrm{1}\right)\pi} {e}^{−{x}} {sinxdx} \\ $$$${du}={e}^{−{x}} \rightarrow{u}=−{e}^{−{x}} \\ $$$${v}={sinx}\rightarrow{dv}={cosx} \\ $$$${I}_{{n}} =\left[−{e}^{−{x}} {sinx}\right]_{{n}\pi} ^{\left({n}+\mathrm{1}\right)\pi} +\int_{{n}\pi} ^{\left({n}+\mathrm{1}\right)} {e}^{−{x}} {cosxdx} \\ $$$${du}={e}^{−{x}} \rightarrow{u}=−{e}^{−{x}} \\ $$$${v}={cosx}\rightarrow{dv}=−{sinx} \\ $$$$\mathrm{2}{I}_{{n}} =−\left[{e}^{−{x}} {sinx}+{e}^{−{x}} {cosx}\right]_{{n}\pi} ^{\left({n}+\mathrm{1}\right)\pi} \\ $$$$\mathrm{2}{I}_{{n}} =−\left[{e}^{−\pi\left({n}+\mathrm{1}\right)} {sin}\left(\left({n}+\mathrm{1}\right)\pi\right)+{e}^{−\pi\left({n}+\mathrm{1}\right)} {cos}\left(\left({n}+\mathrm{1}\right)\pi\right)−{e}^{−{n}\pi} {sin}\left({n}\pi\right)−{e}^{−{n}\pi} {cos}\left({n}\pi\right)\right] \\ $$$$\mathrm{2}{I}_{{n}} =−\left[{e}^{−\pi\left({n}+\mathrm{1}\right)} \left({sin}\left({n}\pi\right){cos}\pi+{cos}\left({n}\pi\right){sin}\pi\right)+{e}^{−\pi\left({n}+\mathrm{1}\right)} \left({cosn}\pi{cos}\pi+{sin}\left({n}\pi\right){sin}\left(\pi\right)−{e}^{−{n}\pi} {sin}\left({n}\pi\right)−{e}^{−{n}\pi} {cos}\left({n}\pi\right)\right]\right. \\ $$$$\mathrm{2}{I}_{{n}} =−\left[−{e}^{−\pi\left({n}+\mathrm{1}\right)} \left(−\mathrm{1}\right)^{{n}} −{e}^{−{n}\pi} \left(−\mathrm{1}\right)^{{n}} \right] \\ $$$$\mathrm{2}{I}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {e}^{−\pi\left({n}+\mathrm{1}\right)} +\left(−\mathrm{1}\right)^{{n}} {e}^{−{n}\pi} \\ $$$$\mathrm{2}{I}_{{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{−\pi\left({n}+\mathrm{2}\right)} +\left(−\mathrm{1}\right)^{{n}} {e}^{−\left({n}+\mathrm{1}\right)\pi} \\ $$$$\mathrm{2}{I}_{{n}+\mathrm{1}} −\mathrm{2}{I}_{{n}} =\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{−\pi\left({n}+\mathrm{2}\right)} +\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{−{n}\pi} \\ $$$${I}_{{n}+\mathrm{1}} −{I}_{{n}} =\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{−\pi\left({n}+\mathrm{2}\right)} +\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{−{n}\pi} }{\mathrm{2}} \\ $$
Commented by mathocean1 last updated on 22/Oct/21

$${thank}\:{you}\: \\ $$
