
Question Number 159111 by mathocean1 last updated on 13/Nov/21
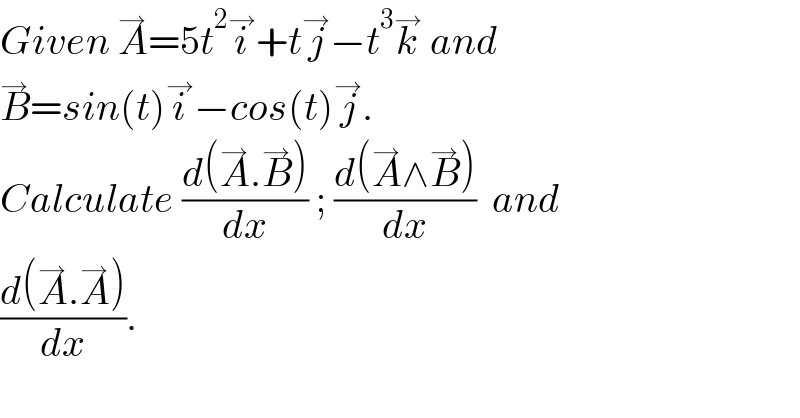
$${Given}\:\overset{\rightarrow} {{A}}=\mathrm{5}{t}^{\mathrm{2}} \overset{\rightarrow} {{i}}+{t}\overset{\rightarrow} {{j}}−{t}^{\mathrm{3}} \overset{\rightarrow} {{k}}\:{and} \\ $$$$\overset{\rightarrow} {{B}}={sin}\left({t}\right)\overset{\rightarrow} {{i}}−{cos}\left({t}\right)\overset{\rightarrow} {{j}}. \\ $$$${Calculate}\:\frac{{d}\left(\overset{\rightarrow} {{A}}.\overset{\rightarrow} {{B}}\right)}{{dx}}\:;\:\frac{{d}\left(\overset{\rightarrow} {{A}}\wedge\overset{\rightarrow} {{B}}\right)}{{dx}}\:\:{and} \\ $$$$\frac{{d}\left(\overset{\rightarrow} {{A}}.\overset{\rightarrow} {{A}}\right)}{{dx}}. \\ $$
Answered by physicstutes last updated on 13/Nov/21
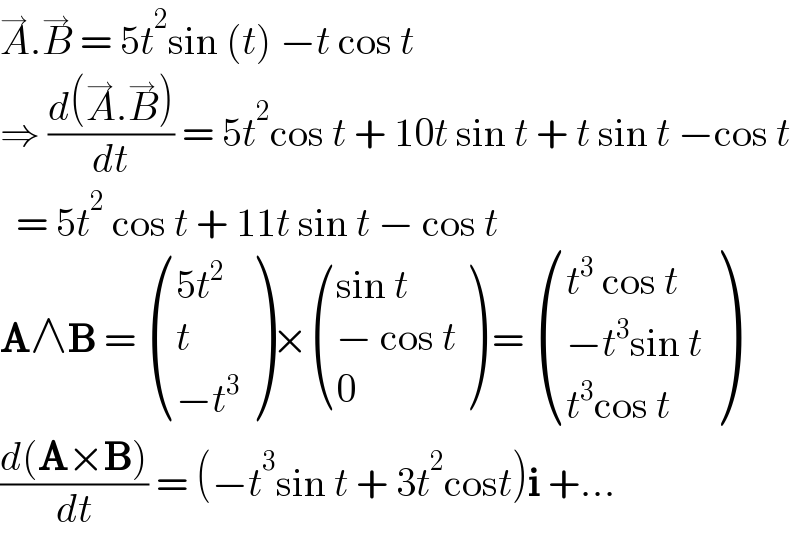
$$\overset{\rightarrow} {{A}}.\overset{\rightarrow} {{B}}\:=\:\mathrm{5}{t}^{\mathrm{2}} \mathrm{sin}\:\left({t}\right)\:−{t}\:\mathrm{cos}\:{t} \\ $$$$\Rightarrow\:\frac{{d}\left(\overset{\rightarrow} {{A}}.\overset{\rightarrow} {{B}}\right)}{{dt}}\:=\:\mathrm{5}{t}^{\mathrm{2}} \mathrm{cos}\:{t}\:+\:\mathrm{10}{t}\:\mathrm{sin}\:{t}\:+\:{t}\:\mathrm{sin}\:{t}\:−\mathrm{cos}\:{t} \\ $$$$\:\:=\:\mathrm{5}{t}^{\mathrm{2}} \:\mathrm{cos}\:{t}\:+\:\mathrm{11}{t}\:\mathrm{sin}\:{t}\:−\:\mathrm{cos}\:{t} \\ $$$$\boldsymbol{\mathrm{A}}\wedge\boldsymbol{\mathrm{B}}\:=\:\begin{pmatrix}{\mathrm{5}{t}^{\mathrm{2}} \:}\\{{t}}\\{−{t}^{\mathrm{3}} }\end{pmatrix}×\begin{pmatrix}{\mathrm{sin}\:{t}}\\{−\:\mathrm{cos}\:{t}}\\{\mathrm{0}}\end{pmatrix}\:=\:\begin{pmatrix}{{t}^{\mathrm{3}} \:\mathrm{cos}\:{t}}\\{−{t}^{\mathrm{3}} \mathrm{sin}\:{t}}\\{{t}^{\mathrm{3}} \mathrm{cos}\:{t}}\end{pmatrix} \\ $$$$\frac{{d}\left(\boldsymbol{\mathrm{A}}×\boldsymbol{\mathrm{B}}\right)}{{dt}}\:=\:\left(−{t}^{\mathrm{3}} \mathrm{sin}\:{t}\:+\:\mathrm{3}{t}^{\mathrm{2}} \mathrm{cos}{t}\right)\boldsymbol{\mathrm{i}}\:+... \\ $$
