Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 130047 by liberty last updated on 22/Jan/21

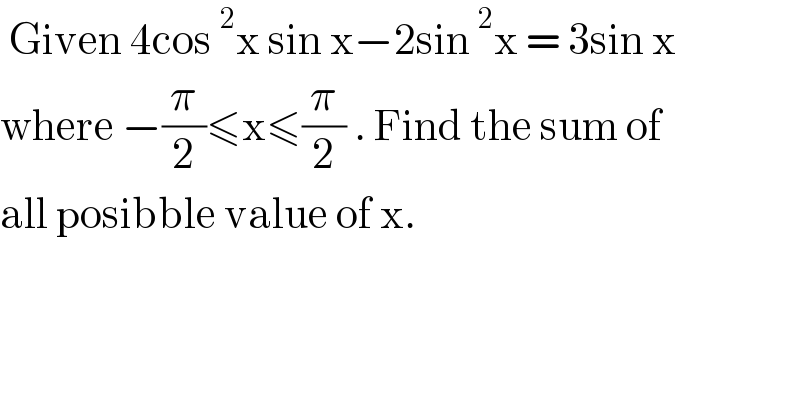
Given 4cos^2 x sin x−2sin^2 x = 3sin x where −(π/2)≤x≤(π/2) . Find the sum of all posibble value of x.

$$\:\mathrm{Given}\:\mathrm{4cos}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{sin}\:\mathrm{x}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{3sin}\:\mathrm{x} \\ $$$$\mathrm{where}\:−\frac{\pi}{\mathrm{2}}\leqslant\mathrm{x}\leqslant\frac{\pi}{\mathrm{2}}\:.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of} \\ $$$$\mathrm{all}\:\mathrm{posibble}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}. \\ $$

Answered by MJS_new last updated on 22/Jan/21

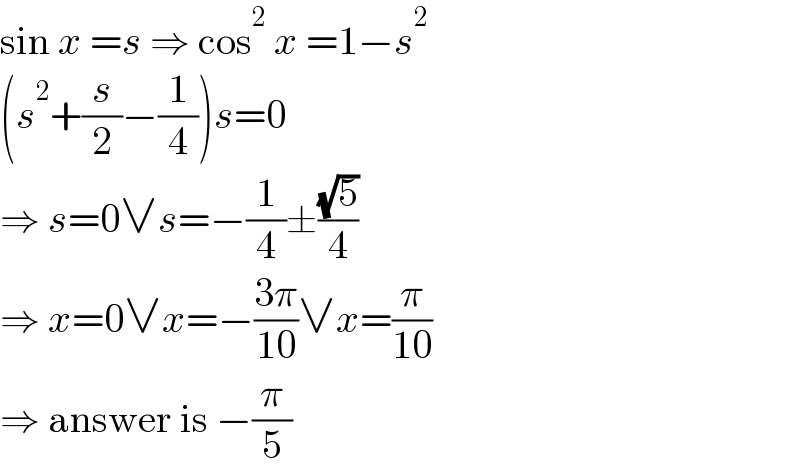
sin x =s ⇒ cos^2 x =1−s^2 (s^2 +(s/2)−(1/4))s=0 ⇒ s=0∨s=−(1/4)±((√5)/4) ⇒ x=0∨x=−((3π)/(10))∨x=(π/(10)) ⇒ answer is −(π/5)

$$\mathrm{sin}\:{x}\:={s}\:\Rightarrow\:\mathrm{cos}^{\mathrm{2}} \:{x}\:=\mathrm{1}−{s}^{\mathrm{2}} \\ $$$$\left({s}^{\mathrm{2}} +\frac{{s}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right){s}=\mathrm{0} \\ $$$$\Rightarrow\:{s}=\mathrm{0}\vee{s}=−\frac{\mathrm{1}}{\mathrm{4}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\Rightarrow\:{x}=\mathrm{0}\vee{x}=−\frac{\mathrm{3}\pi}{\mathrm{10}}\vee{x}=\frac{\pi}{\mathrm{10}} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:−\frac{\pi}{\mathrm{5}} \\ $$

Answered by Alepro3 last updated on 22/Jan/21

cos^2 x=1−sin^2 x ⇒ 4sin x−4sin^3 x−2sin^2 x=3sin x ⇒ sin x(4sin^2 x+2sin x−sin x)=0 ⇒ one solution is sin x=0 ⇒ x=kπ solving the 2^(nd) degree equation we have sin x_(1,2) =(−2±(√(4+16)))/8=(−1±(√5))/4 so x_(1,2) =sin^(−1) [(−1±(√5))/4]+2kπ and x_(3,4) =π−sin^(−1) [[(1−(√5))/4]+2kπ ⇒ the sum of all of this value of x is Σx=π+5kπ

$$ \\ $$$$\mathrm{cos}\:^{\mathrm{2}} {x}=\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\:\:\Rightarrow \\ $$$$\mathrm{4sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x}−\mathrm{2sin}\:^{\mathrm{2}} {x}=\mathrm{3sin}\:{x}\:\:\Rightarrow \\ $$$$\mathrm{sin}\:{x}\left(\mathrm{4sin}\:^{\mathrm{2}} {x}+\mathrm{2sin}\:{x}−\mathrm{sin}\:{x}\right)=\mathrm{0}\:\:\Rightarrow \\ $$$${one}\:{solution}\:{is}\:\mathrm{sin}\:{x}=\mathrm{0}\:\:\Rightarrow\:\:{x}={k}\pi \\ $$$${solving}\:{the}\:\mathrm{2}^{{nd}} {degree}\:{equation}\:{we}\:{have} \\ $$$$\mathrm{sin}\:{x}_{\mathrm{1},\mathrm{2}} =\left(−\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{16}}\right)/\mathrm{8}=\left(−\mathrm{1}\pm\sqrt{\mathrm{5}}\right)/\mathrm{4} \\ $$$${so}\:{x}_{\mathrm{1},\mathrm{2}} =\mathrm{sin}^{−\mathrm{1}} \left[\left(−\mathrm{1}\pm\sqrt{\mathrm{5}}\right)/\mathrm{4}\right]+\mathrm{2}{k}\pi\:\:{and}\:\:{x}_{\mathrm{3},\mathrm{4}} =\pi−\mathrm{sin}^{−\mathrm{1}} \left[\left[\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)/\mathrm{4}\right]+\mathrm{2}{k}\pi\:\:\Rightarrow\right. \\ $$$${the}\:{sum}\:{of}\:{all}\:{of}\:{this}\:{value}\:{of}\:{x}\:{is} \\ $$$$\Sigma{x}=\pi+\mathrm{5}{k}\pi \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com