
Question Number 10528 by Saham last updated on 16/Feb/17
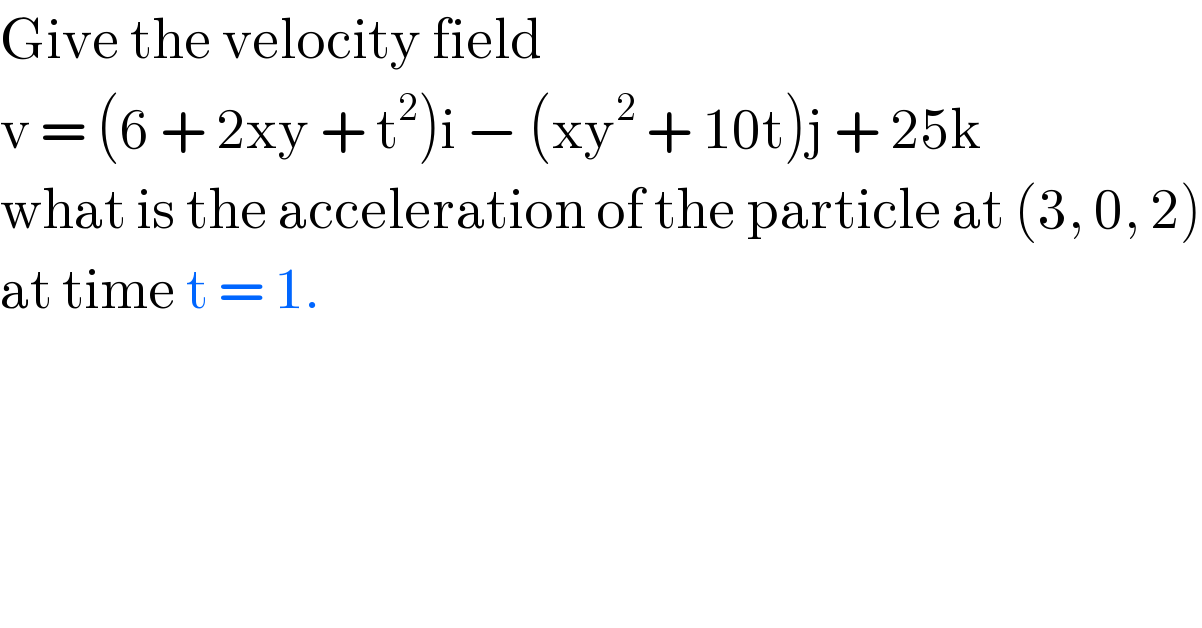
$$\mathrm{Give}\:\mathrm{the}\:\mathrm{velocity}\:\mathrm{field} \\ $$$$\mathrm{v}\:=\:\left(\mathrm{6}\:+\:\mathrm{2xy}\:+\:\mathrm{t}^{\mathrm{2}} \right)\mathrm{i}\:−\:\left(\mathrm{xy}^{\mathrm{2}} \:+\:\mathrm{10t}\right)\mathrm{j}\:+\:\mathrm{25k} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{the}\:\mathrm{particle}\:\mathrm{at}\:\left(\mathrm{3},\:\mathrm{0},\:\mathrm{2}\right) \\ $$$$\mathrm{at}\:\mathrm{time}\:\mathrm{t}\:=\:\mathrm{1}. \\ $$
Answered by robocop last updated on 16/Feb/17

$${v}=\mathrm{18}+\mathrm{6}{xy}+\mathrm{3}+\mathrm{50} \\ $$$${a}={v}' \\ $$$${a}=\mathrm{6}\left({x}+{y}\right) \\ $$
Commented by Saham last updated on 16/Feb/17

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by FilupS last updated on 18/Feb/17

$$\mathrm{incorrect}.\:\mathrm{you}\:\mathrm{are}\:\mathrm{refering}\:\mathrm{to} \\ $$$$\mathrm{linear}\:\mathrm{velocity} \\ $$$$\mathrm{i}.\mathrm{e}.\:\:\:{v}\in\mathbb{R} \\ $$$$\mathrm{This}\:\mathrm{question}\:\mathrm{is}\:\mathrm{about}\:\mathrm{a}\:\mathrm{particle}\:\mathrm{in}\:\mathrm{a}\:\mathrm{field} \\ $$$$\mathrm{i}.\mathrm{e}.\:{v}\in\mathbb{R}^{\mathrm{3}} \\ $$
Answered by ajfour last updated on 16/Feb/17
![a_x =2(yv_x +xv_y +t); at that time and place is =2[0+3(−10)+1]=−58 a_y =−(y^2 v_x +2xyv_y +10); then and there will be =−[0+0+10]=−10 a_z =0 So a^� then and there (3,0,2,1) would be −58i^� −10j^� .](Q10531.png)
$${a}_{{x}} =\mathrm{2}\left({yv}_{{x}} +{xv}_{{y}} +{t}\right);\:{at}\:{that}\:{time}\:{and}\:{place}\:{is}\:=\mathrm{2}\left[\mathrm{0}+\mathrm{3}\left(−\mathrm{10}\right)+\mathrm{1}\right]=−\mathrm{58} \\ $$$${a}_{{y}} =−\left({y}^{\mathrm{2}} {v}_{{x}} +\mathrm{2}{xyv}_{{y}} +\mathrm{10}\right);\:{then}\:{and}\:{there}\:{will}\:{be}\:=−\left[\mathrm{0}+\mathrm{0}+\mathrm{10}\right]=−\mathrm{10} \\ $$$${a}_{{z}} =\mathrm{0} \\ $$$${So}\:\bar {{a}}\:{then}\:{and}\:{there}\:\left(\mathrm{3},\mathrm{0},\mathrm{2},\mathrm{1}\right)\:{would}\:{be}\:−\mathrm{58}\hat {{i}}−\mathrm{10}\hat {{j}}. \\ $$
Commented by Saham last updated on 16/Feb/17

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Answered by mrW1 last updated on 16/Feb/17
![v_x =6+2xy+t^2 v_y =−(xy^2 +10t) v_z =25 a_x =(dv_x /dt)=2x(dy/dt)+2y(dx/dt)+2t=2(xv_y +yv_x +t) a_y =(dv_y /dt)=−(xy(dy/dt)+y^2 (dx/dt)+10)=−(xyv_y +y^2 v_x +10) a_z =0 at (3,0,2) and t=1: v_x =6+2×3×0+1^2 =7 v_y =−(3×0^2 +10×1)=−10 v_z =25 a_x =2[3×(−10)+0×7+1]=−58 a_y =−[3×0×(−10)+0^2 ×7+10]=−10 a_z =0 ⇒a=−58i−10j+0k](Q10532.png)
$${v}_{{x}} =\mathrm{6}+\mathrm{2}{xy}+{t}^{\mathrm{2}} \\ $$$${v}_{{y}} =−\left({xy}^{\mathrm{2}} +\mathrm{10}{t}\right) \\ $$$${v}_{{z}} =\mathrm{25} \\ $$$${a}_{{x}} =\frac{{dv}_{{x}} }{{dt}}=\mathrm{2}{x}\frac{{dy}}{{dt}}+\mathrm{2}{y}\frac{{dx}}{{dt}}+\mathrm{2}{t}=\mathrm{2}\left({xv}_{{y}} +{yv}_{{x}} +{t}\right) \\ $$$${a}_{{y}} =\frac{{dv}_{{y}} }{{dt}}=−\left({xy}\frac{{dy}}{{dt}}+{y}^{\mathrm{2}} \frac{{dx}}{{dt}}+\mathrm{10}\right)=−\left({xyv}_{{y}} +{y}^{\mathrm{2}} {v}_{{x}} +\mathrm{10}\right) \\ $$$${a}_{{z}} =\mathrm{0} \\ $$$$ \\ $$$${at}\:\left(\mathrm{3},\mathrm{0},\mathrm{2}\right)\:{and}\:{t}=\mathrm{1}: \\ $$$${v}_{{x}} =\mathrm{6}+\mathrm{2}×\mathrm{3}×\mathrm{0}+\mathrm{1}^{\mathrm{2}} =\mathrm{7} \\ $$$${v}_{{y}} =−\left(\mathrm{3}×\mathrm{0}^{\mathrm{2}} +\mathrm{10}×\mathrm{1}\right)=−\mathrm{10} \\ $$$${v}_{{z}} =\mathrm{25} \\ $$$${a}_{{x}} =\mathrm{2}\left[\mathrm{3}×\left(−\mathrm{10}\right)+\mathrm{0}×\mathrm{7}+\mathrm{1}\right]=−\mathrm{58} \\ $$$${a}_{{y}} =−\left[\mathrm{3}×\mathrm{0}×\left(−\mathrm{10}\right)+\mathrm{0}^{\mathrm{2}} ×\mathrm{7}+\mathrm{10}\right]=−\mathrm{10} \\ $$$${a}_{{z}} =\mathrm{0} \\ $$$$\Rightarrow{a}=−\mathrm{58}{i}−\mathrm{10}{j}+\mathrm{0}{k} \\ $$
Commented by Saham last updated on 16/Feb/17

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
