
Previous in Relation and Functions Next in Relation and Functions
Question Number 11196 by agni5 last updated on 16/Mar/17
![Give an example each with justification,of a function defined by ]−1,1[ ,which is 1)one one but not onto. 2)onto but not one one.](Q11196.png)
$$\mathrm{Give}\:\mathrm{an}\:\mathrm{example}\:\mathrm{each}\:\mathrm{with}\:\mathrm{justification},\mathrm{of}\:\mathrm{a}\:\mathrm{function} \\ $$$$\left.\mathrm{defined}\:\mathrm{by}\:\right]−\mathrm{1},\mathrm{1}\left[\:,\mathrm{which}\:\mathrm{is}\right. \\ $$$$\left.\mathrm{1}\right)\mathrm{one}\:\mathrm{one}\:\mathrm{but}\:\mathrm{not}\:\mathrm{onto}. \\ $$$$\left.\mathrm{2}\right)\mathrm{onto}\:\mathrm{but}\:\mathrm{not}\:\mathrm{one}\:\mathrm{one}. \\ $$
Commented by FilupS last updated on 16/Mar/17
![I don′t understand the question. Are you looking for ∀x:f(x)∈[−1,1]?](Q11201.png)
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{question}. \\ $$$$ \\ $$$$\mathrm{Are}\:\mathrm{you}\:\mathrm{looking}\:\mathrm{for}\:\:\forall{x}:{f}\left({x}\right)\in\left[−\mathrm{1},\mathrm{1}\right]? \\ $$
Commented by agni5 last updated on 16/Mar/17
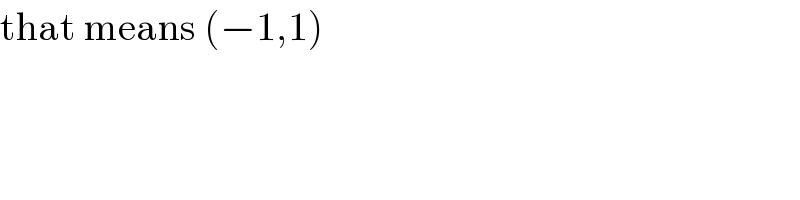
$$\mathrm{that}\:\mathrm{means}\:\left(−\mathrm{1},\mathrm{1}\right) \\ $$
