
Question Number 49116 by hassentimol last updated on 03/Dec/18
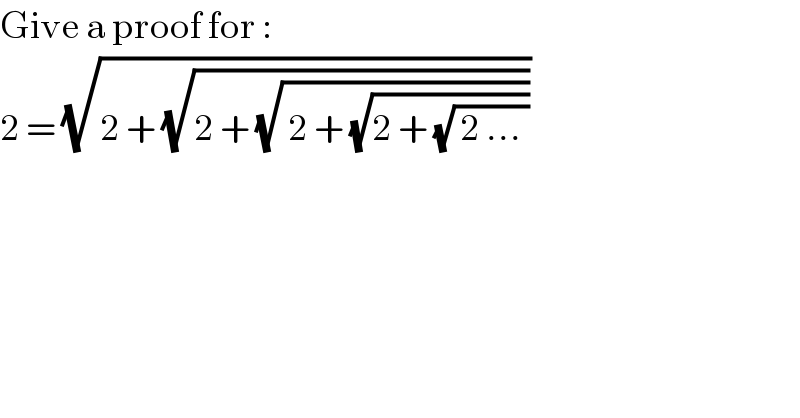
$$\mathrm{Give}\:\mathrm{a}\:\mathrm{proof}\:\mathrm{for}\:: \\ $$$$\mathrm{2}\:=\:\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}\:+\:\sqrt{\:\mathrm{2}\:+\:\sqrt{\mathrm{2}\:+\:\sqrt{\:\mathrm{2}\:...\:}}}}} \\ $$
Commented by maxmathsup by imad last updated on 03/Dec/18
![let u_(n+1) =(√(2+u_n )) with n≥0 and u_o =(√2) ⇒u_(n+1) =f(u_n ) with f(x)=(√(2+x)) we prove by recurrence that u_n >0 we have for x>0 f^′ (x)=(1/(2(√(2+x))))>0 so f is increasing on [0,+∞[ let w(x)=x−f(x) ⇒ w^′ (x)=1−f^′ (x)=1−(1/(2(√(2+x)))) =((2(√(2+x))−1)/(2(√(2+x)))) >0 ⇒w is increasing on [0,+∞[ we have w(1) =1−f(1)=1−(√3)<0 w(3)=3−f(3)=3−(√5)>0 ⇒ ∃! x_0 ∈]1,3[ / w(x_0 )=0 we verify that x_0 =2 if l=lim_(n→+∞) u_n we get f(l)=l ⇒ l =x_0 =2 .](Q49146.png)
$${let}\:{u}_{{n}+\mathrm{1}} =\sqrt{\mathrm{2}+{u}_{{n}} }\:\:{with}\:{n}\geqslant\mathrm{0}\:{and}\:{u}_{{o}} =\sqrt{\mathrm{2}}\:\:\Rightarrow{u}_{{n}+\mathrm{1}} ={f}\left({u}_{{n}} \right)\:{with}\:{f}\left({x}\right)=\sqrt{\mathrm{2}+{x}} \\ $$$${we}\:{prove}\:{by}\:{recurrence}\:{that}\:{u}_{{n}} >\mathrm{0}\:\:{we}\:{have}\:{for}\:{x}>\mathrm{0}\:{f}^{'} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}+{x}}}>\mathrm{0}\:{so} \\ $$$${f}\:{is}\:{increasing}\:{on}\:\left[\mathrm{0},+\infty\left[\:\:{let}\:{w}\left({x}\right)={x}−{f}\left({x}\right)\:\Rightarrow\right.\right. \\ $$$${w}^{'} \left({x}\right)=\mathrm{1}−{f}^{'} \left({x}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}+{x}}}\:=\frac{\mathrm{2}\sqrt{\mathrm{2}+{x}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}+{x}}}\:>\mathrm{0}\:\Rightarrow{w}\:{is}\:{increasing}\:{on}\:\left[\mathrm{0},+\infty\left[\right.\right. \\ $$$$\left.{we}\:{have}\:{w}\left(\mathrm{1}\right)\:=\mathrm{1}−{f}\left(\mathrm{1}\right)=\mathrm{1}−\sqrt{\mathrm{3}}<\mathrm{0}\:\:\:\:{w}\left(\mathrm{3}\right)=\mathrm{3}−{f}\left(\mathrm{3}\right)=\mathrm{3}−\sqrt{\mathrm{5}}>\mathrm{0}\:\Rightarrow\:\exists!\:{x}_{\mathrm{0}} \in\right]\mathrm{1},\mathrm{3}\left[\right. \\ $$$$/\:{w}\left({x}_{\mathrm{0}} \right)=\mathrm{0}\:\:\:\:{we}\:{verify}\:{that}\:{x}_{\mathrm{0}} =\mathrm{2}\:\:\:{if}\:{l}={lim}_{{n}\rightarrow+\infty} {u}_{{n}} \:{we}\:{get}\:{f}\left({l}\right)={l}\:\Rightarrow \\ $$$${l}\:={x}_{\mathrm{0}} =\mathrm{2}\:. \\ $$$$ \\ $$
Commented by hassentimol last updated on 10/Dec/18

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Dec/18
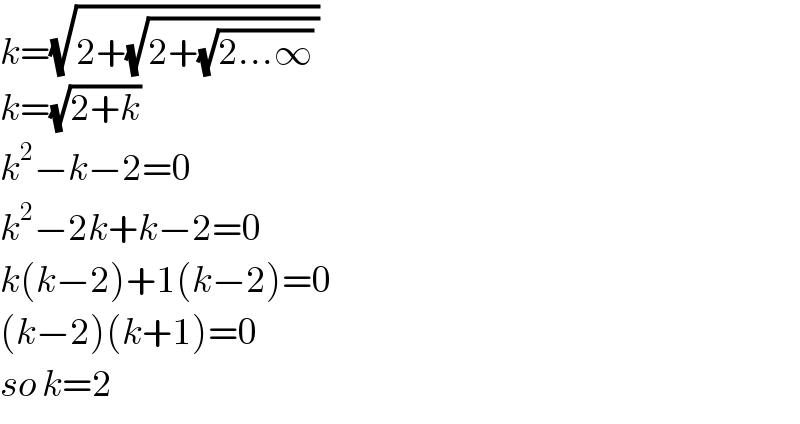
$${k}=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}...\infty}\:}} \\ $$$${k}=\sqrt{\mathrm{2}+{k}}\: \\ $$$${k}^{\mathrm{2}} −{k}−\mathrm{2}=\mathrm{0} \\ $$$${k}^{\mathrm{2}} −\mathrm{2}{k}+{k}−\mathrm{2}=\mathrm{0} \\ $$$${k}\left({k}−\mathrm{2}\right)+\mathrm{1}\left({k}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\left({k}−\mathrm{2}\right)\left({k}+\mathrm{1}\right)=\mathrm{0} \\ $$$${so}\:{k}=\mathrm{2}\:\: \\ $$
