
Question Number 194881 by tri26112004 last updated on 18/Jul/23
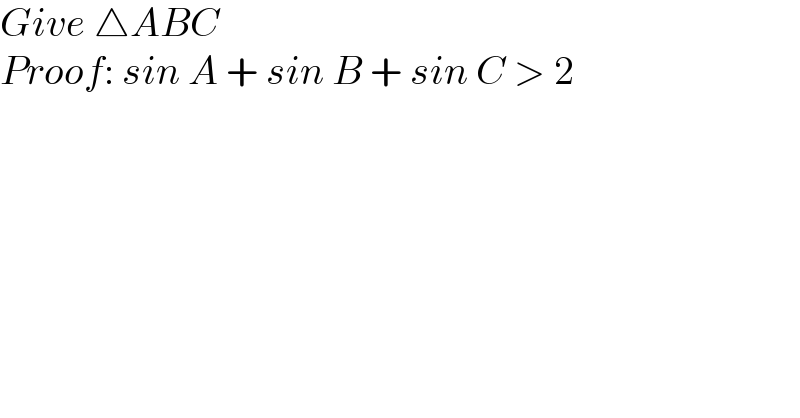
$${Give}\:\bigtriangleup{ABC}\: \\ $$$${Proof}:\:{sin}\:{A}\:+\:{sin}\:{B}\:+\:{sin}\:{C}\:>\:\mathrm{2} \\ $$
Answered by Frix last updated on 19/Jul/23
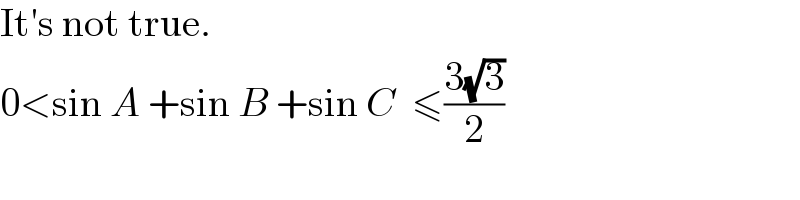
$$\mathrm{It}'\mathrm{s}\:\mathrm{not}\:\mathrm{true}. \\ $$$$\mathrm{0}<\mathrm{sin}\:{A}\:+\mathrm{sin}\:{B}\:+\mathrm{sin}\:{C}\:\:\leqslant\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Commented by tri26112004 last updated on 19/Jul/23
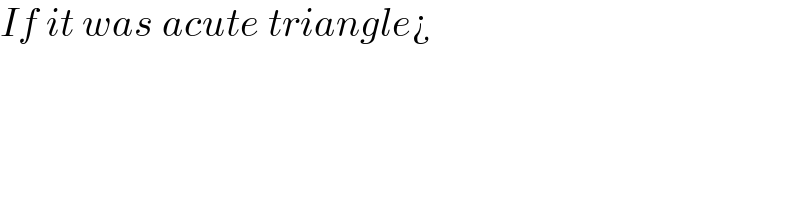
$${If}\:{it}\:{was}\:{acute}\:{triangle}¿ \\ $$
