Question and Answers Forum

All Questions Topic List

GeometryQuestion and Answers: Page 99

Question Number 45427 Answers: 0 Comments: 4

Question Number 45381 Answers: 0 Comments: 1

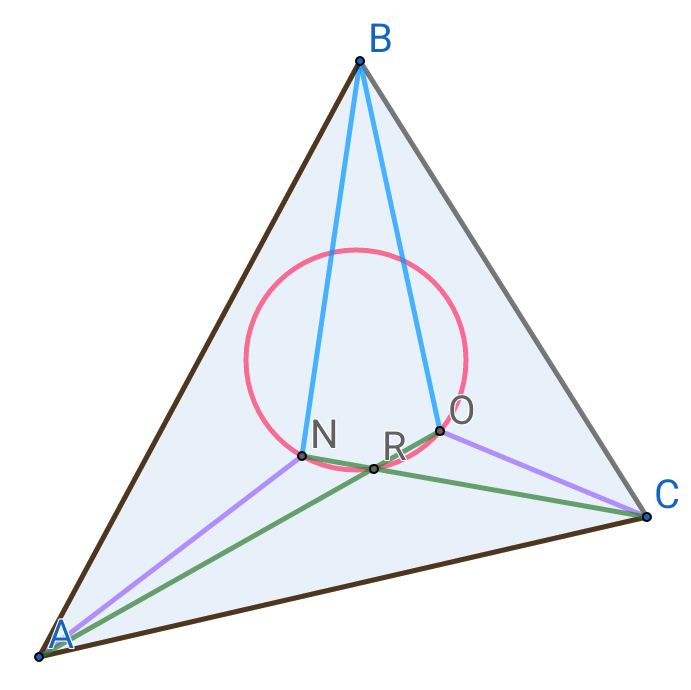
Question Number 45366 Answers: 2 Comments: 2

Question Number 45187 Answers: 1 Comments: 6

Question Number 45122 Answers: 0 Comments: 1

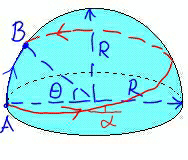
Question Number 44950 Answers: 1 Comments: 4

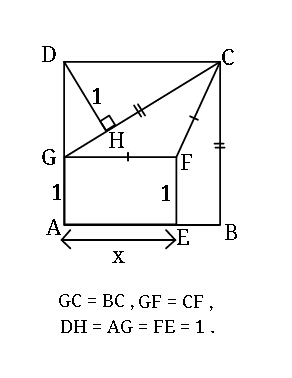
Question Number 44929 Answers: 2 Comments: 1

Question Number 44636 Answers: 1 Comments: 0

Question Number 44621 Answers: 2 Comments: 0

Question Number 44548 Answers: 0 Comments: 0

(a) The area of a sector of a circle of radius 12cm is 132cm^2 . If the sector is folded such that its straight edges coincide to form a cone. Find the radius of the base of the cone [ Take π = ((22)/7) ] . (b) A circle of centre O has radius 5cm. A chord PQ of the circle is 6cm long. caclculate: (i) The distance of the chord from the centre O (ii) The angle POQ

$$\left(\mathrm{a}\right) \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{a}\:\mathrm{sector}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{radius}\:\:\mathrm{12cm}\:\mathrm{is}\:\:\mathrm{132cm}^{\mathrm{2}} \:.\:\:\mathrm{If}\:\mathrm{the}\:\mathrm{sector} \\ $$$$\mathrm{is}\:\mathrm{folded}\:\mathrm{such}\:\mathrm{that}\:\mathrm{its}\:\mathrm{straight}\:\mathrm{edges}\:\mathrm{coincide}\:\mathrm{to}\:\mathrm{form}\:\mathrm{a}\:\mathrm{cone}.\:\mathrm{Find}\:\mathrm{the}\: \\ $$$$\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{base}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cone}\:\:\:\:\left[\:\:\mathrm{Take}\:\:\:\:\pi\:\:=\:\:\frac{\mathrm{22}}{\mathrm{7}}\:\right]\:. \\ $$$$ \\ $$$$\left(\mathrm{b}\right)\:\:\: \\ $$$$\mathrm{A}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{centre}\:\mathrm{O}\:\mathrm{has}\:\mathrm{radius}\:\mathrm{5cm}.\:\:\mathrm{A}\:\mathrm{chord}\:\mathrm{PQ}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{is}\:\mathrm{6cm}\:\mathrm{long}. \\ $$$$\mathrm{caclculate}: \\ $$$$\:\:\:\:\left(\mathrm{i}\right)\:\:\:\mathrm{The}\:\mathrm{distance}\:\mathrm{of}\:\mathrm{the}\:\mathrm{chord}\:\mathrm{from}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{O} \\ $$$$\:\:\:\left(\mathrm{ii}\right)\:\:\mathrm{The}\:\mathrm{angle}\:\mathrm{POQ} \\ $$

Question Number 44497 Answers: 0 Comments: 8

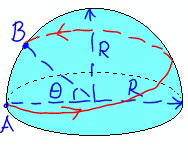
Question Number 44479 Answers: 1 Comments: 5

Question Number 44430 Answers: 0 Comments: 0

Question Number 44395 Answers: 1 Comments: 3

Question Number 44365 Answers: 2 Comments: 1

Question Number 44336 Answers: 0 Comments: 0

Question Number 44103 Answers: 1 Comments: 1

Question Number 44017 Answers: 1 Comments: 3

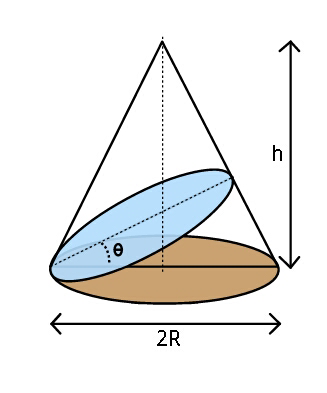
Question Number 43980 Answers: 1 Comments: 0

Question Number 43944 Answers: 1 Comments: 0

If the points (−3, 5) , (4, −2) and (6, 2) are the vertices of a triangle. (i) Find the equation of the perpendicular bisector of the sides (ii) Find the coordinate of the circumcenter. (The circumcenter of a triangle is the point of intersection of the perpendicular bisector of the side (iii) Find the radius of the circumcircle.

Question Number 43834 Answers: 0 Comments: 3

Question Number 43825 Answers: 2 Comments: 0

Question Number 43621 Answers: 1 Comments: 2

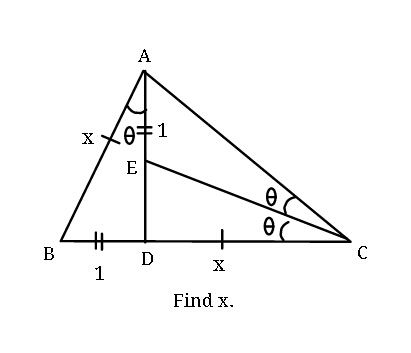
Question Number 43465 Answers: 2 Comments: 1

Question Number 43461 Answers: 0 Comments: 1

found something (others have found before) which I thought might be of interest, especially for Sir Tanmay Chaudhury: take any polynome of degree 4 with 2 real inflection points y=ax^4 +bx^3 +cx^2 +dx+e y′′=12ax^2 +6bx+2c=0 has got 2 real solutions x_1 and x_2 the line connecting the inflection points intersects the curve in 2 more points P and Q, their x−values are p and q let p<x_1 <x_2 <q ⇒ ((x_2 −x_1 )/(x_1 −p))=((x_2 −x_1 )/(q−x_2 ))=(1/2)+((√5)/2) which is the Golden Ratio

$$\mathrm{found}\:\mathrm{something}\:\left(\mathrm{others}\:\mathrm{have}\:\mathrm{found}\:\mathrm{before}\right) \\ $$$$\mathrm{which}\:\mathrm{I}\:\mathrm{thought}\:\mathrm{might}\:\mathrm{be}\:\mathrm{of}\:\mathrm{interest}, \\ $$$$\mathrm{especially}\:\mathrm{for}\:\mathrm{Sir}\:\mathrm{Tanmay}\:\mathrm{Chaudhury}: \\ $$$$\mathrm{take}\:\mathrm{any}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{4}\:\mathrm{with}\:\mathrm{2}\:\mathrm{real} \\ $$$$\mathrm{inflection}\:\mathrm{points} \\ $$$${y}={ax}^{\mathrm{4}} +{bx}^{\mathrm{3}} +{cx}^{\mathrm{2}} +{dx}+{e} \\ $$$${y}''=\mathrm{12}{ax}^{\mathrm{2}} +\mathrm{6}{bx}+\mathrm{2}{c}=\mathrm{0}\:\mathrm{has}\:\mathrm{got}\:\mathrm{2}\:\mathrm{real}\:\mathrm{solutions} \\ $$$${x}_{\mathrm{1}} \:\mathrm{and}\:{x}_{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{line}\:\mathrm{connecting}\:\mathrm{the}\:\mathrm{inflection}\:\mathrm{points} \\ $$$$\mathrm{intersects}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{in}\:\mathrm{2}\:\mathrm{more}\:\mathrm{points} \\ $$$${P}\:\mathrm{and}\:{Q},\:\mathrm{their}\:{x}−\mathrm{values}\:\mathrm{are}\:{p}\:\mathrm{and}\:{q} \\ $$$$\mathrm{let}\:{p}<{x}_{\mathrm{1}} <{x}_{\mathrm{2}} <{q} \\ $$$$\Rightarrow\:\frac{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }{{x}_{\mathrm{1}} −{p}}=\frac{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }{{q}−{x}_{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{which}\:\mathrm{is}\:\mathrm{the}\:\mathrm{Golden}\:\mathrm{Ratio} \\ $$

Question Number 43360 Answers: 0 Comments: 9

Pg 94 Pg 95 Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103

Contact: info@tinkutara.com