
GeometryQuestion and Answers: Page 94
Question Number 52426 Answers: 2 Comments: 1

Question Number 52409 Answers: 1 Comments: 1

Question Number 52360 Answers: 1 Comments: 1

Question Number 52321 Answers: 0 Comments: 0
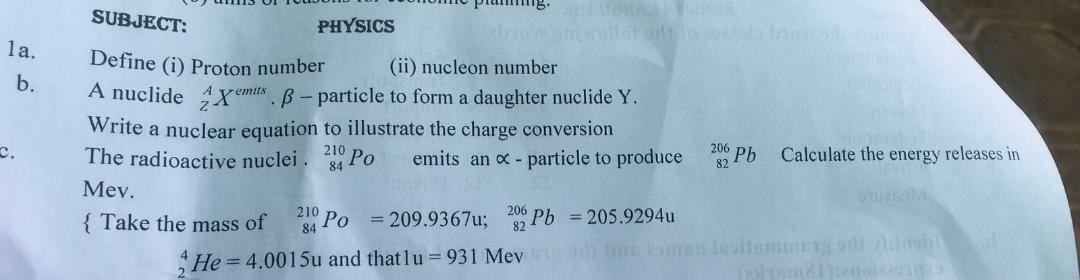
Question Number 52261 Answers: 0 Comments: 9
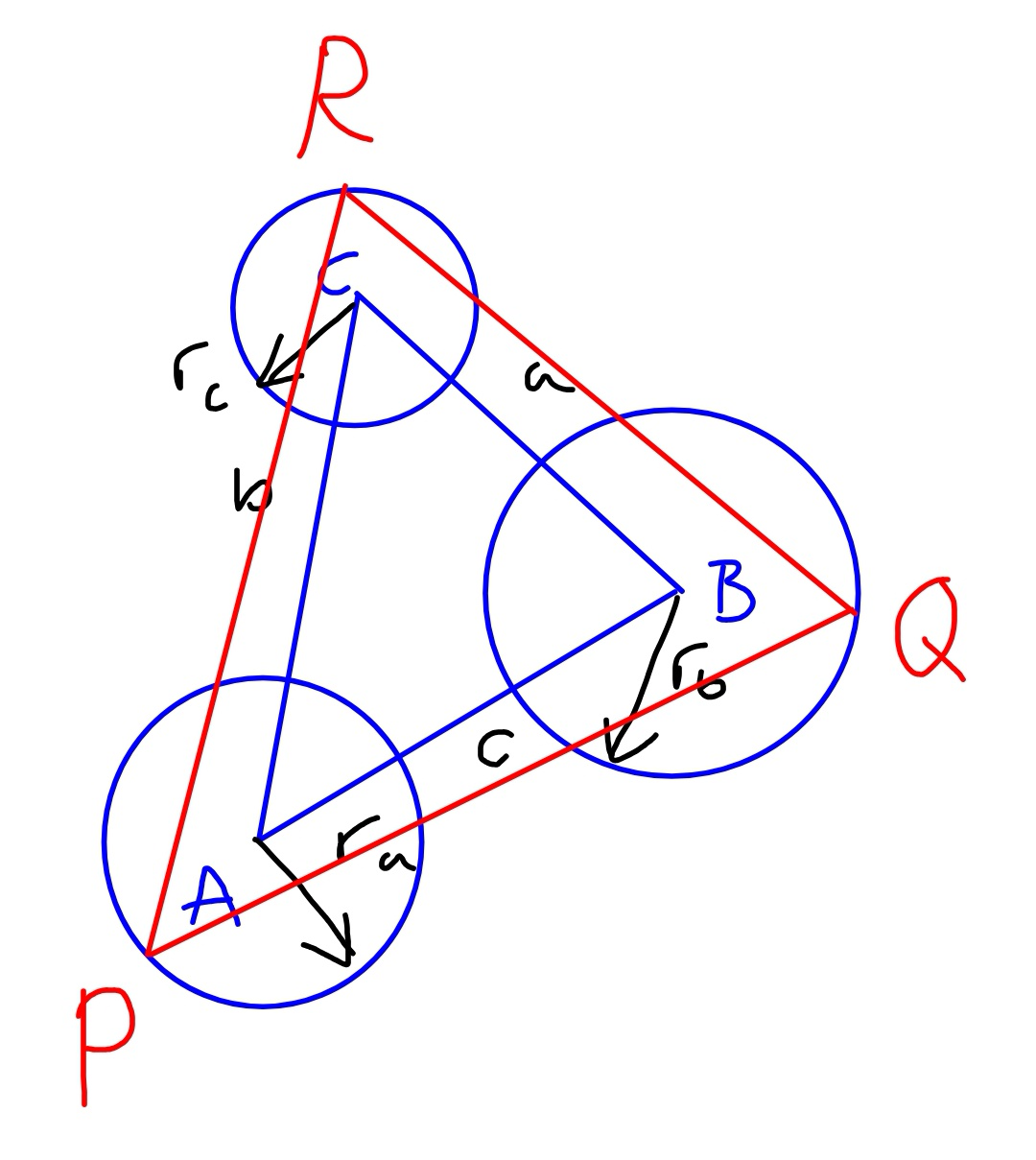
Question Number 52198 Answers: 2 Comments: 0

Question Number 52182 Answers: 0 Comments: 1
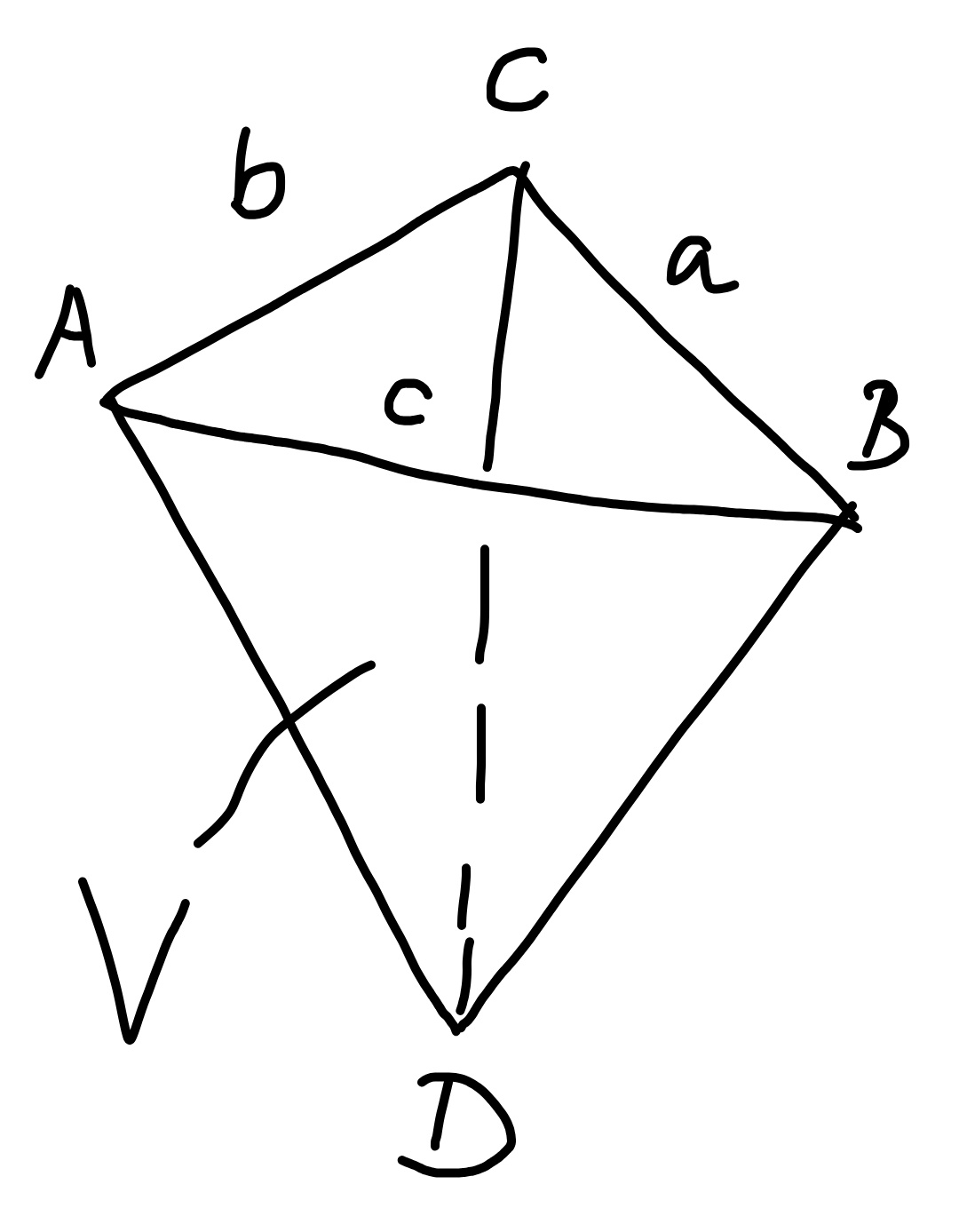
Question Number 52190 Answers: 2 Comments: 3

Question Number 52129 Answers: 1 Comments: 5

Question Number 52061 Answers: 2 Comments: 3
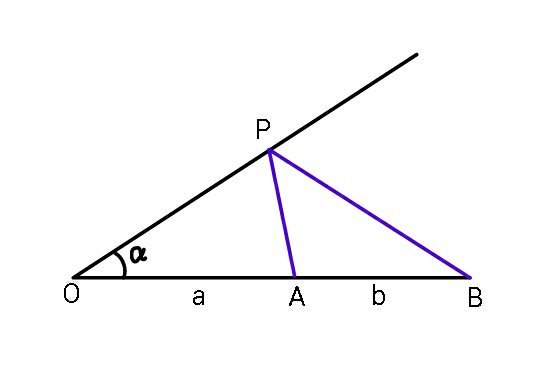
Question Number 52052 Answers: 0 Comments: 1

Question Number 52016 Answers: 1 Comments: 1
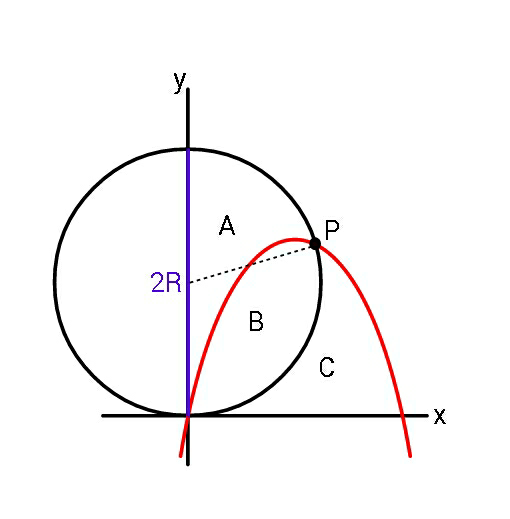
Question Number 52012 Answers: 0 Comments: 2

Question Number 51973 Answers: 0 Comments: 1
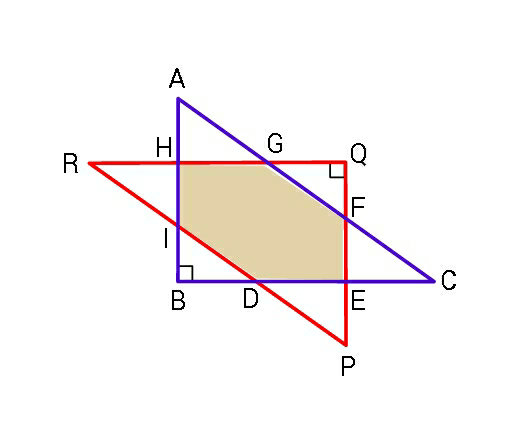
Question Number 51942 Answers: 1 Comments: 5

Question Number 51911 Answers: 0 Comments: 2

Question Number 51905 Answers: 2 Comments: 0
Question Number 51884 Answers: 1 Comments: 4

Question Number 51849 Answers: 3 Comments: 3
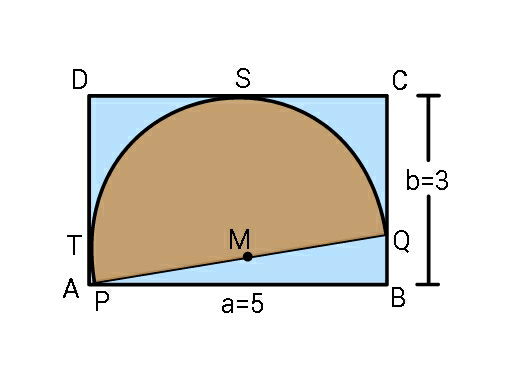
Question Number 51700 Answers: 1 Comments: 1
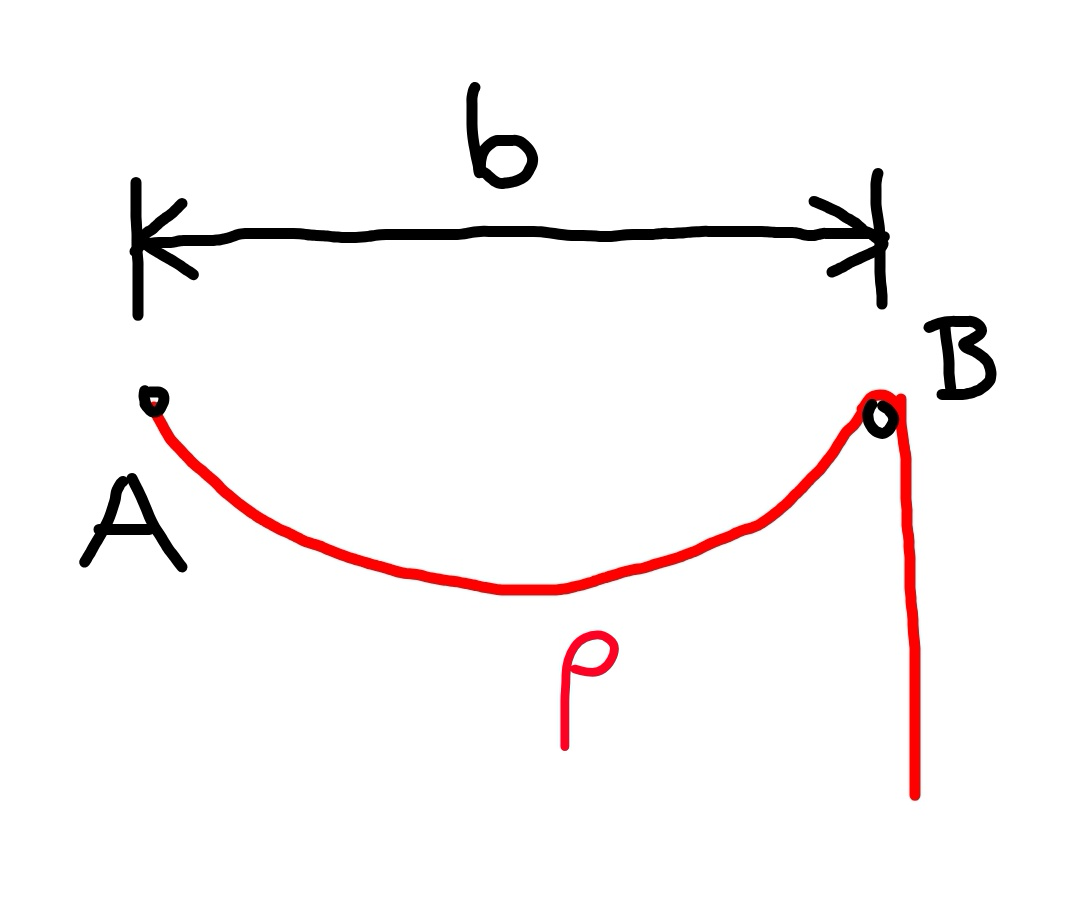
Question Number 51658 Answers: 3 Comments: 7

Question Number 51636 Answers: 1 Comments: 4

Question Number 51644 Answers: 0 Comments: 0

Question Number 51605 Answers: 0 Comments: 0

Question Number 51558 Answers: 1 Comments: 3

Question Number 51549 Answers: 0 Comments: 0
