GeometryQuestion and Answers: Page 92
Question Number 58686 Answers: 0 Comments: 1

Question Number 58567 Answers: 0 Comments: 1
Question Number 58512 Answers: 1 Comments: 1
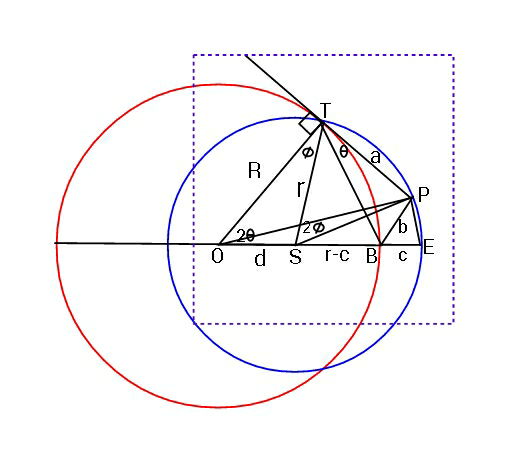
Question Number 58493 Answers: 1 Comments: 0

Question Number 58282 Answers: 1 Comments: 0
Question Number 57949 Answers: 0 Comments: 0
Question Number 57310 Answers: 0 Comments: 1
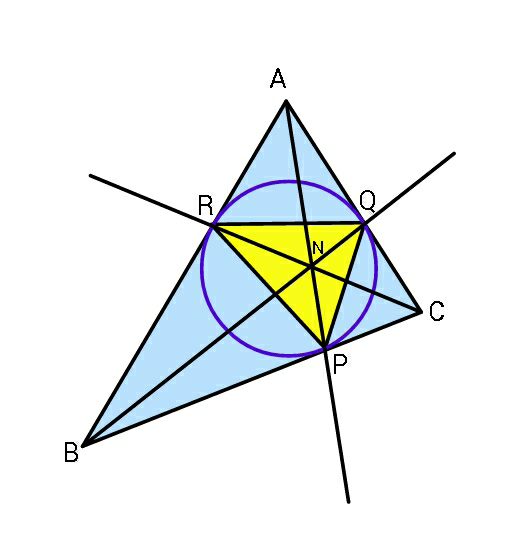
Question Number 57296 Answers: 1 Comments: 1
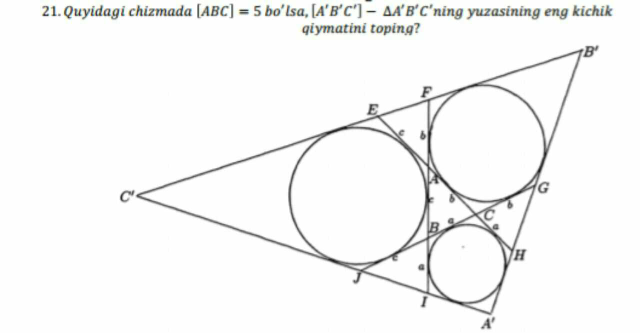
Question Number 57283 Answers: 1 Comments: 1

Question Number 57186 Answers: 1 Comments: 3

Question Number 57198 Answers: 0 Comments: 2

Question Number 56986 Answers: 2 Comments: 1

Question Number 56838 Answers: 1 Comments: 0
Question Number 56639 Answers: 0 Comments: 1

Question Number 56289 Answers: 1 Comments: 7
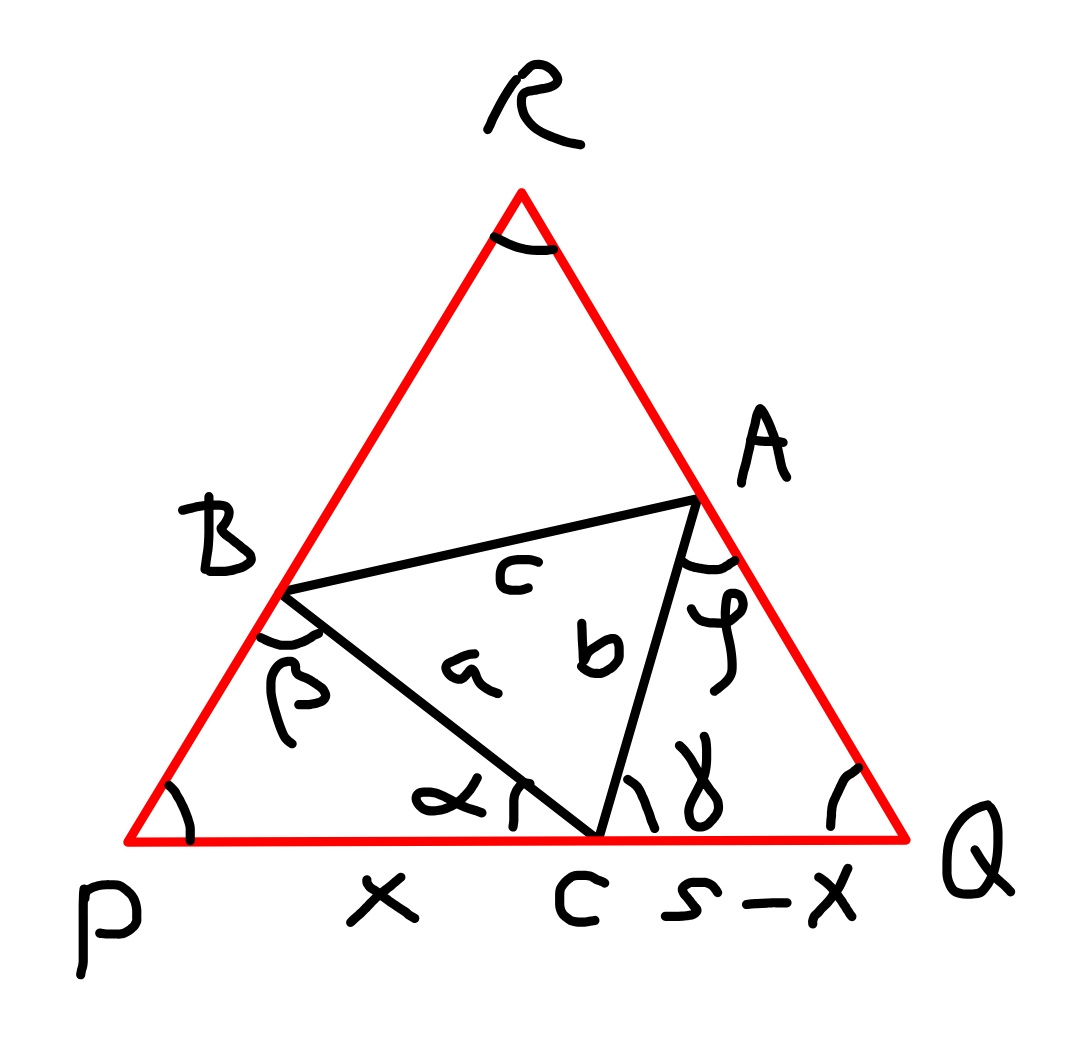
Question Number 56037 Answers: 1 Comments: 5

Question Number 55820 Answers: 0 Comments: 7

Question Number 55475 Answers: 1 Comments: 0
Question Number 55044 Answers: 1 Comments: 2
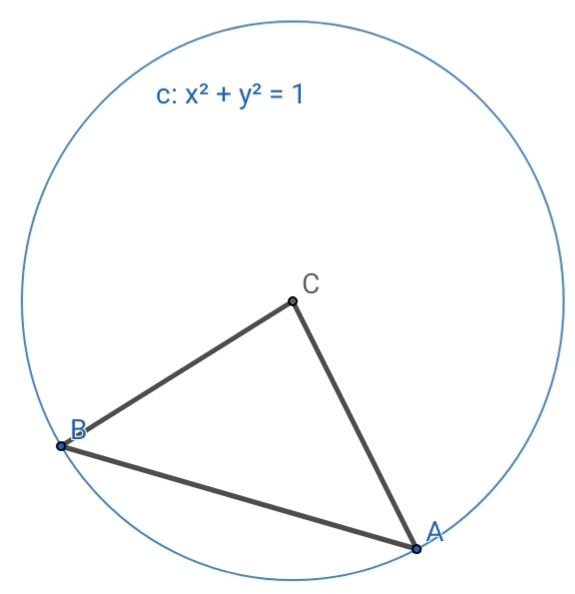
Question Number 54991 Answers: 0 Comments: 3
Question Number 54788 Answers: 2 Comments: 1
Question Number 54661 Answers: 1 Comments: 3

Question Number 54602 Answers: 0 Comments: 1
Question Number 54487 Answers: 0 Comments: 0

Question Number 58313 Answers: 2 Comments: 2
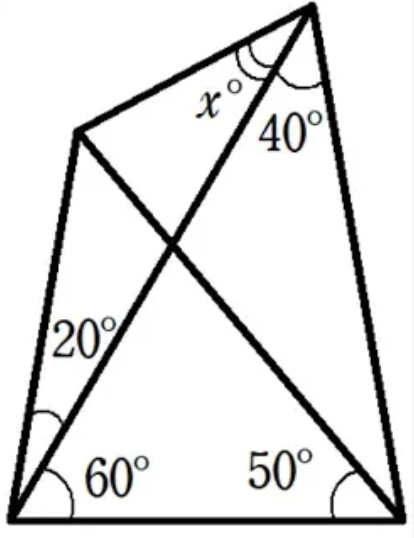
Question Number 54312 Answers: 1 Comments: 2