
GeometryQuestion and Answers: Page 91
Question Number 60888 Answers: 1 Comments: 1
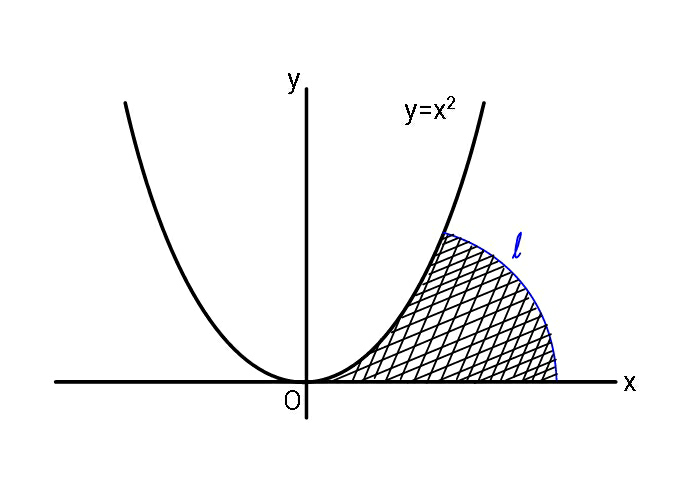
Question Number 61612 Answers: 0 Comments: 7
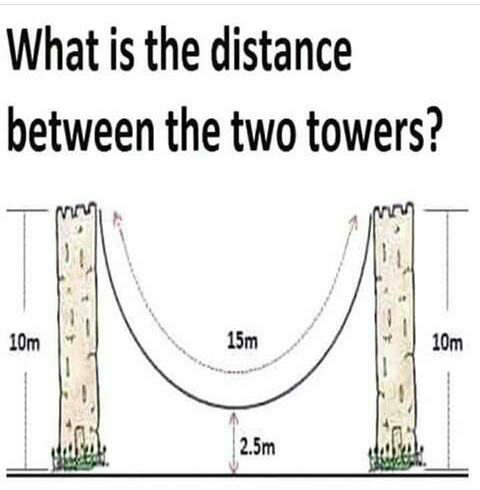
Question Number 60647 Answers: 0 Comments: 3

Question Number 60588 Answers: 0 Comments: 1
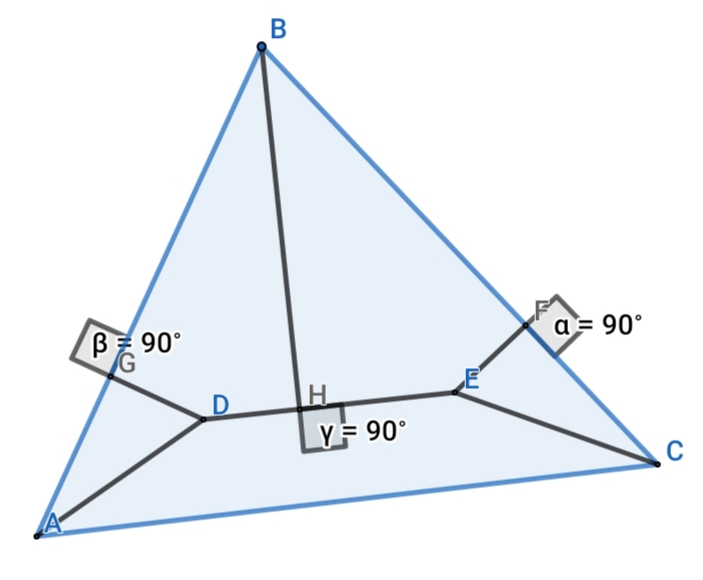
Question Number 60527 Answers: 2 Comments: 1
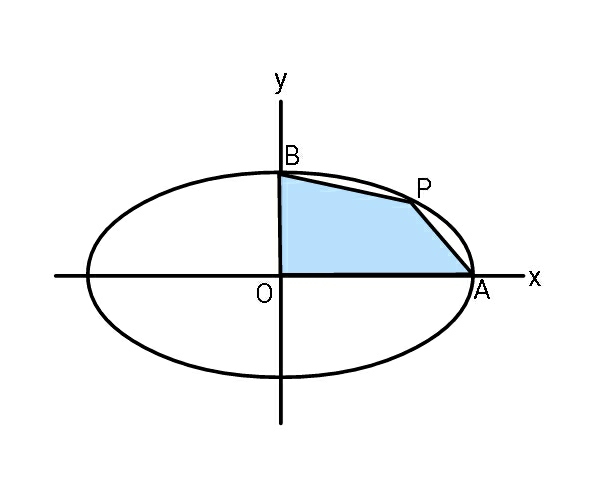
Question Number 60313 Answers: 3 Comments: 1
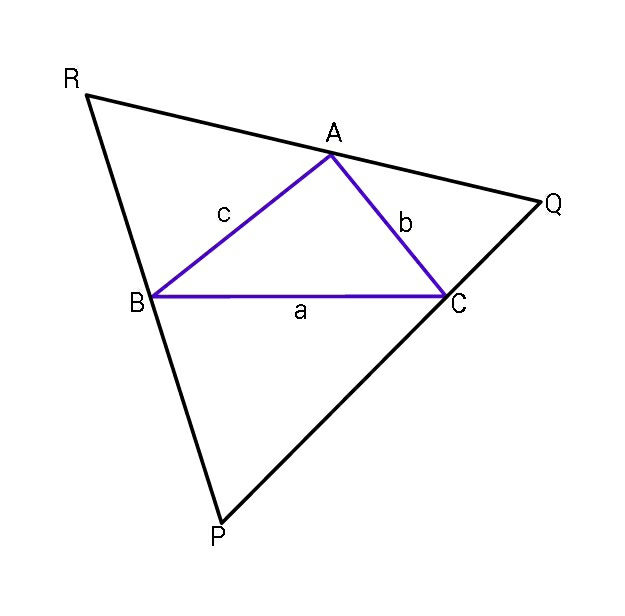
Question Number 60283 Answers: 1 Comments: 1
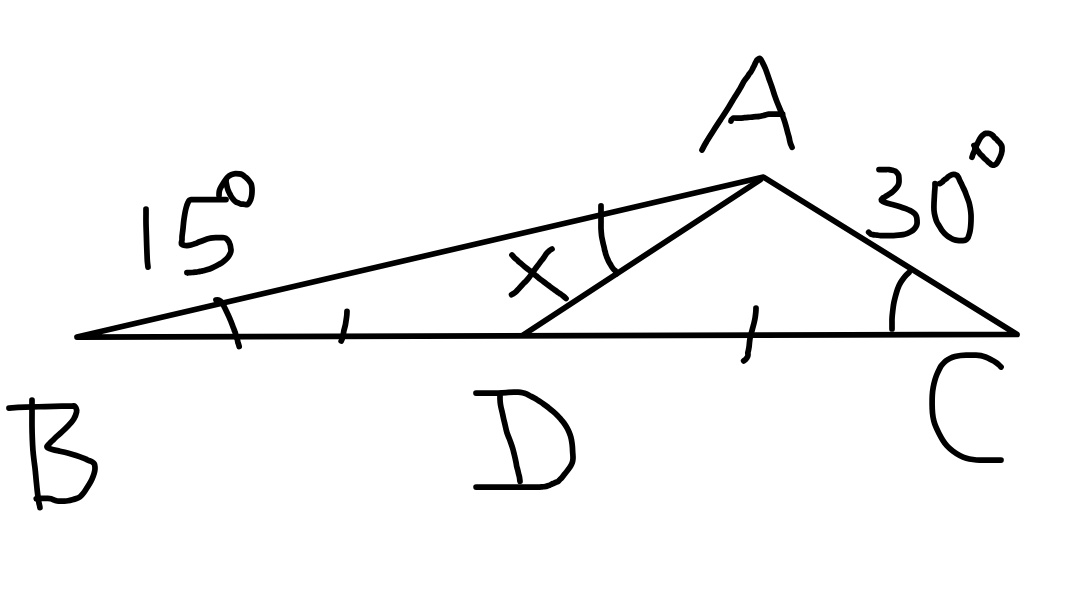
Question Number 60241 Answers: 0 Comments: 1

Question Number 60238 Answers: 0 Comments: 0

Question Number 60085 Answers: 1 Comments: 4

Question Number 60058 Answers: 1 Comments: 1

Question Number 59987 Answers: 0 Comments: 0

Question Number 59700 Answers: 0 Comments: 5

Question Number 59620 Answers: 1 Comments: 2

Question Number 59287 Answers: 1 Comments: 0
Question Number 59181 Answers: 1 Comments: 1

Question Number 59100 Answers: 1 Comments: 4

Question Number 59018 Answers: 0 Comments: 1
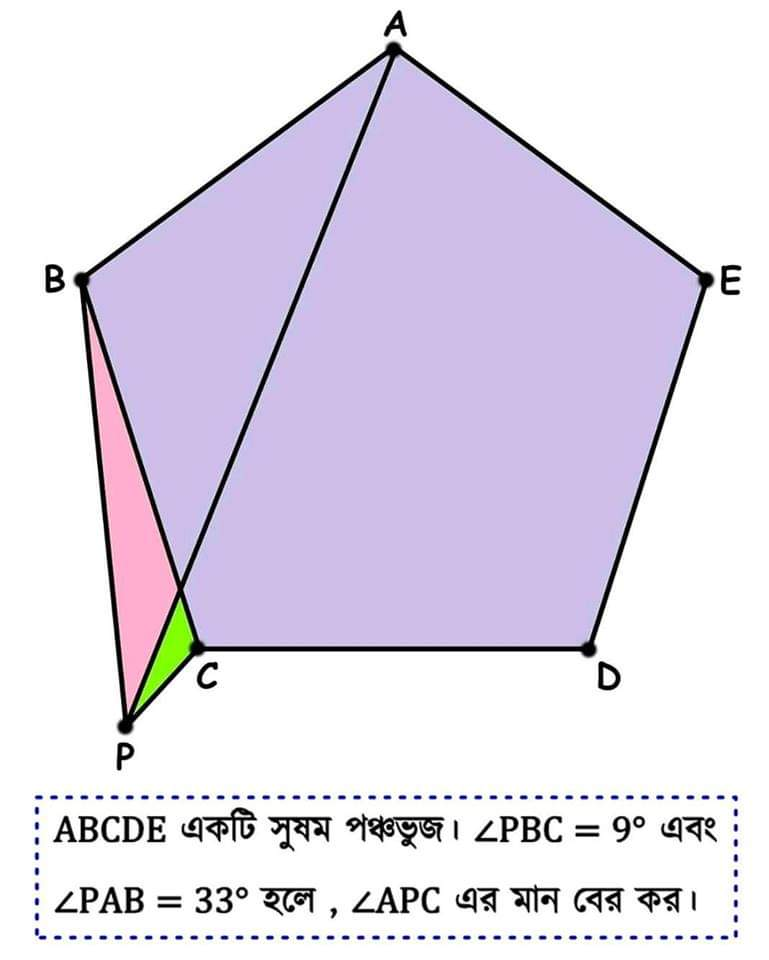
Question Number 58986 Answers: 1 Comments: 3

Question Number 58984 Answers: 1 Comments: 0
Question Number 58979 Answers: 1 Comments: 1
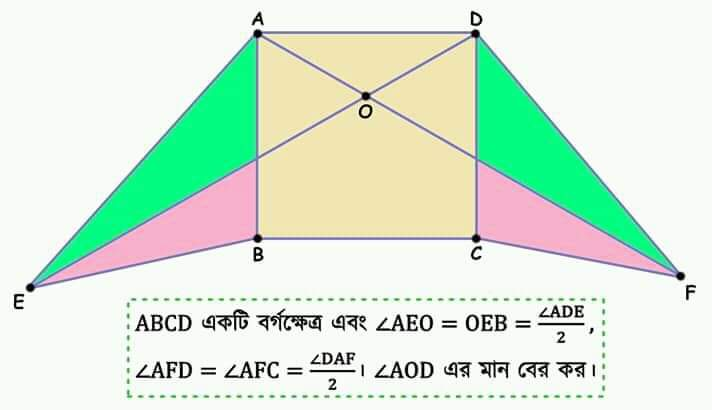
Question Number 58879 Answers: 1 Comments: 0

Question Number 58876 Answers: 1 Comments: 4
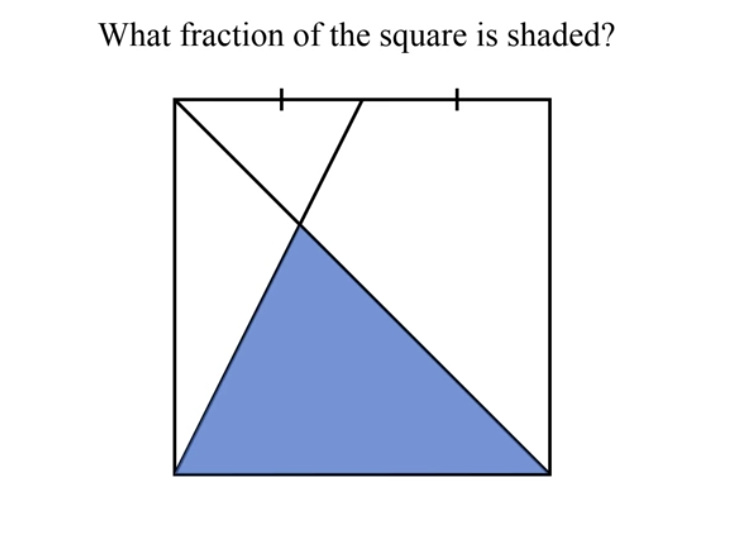
Question Number 58756 Answers: 3 Comments: 0
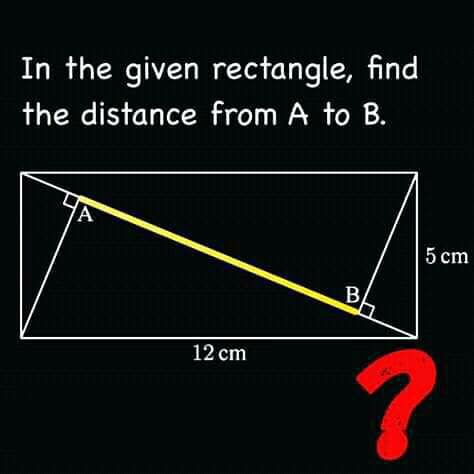
Question Number 58696 Answers: 1 Comments: 3
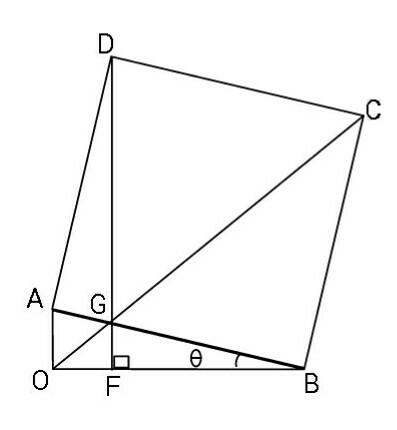
Question Number 58686 Answers: 0 Comments: 1

