
GeometryQuestion and Answers: Page 88
Question Number 64246 Answers: 3 Comments: 0

Question Number 64119 Answers: 3 Comments: 1

Question Number 64097 Answers: 1 Comments: 1
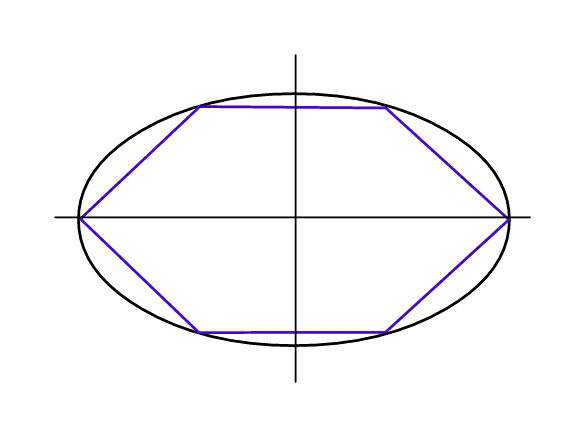
Question Number 64009 Answers: 2 Comments: 1
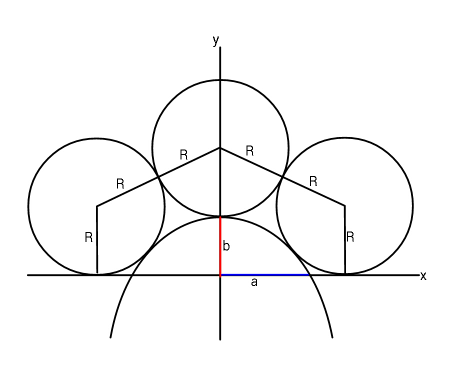
Question Number 63985 Answers: 1 Comments: 0
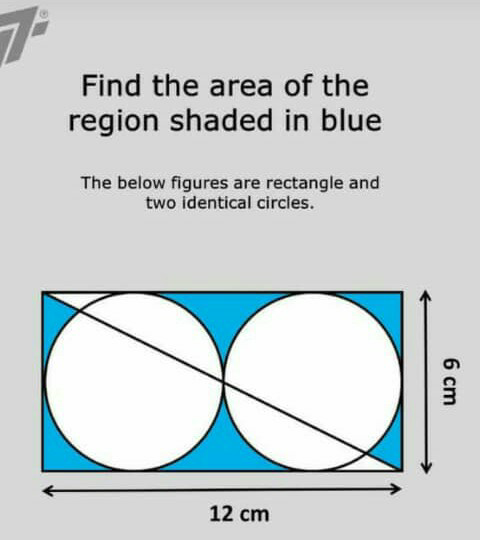
Question Number 63981 Answers: 1 Comments: 0
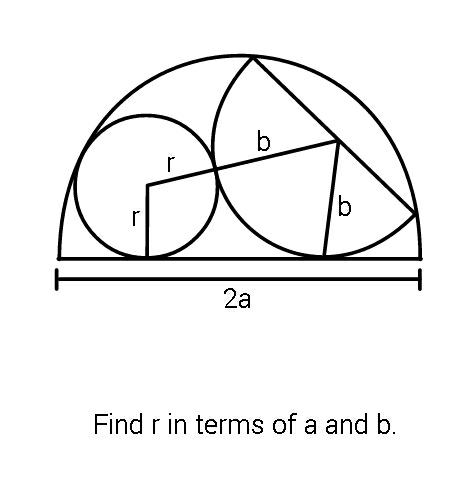
Question Number 63750 Answers: 1 Comments: 2

Question Number 63663 Answers: 1 Comments: 0
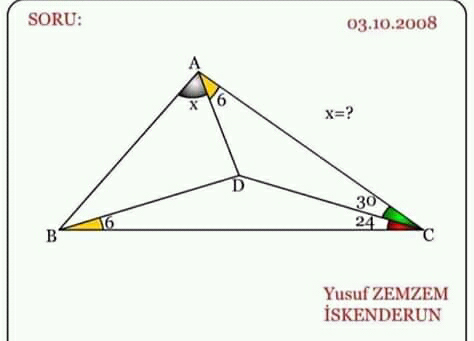
Question Number 63564 Answers: 1 Comments: 0
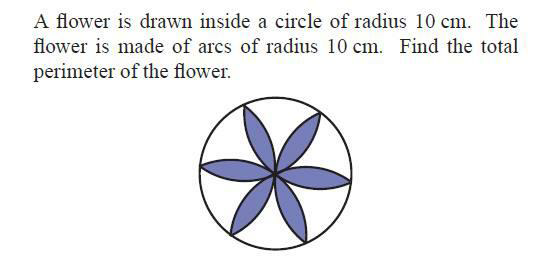
Question Number 63438 Answers: 1 Comments: 2
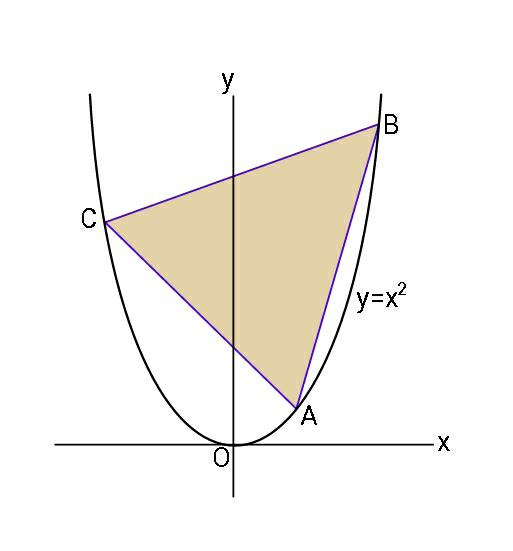
Question Number 63324 Answers: 1 Comments: 0

Question Number 63233 Answers: 0 Comments: 4
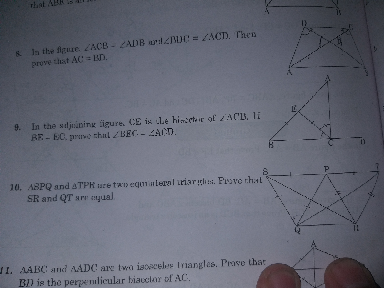
Question Number 63206 Answers: 1 Comments: 1

Question Number 63203 Answers: 0 Comments: 5

Question Number 63194 Answers: 1 Comments: 0
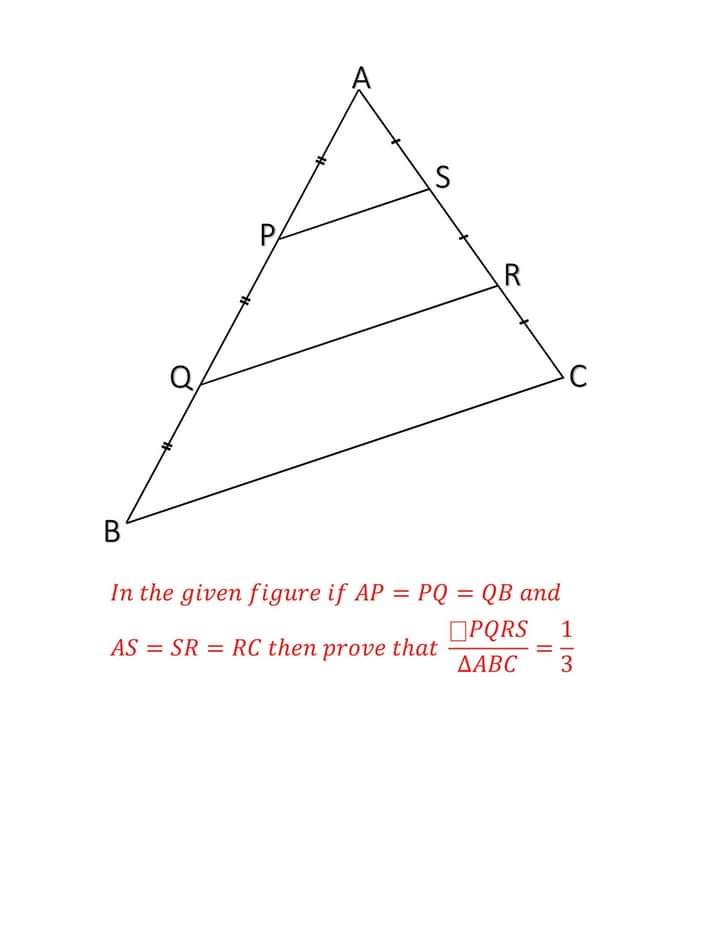
Question Number 63176 Answers: 1 Comments: 1

Question Number 63108 Answers: 2 Comments: 1
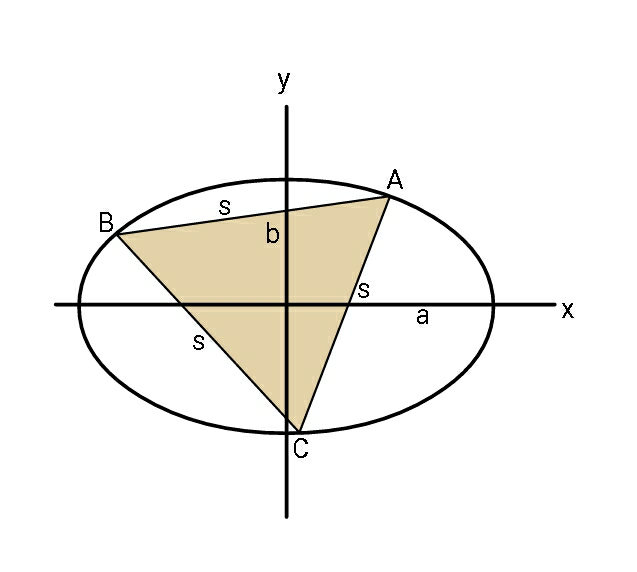
Question Number 62914 Answers: 1 Comments: 0

Question Number 62889 Answers: 1 Comments: 0

Question Number 62850 Answers: 1 Comments: 1
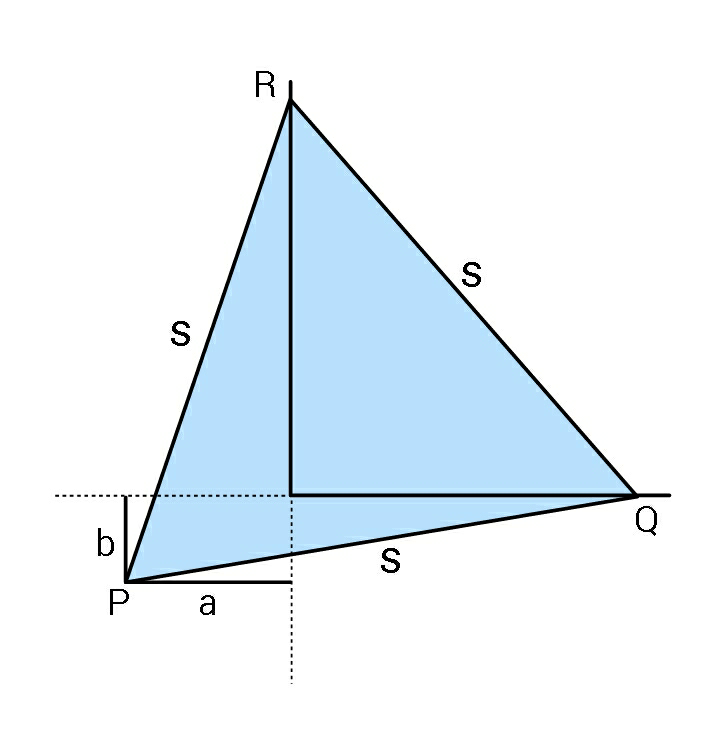
Question Number 62839 Answers: 1 Comments: 3

Question Number 62821 Answers: 2 Comments: 1

Question Number 62735 Answers: 1 Comments: 1

Question Number 62773 Answers: 2 Comments: 1

Question Number 62542 Answers: 1 Comments: 1

Question Number 62523 Answers: 1 Comments: 0

