
GeometryQuestion and Answers: Page 86
Question Number 67692 Answers: 1 Comments: 0

Question Number 67623 Answers: 1 Comments: 5

Question Number 67615 Answers: 2 Comments: 1
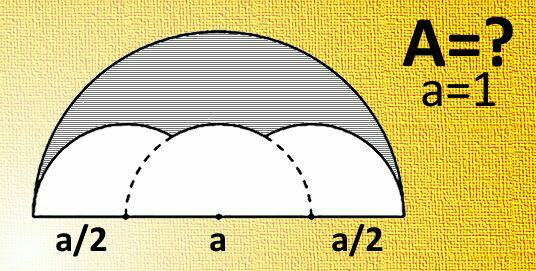
Question Number 67535 Answers: 1 Comments: 5

Question Number 67514 Answers: 1 Comments: 1
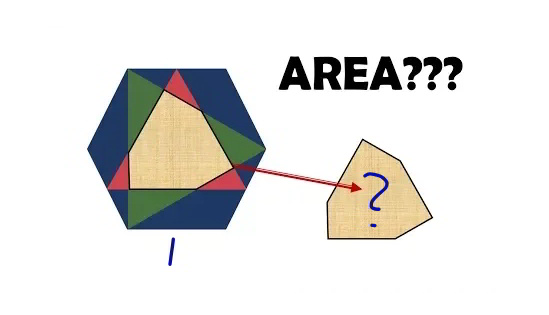
Question Number 67430 Answers: 2 Comments: 2

Question Number 67422 Answers: 1 Comments: 2

Question Number 67386 Answers: 2 Comments: 8

Question Number 67350 Answers: 1 Comments: 1

Question Number 67254 Answers: 1 Comments: 10

Question Number 67116 Answers: 4 Comments: 1

Question Number 67102 Answers: 2 Comments: 0
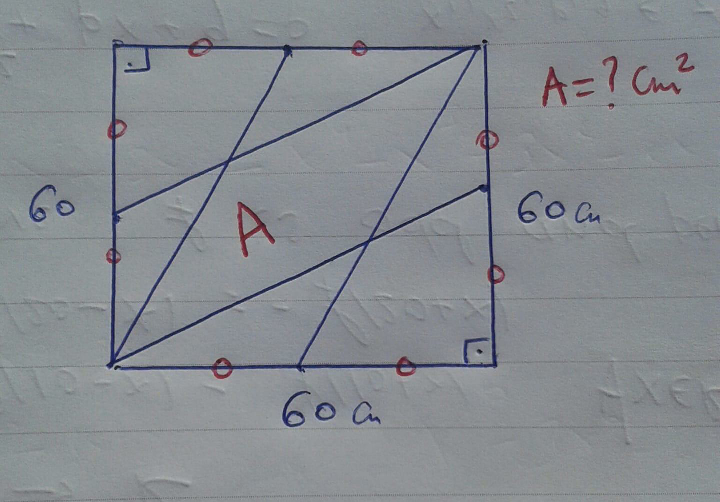
Question Number 67072 Answers: 1 Comments: 0

Question Number 67071 Answers: 0 Comments: 7

Question Number 67033 Answers: 0 Comments: 5

Question Number 67026 Answers: 0 Comments: 5
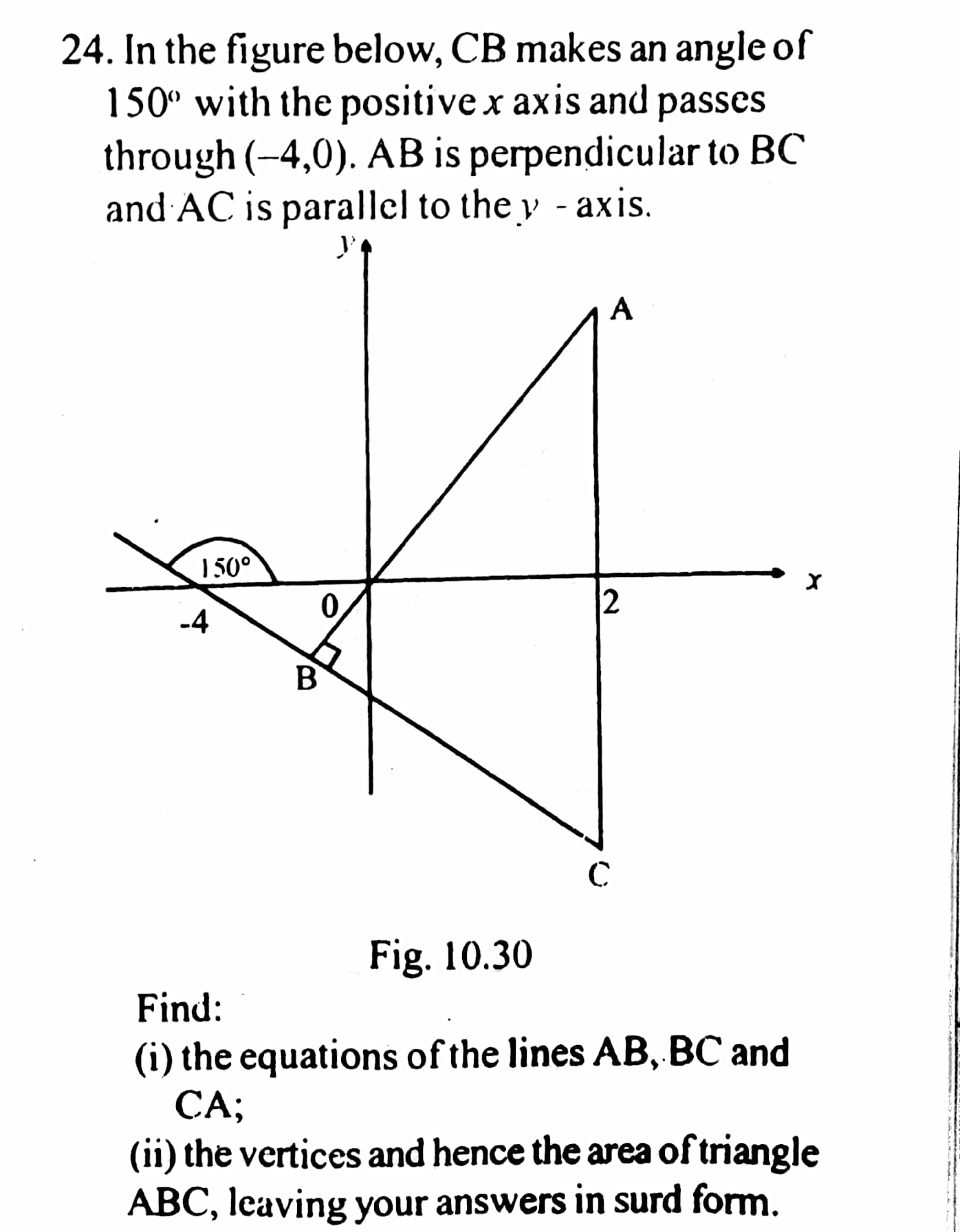
Question Number 66656 Answers: 1 Comments: 1

Question Number 66527 Answers: 1 Comments: 1

Question Number 66522 Answers: 3 Comments: 0

Question Number 66469 Answers: 0 Comments: 1

Question Number 66310 Answers: 1 Comments: 1
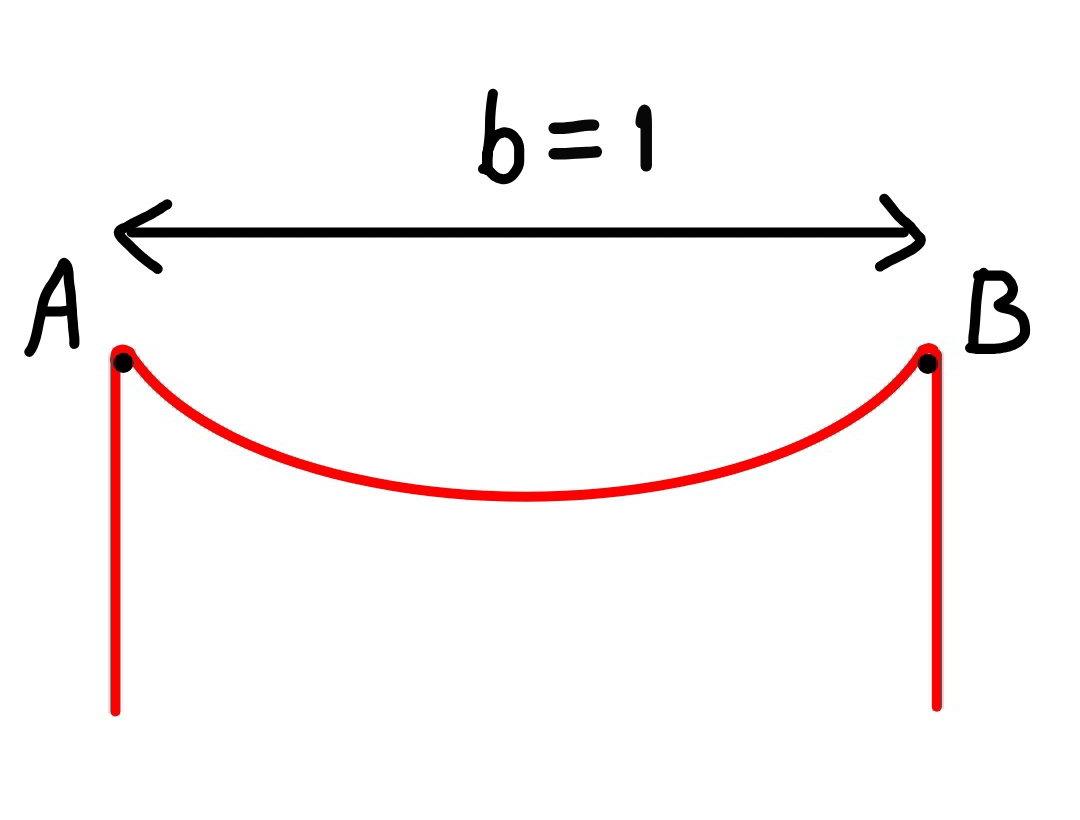
Question Number 66211 Answers: 1 Comments: 4

Question Number 66109 Answers: 1 Comments: 1
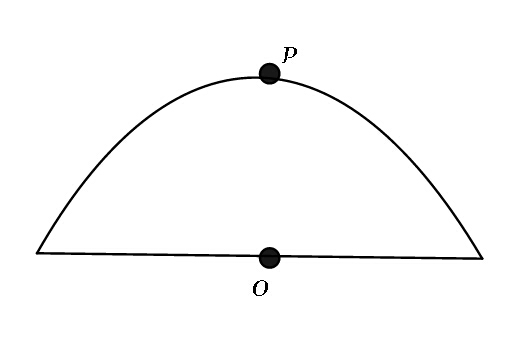
Question Number 65980 Answers: 3 Comments: 1
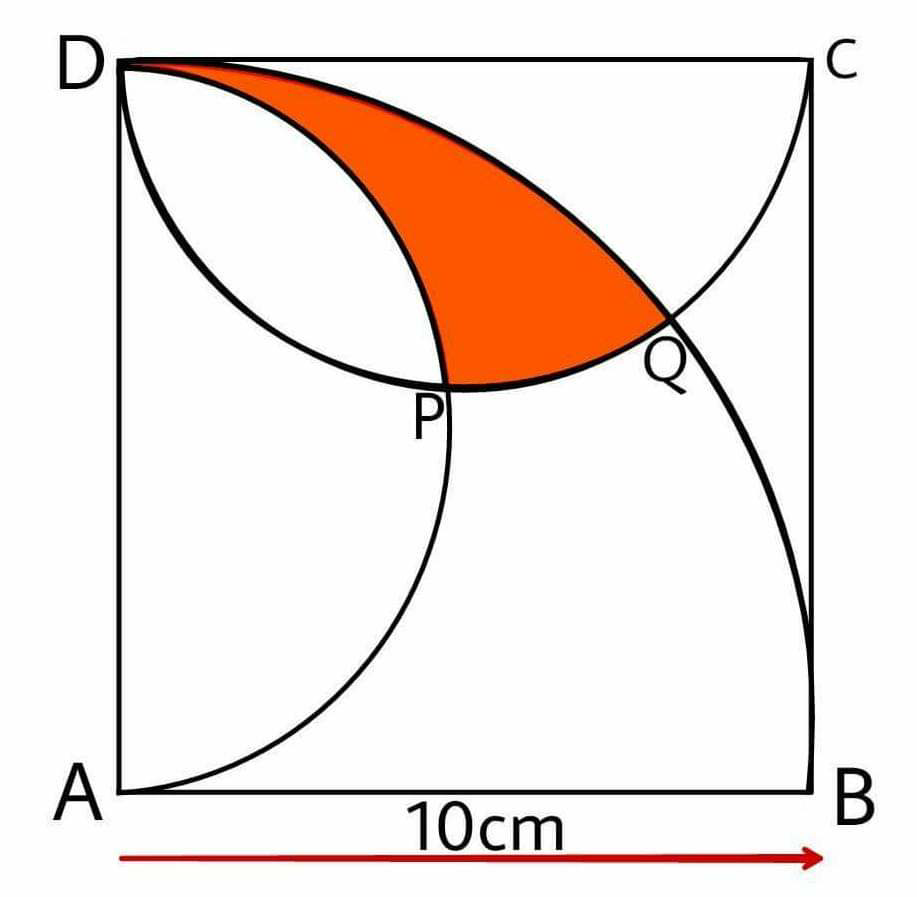
Question Number 65884 Answers: 0 Comments: 3

Question Number 65541 Answers: 0 Comments: 0
