
GeometryQuestion and Answers: Page 78
Question Number 82302 Answers: 0 Comments: 2

Question Number 82273 Answers: 0 Comments: 2

Question Number 82131 Answers: 2 Comments: 4

Question Number 82088 Answers: 0 Comments: 0
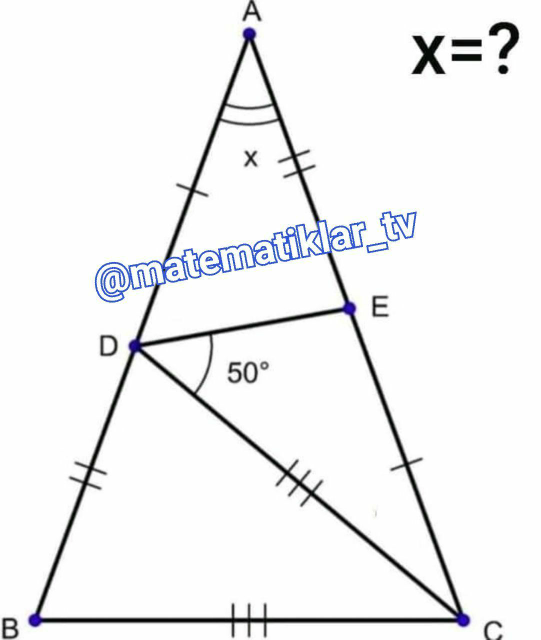
Question Number 82042 Answers: 0 Comments: 4

Question Number 81972 Answers: 1 Comments: 1

Question Number 81887 Answers: 0 Comments: 2

Question Number 81755 Answers: 1 Comments: 0

Question Number 81649 Answers: 0 Comments: 6
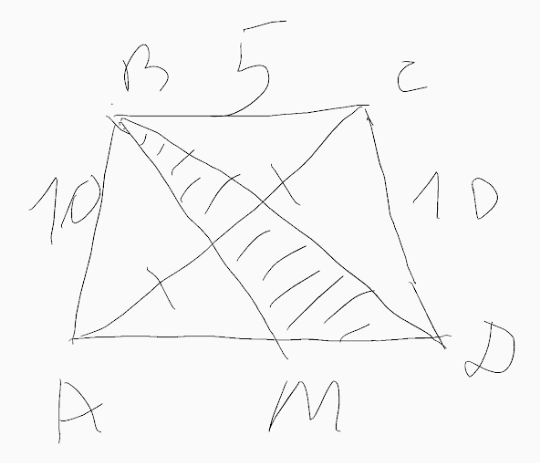
Question Number 81610 Answers: 1 Comments: 0

Question Number 81467 Answers: 1 Comments: 1

Question Number 81331 Answers: 0 Comments: 10

Question Number 81322 Answers: 1 Comments: 1

Question Number 81303 Answers: 1 Comments: 1

Question Number 81289 Answers: 0 Comments: 5
$${discussthesymmetryofthefollowingcurves} \\ $$$${squareofx}+{squareofy}=\mathrm{1} \\ $$
Question Number 81193 Answers: 1 Comments: 3

Question Number 81122 Answers: 1 Comments: 4

Question Number 81075 Answers: 2 Comments: 1
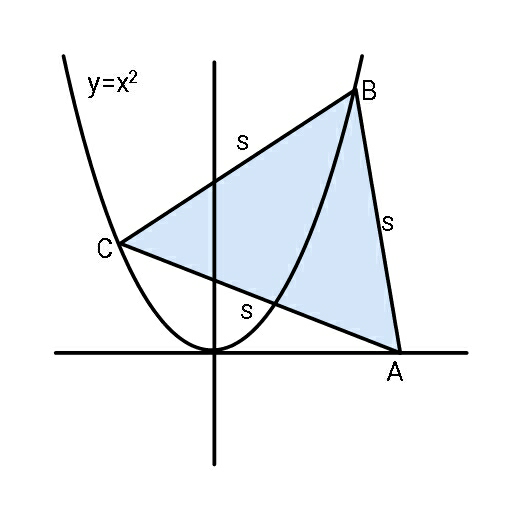
Question Number 80809 Answers: 1 Comments: 5
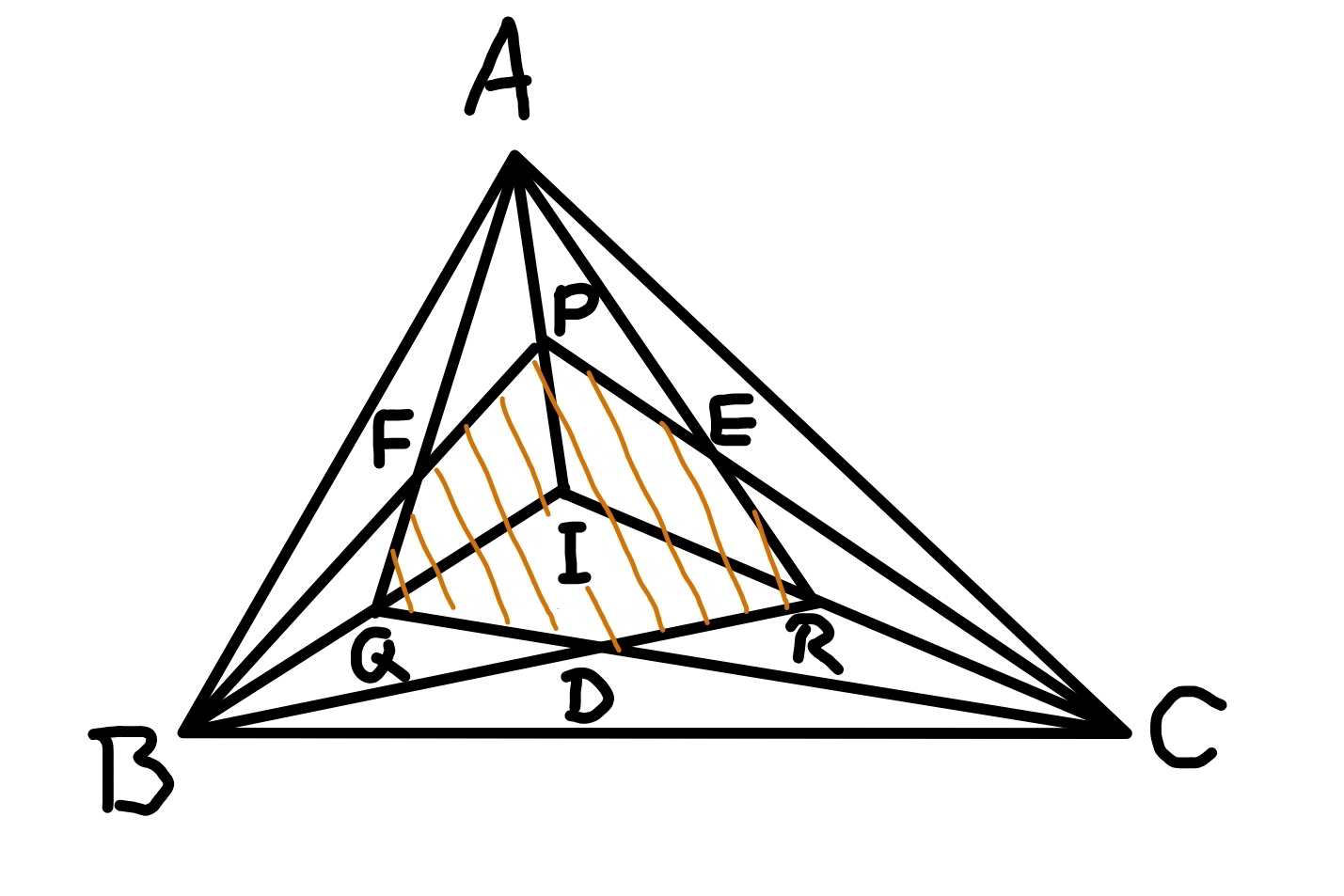
Question Number 80795 Answers: 0 Comments: 3

Question Number 80761 Answers: 0 Comments: 1

Question Number 80731 Answers: 1 Comments: 1

Question Number 80682 Answers: 0 Comments: 3

Question Number 80587 Answers: 1 Comments: 6

Question Number 80574 Answers: 1 Comments: 2

Question Number 80539 Answers: 0 Comments: 1

