
GeometryQuestion and Answers: Page 75
Question Number 80809 Answers: 1 Comments: 5
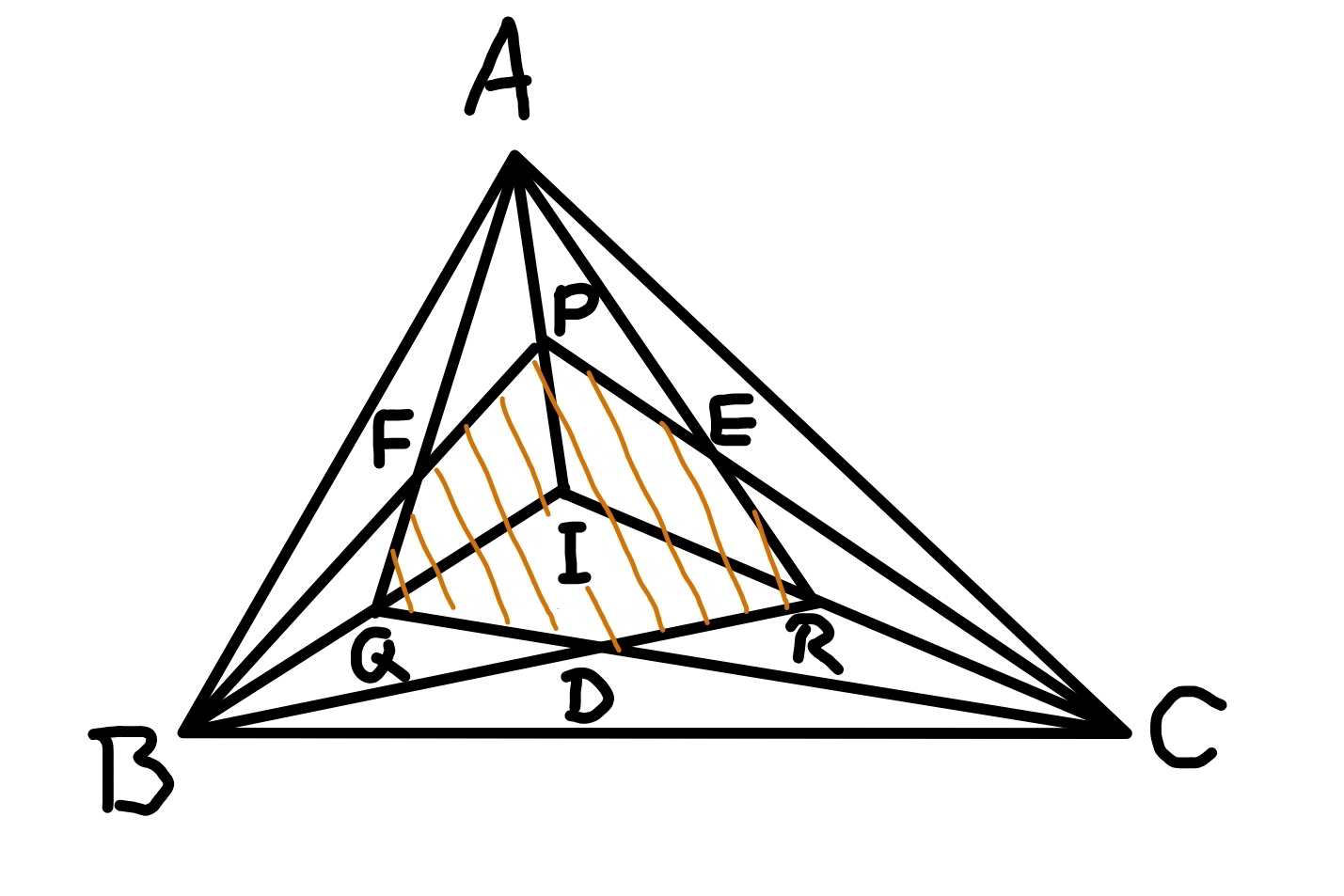
Question Number 80795 Answers: 0 Comments: 3

Question Number 80761 Answers: 0 Comments: 1

Question Number 80731 Answers: 1 Comments: 1

Question Number 80682 Answers: 0 Comments: 3

Question Number 80587 Answers: 1 Comments: 6

Question Number 80574 Answers: 1 Comments: 2

Question Number 80539 Answers: 0 Comments: 1

Question Number 80477 Answers: 0 Comments: 5

Question Number 80260 Answers: 0 Comments: 3

Question Number 80222 Answers: 1 Comments: 2

Question Number 80015 Answers: 2 Comments: 2
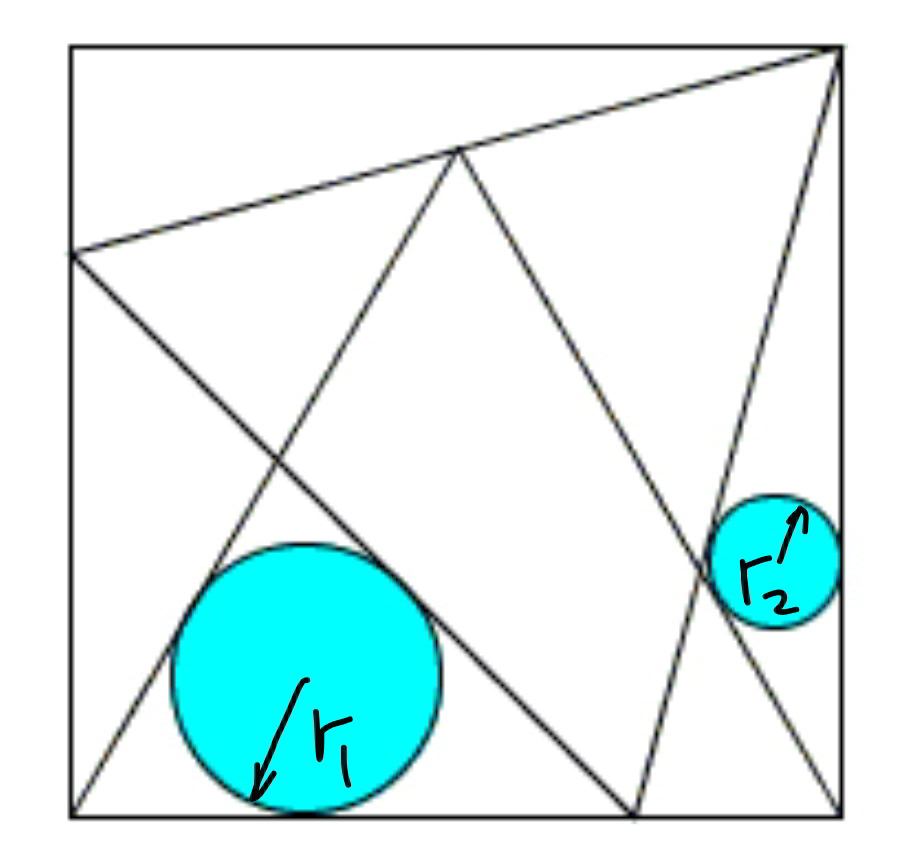
Question Number 79798 Answers: 0 Comments: 7
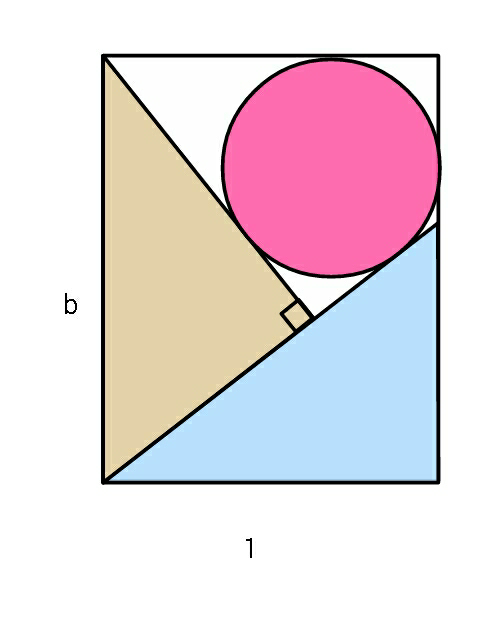
Question Number 79794 Answers: 1 Comments: 2

Question Number 79694 Answers: 0 Comments: 1

Question Number 79675 Answers: 0 Comments: 11

Question Number 79649 Answers: 1 Comments: 6
Question Number 79609 Answers: 1 Comments: 1

Question Number 79572 Answers: 1 Comments: 1
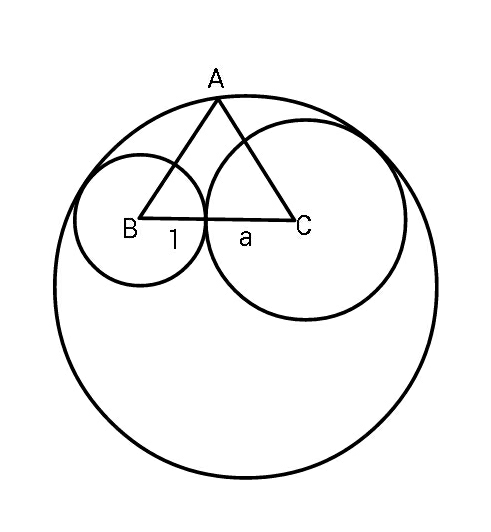
Question Number 79449 Answers: 1 Comments: 6
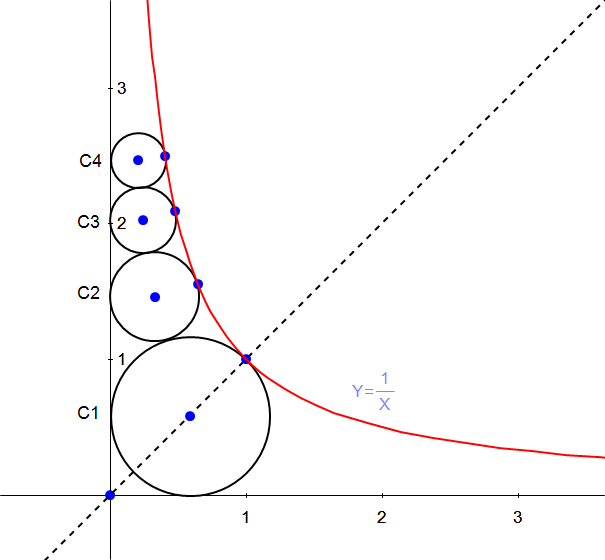
Question Number 79377 Answers: 1 Comments: 3
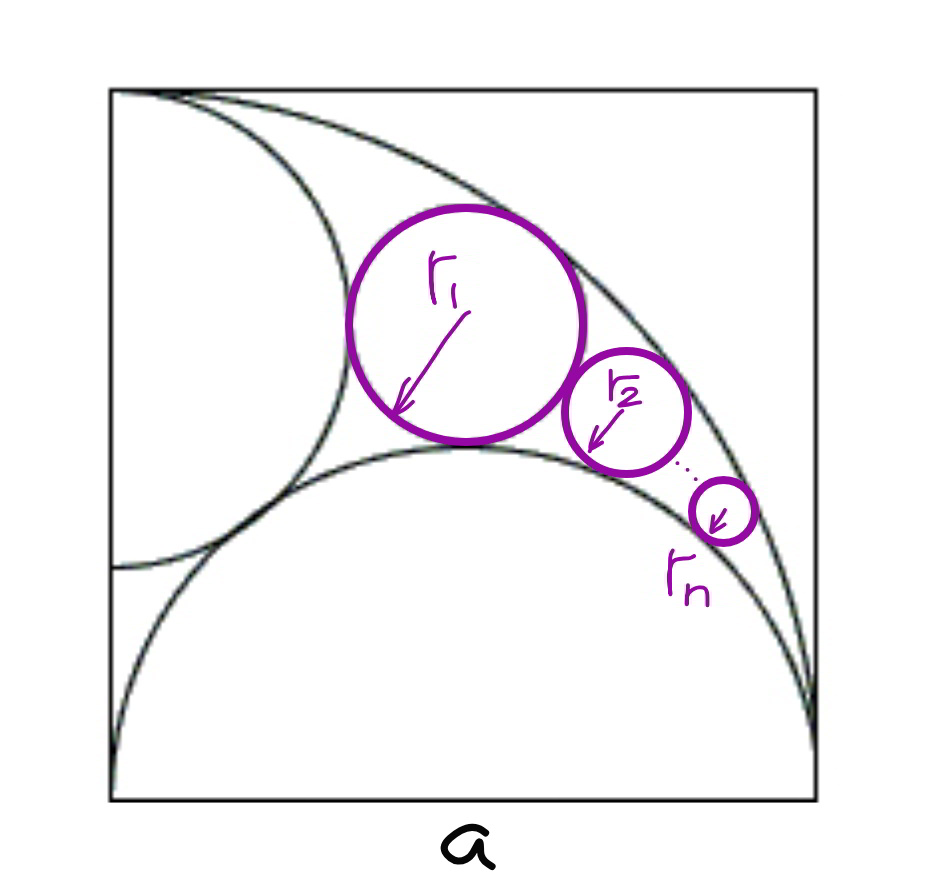
Question Number 79368 Answers: 2 Comments: 6

Question Number 79365 Answers: 1 Comments: 1
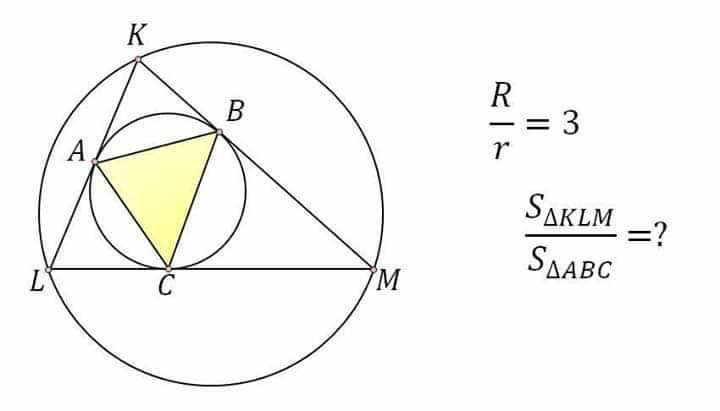
Question Number 79361 Answers: 1 Comments: 1
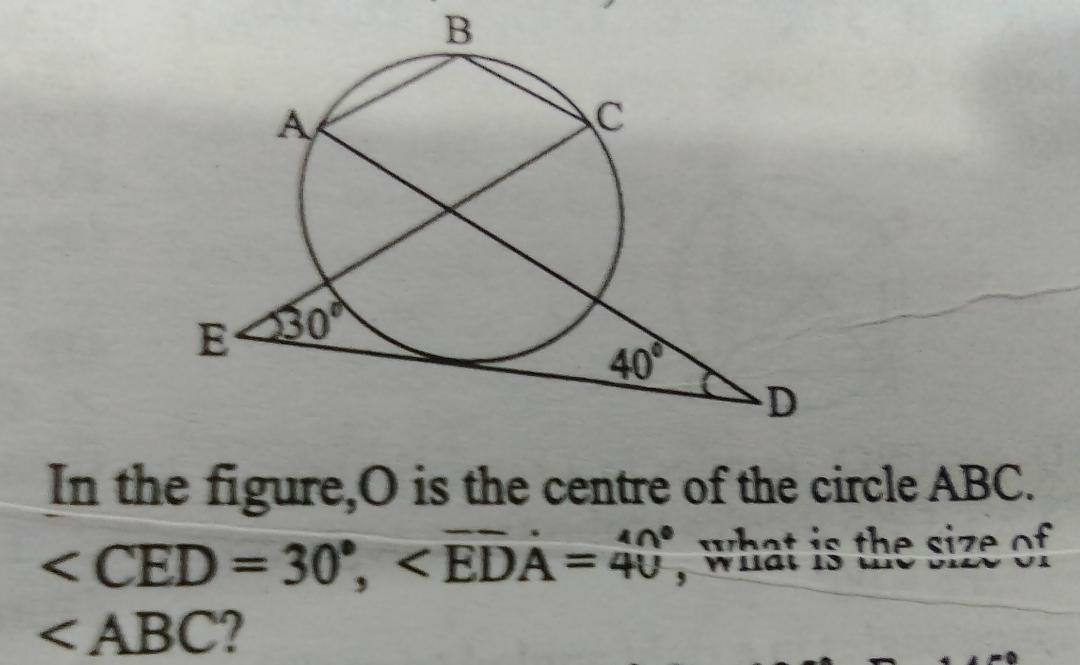
Question Number 79309 Answers: 1 Comments: 3
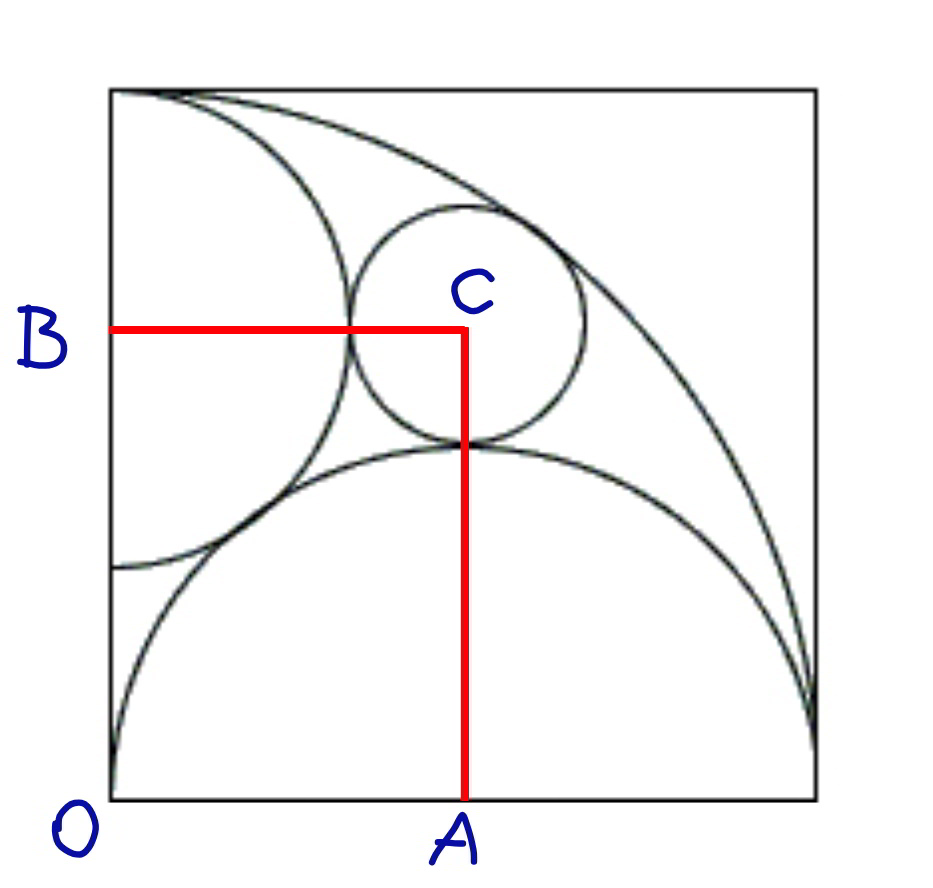
Question Number 79254 Answers: 4 Comments: 2

