Question and Answers Forum

All Questions Topic List

GeometryQuestion and Answers: Page 74

Question Number 90356 Answers: 0 Comments: 0

Question Number 90347 Answers: 2 Comments: 5

Question Number 90330 Answers: 0 Comments: 1

Question Number 90272 Answers: 1 Comments: 0

Question Number 90157 Answers: 0 Comments: 0

Question Number 90161 Answers: 1 Comments: 0

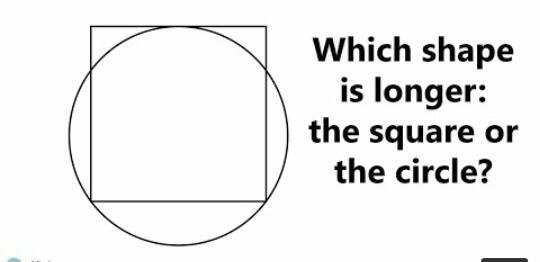
Question Number 90069 Answers: 2 Comments: 3

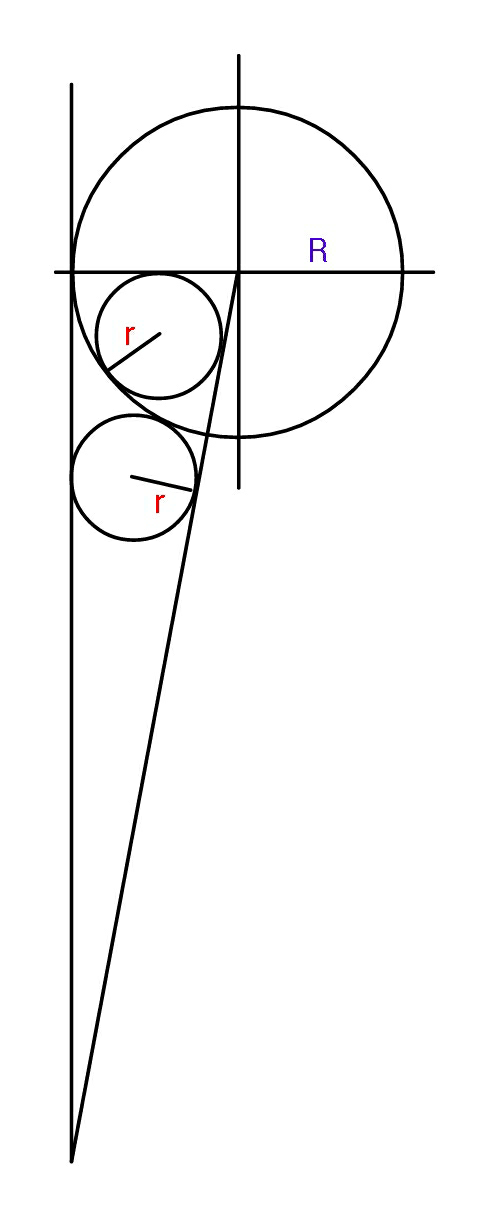
Question Number 90058 Answers: 1 Comments: 1

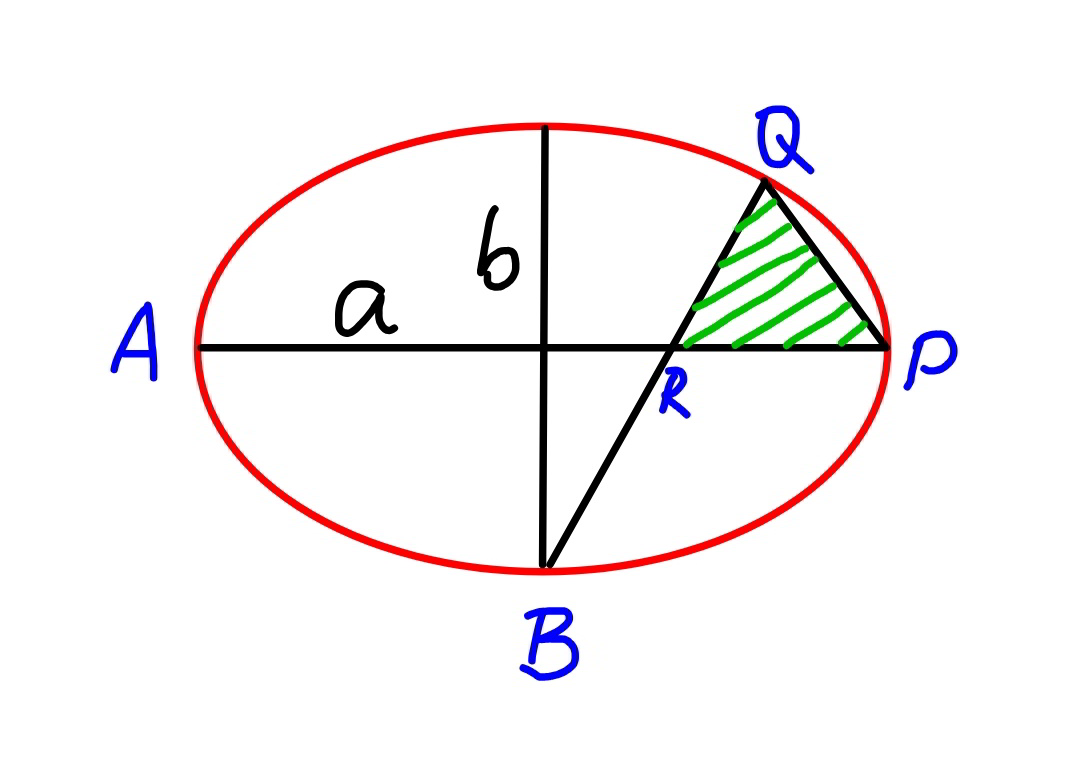
Question Number 90011 Answers: 0 Comments: 6

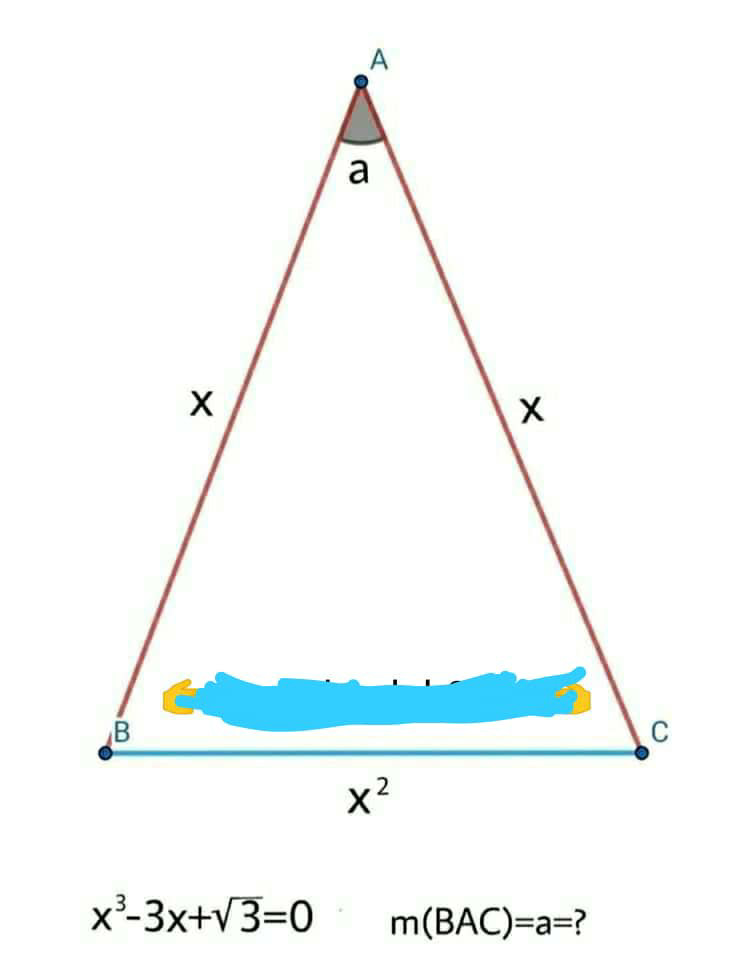
Question Number 89950 Answers: 0 Comments: 1

Question Number 89849 Answers: 3 Comments: 1

Question Number 89781 Answers: 0 Comments: 8

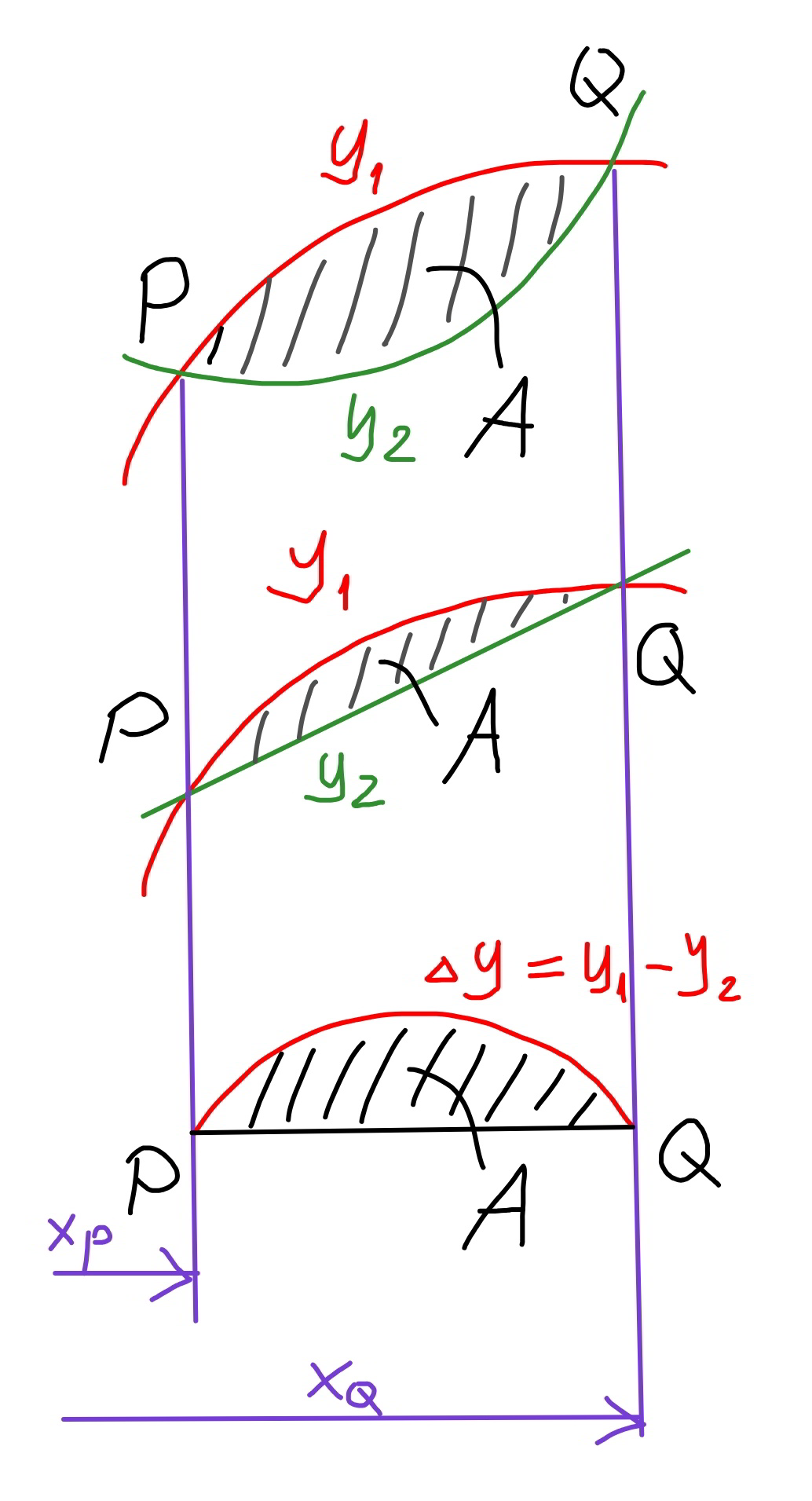
Question Number 89618 Answers: 1 Comments: 2

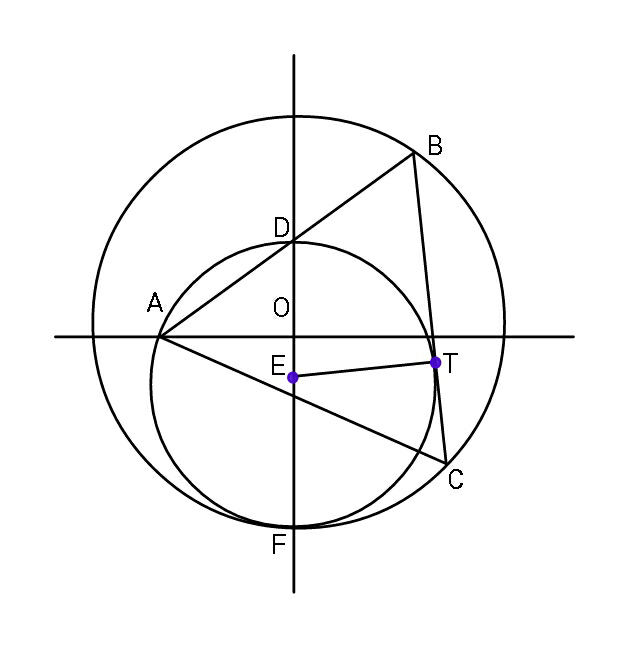
Question Number 89496 Answers: 2 Comments: 0

Question Number 89412 Answers: 0 Comments: 8

Question Number 89361 Answers: 1 Comments: 0

Question Number 89290 Answers: 1 Comments: 2

Question Number 89097 Answers: 1 Comments: 1

Question Number 88933 Answers: 0 Comments: 5

Question Number 88894 Answers: 0 Comments: 1

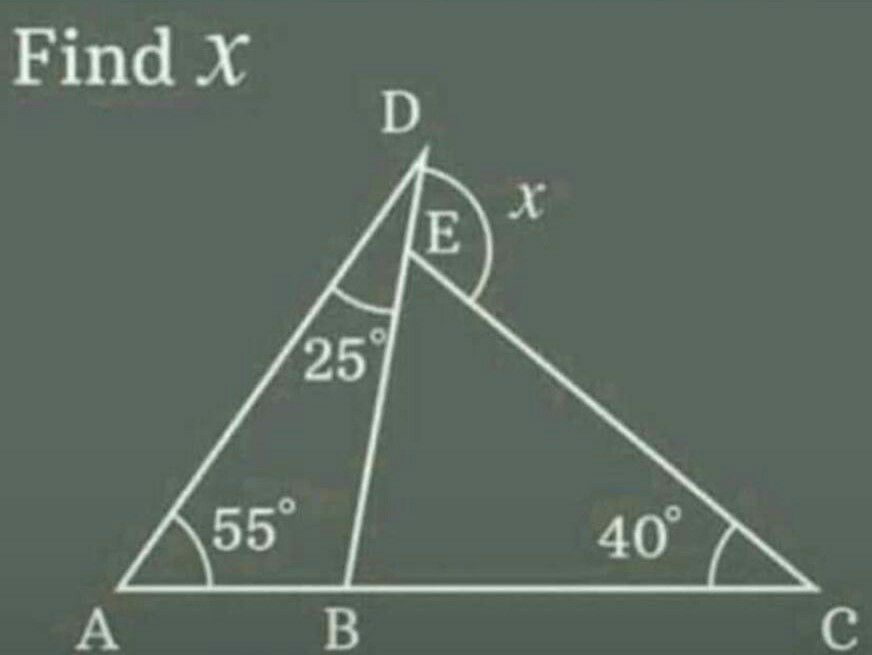
Question Number 88886 Answers: 1 Comments: 5

Question Number 88865 Answers: 0 Comments: 1

Question Number 88758 Answers: 2 Comments: 22

Some people may have noticed that i usually calculate areas concerning parabola directly, without applying complicated integral calculus. Here i am giving you the backgroud. Actually you know all these things and you are able to prove them. Maybe you just forget to apply them.

$${Some}\:{people}\:{may}\:{have}\:{noticed}\:{that}\:{i} \\ $$$${usually}\:{calculate}\:{areas}\:{concerning} \\ $$$${parabola}\:{directly},\:{without}\:{applying} \\ $$$${complicated}\:{integral}\:{calculus}. \\ $$$${Here}\:{i}\:{am}\:{giving}\:{you}\:{the}\:{backgroud}.\: \\ $$$${Actually}\:{you}\:{know}\:{all}\:{these}\:{things}\:{and} \\ $$$${you}\:{are}\:{able}\:{to}\:{prove}\:{them}.\:{Maybe} \\ $$$${you}\:{just}\:{forget}\:{to}\:{apply}\:{them}. \\ $$

Question Number 88754 Answers: 1 Comments: 3

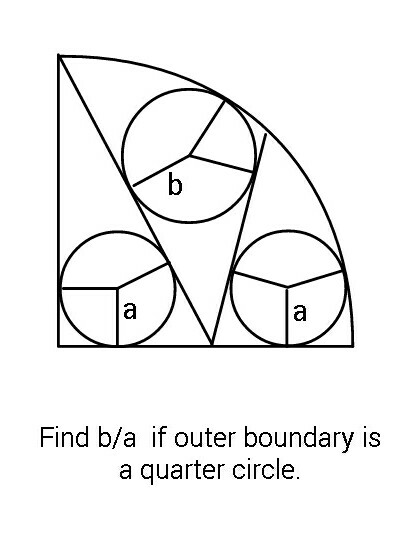
Question Number 88731 Answers: 0 Comments: 3

Question Number 88708 Answers: 2 Comments: 5

Pg 69 Pg 70 Pg 71 Pg 72 Pg 73 Pg 74 Pg 75 Pg 76 Pg 77 Pg 78

Terms of Service

Contact: info@tinkutara.com