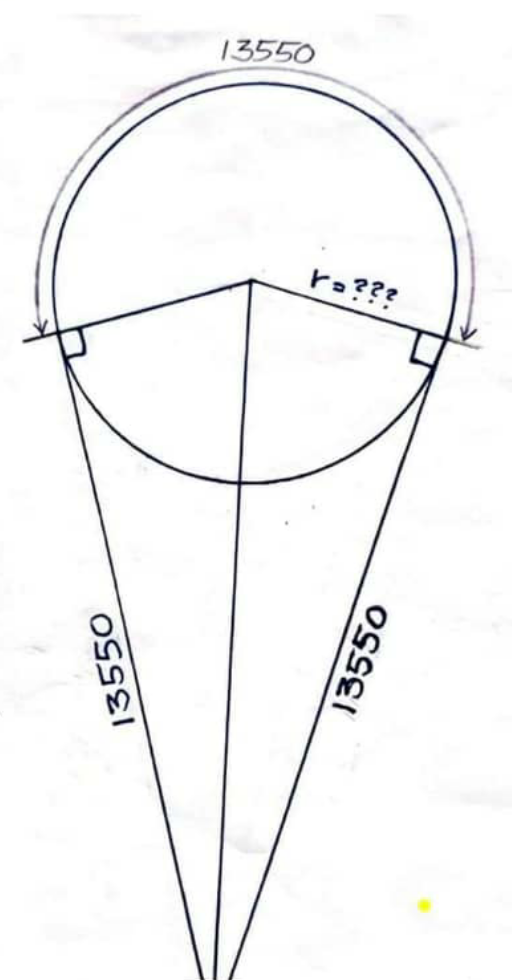
GeometryQuestion and Answers: Page 66
Question Number 128145 Answers: 0 Comments: 6

Question Number 127879 Answers: 0 Comments: 0

Question Number 127740 Answers: 1 Comments: 5

Question Number 127749 Answers: 1 Comments: 1

Question Number 127654 Answers: 1 Comments: 0

Question Number 127583 Answers: 0 Comments: 0

Question Number 127337 Answers: 0 Comments: 2
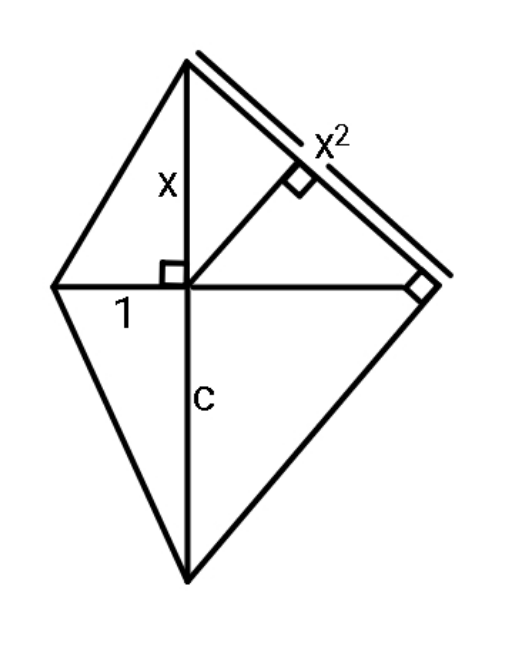
Question Number 127018 Answers: 1 Comments: 0
Question Number 126609 Answers: 1 Comments: 0
Question Number 126557 Answers: 0 Comments: 3
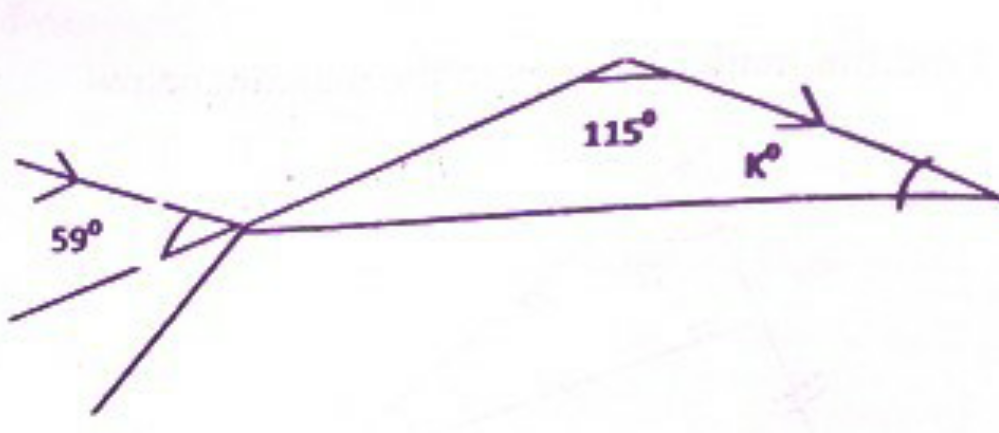
Question Number 126509 Answers: 1 Comments: 0
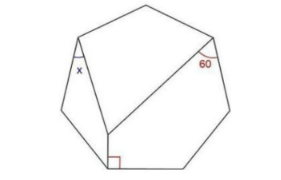
Question Number 126080 Answers: 1 Comments: 3
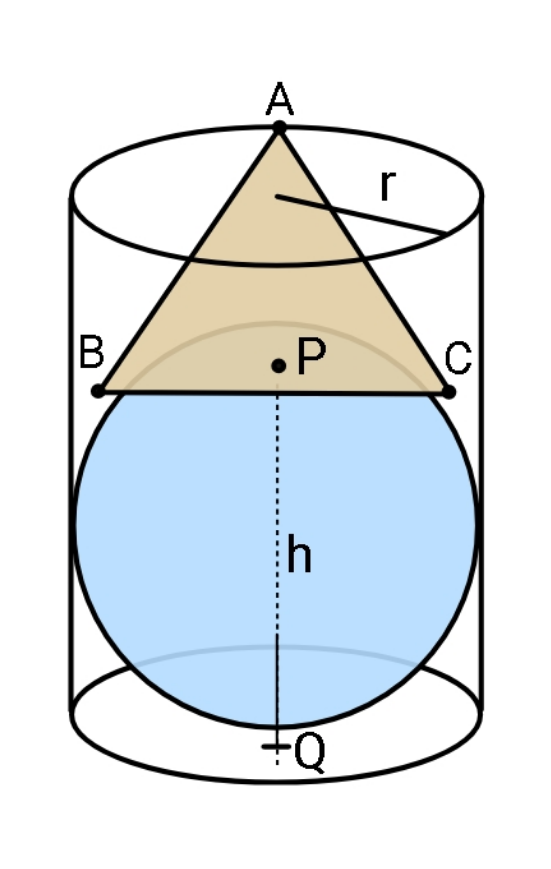
Question Number 126052 Answers: 0 Comments: 0
Question Number 126049 Answers: 0 Comments: 0
Question Number 125907 Answers: 2 Comments: 1
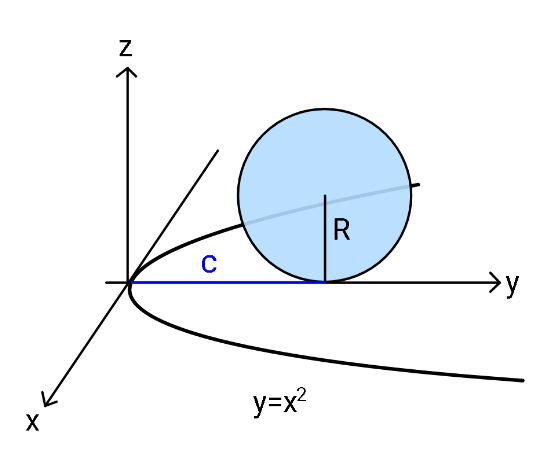
Question Number 125800 Answers: 3 Comments: 5

Question Number 125508 Answers: 3 Comments: 1

Question Number 125456 Answers: 0 Comments: 1
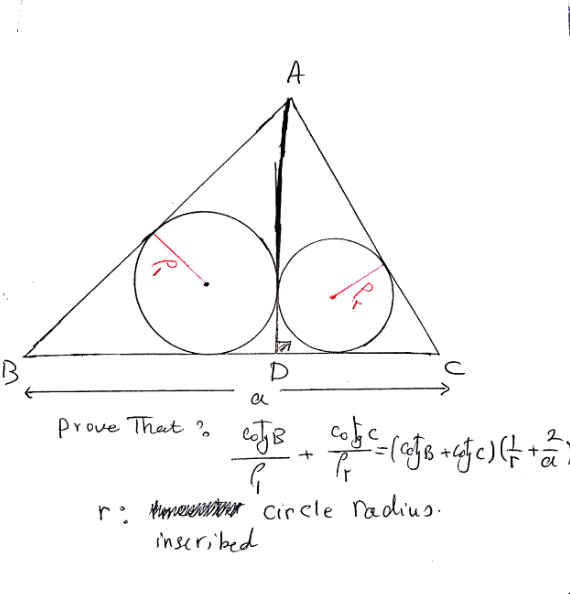
Question Number 125384 Answers: 1 Comments: 1
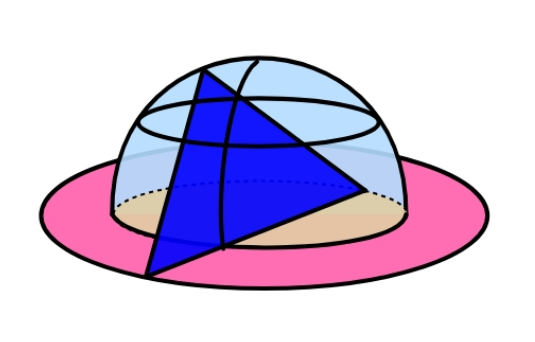
Question Number 125090 Answers: 0 Comments: 8

Question Number 125070 Answers: 0 Comments: 3
Question Number 125016 Answers: 0 Comments: 0
Question Number 124953 Answers: 1 Comments: 0

Question Number 124928 Answers: 1 Comments: 0
Question Number 124869 Answers: 0 Comments: 0

Question Number 124722 Answers: 1 Comments: 0