
GeometryQuestion and Answers: Page 48
Question Number 176531 Answers: 1 Comments: 4
Question Number 176437 Answers: 1 Comments: 0
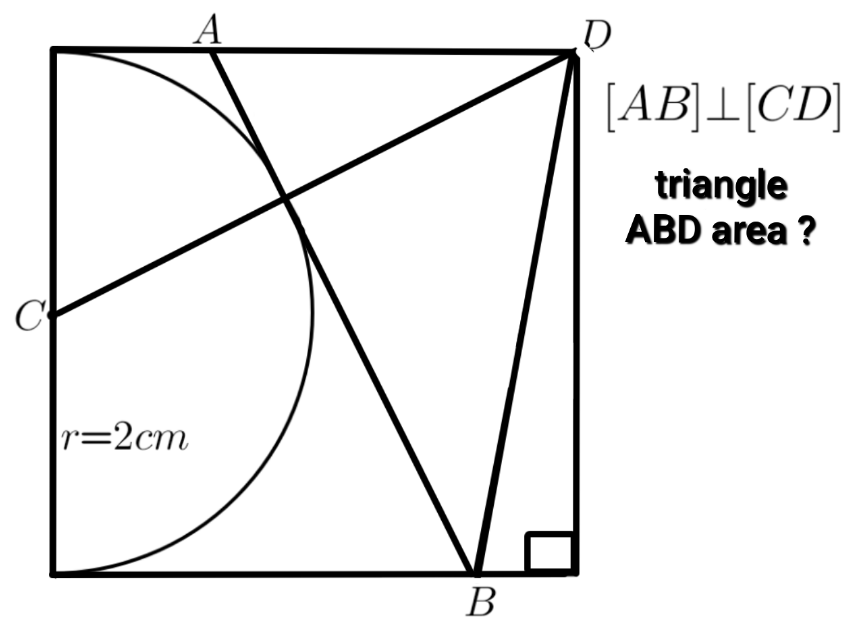
Question Number 176367 Answers: 1 Comments: 1

Question Number 176776 Answers: 2 Comments: 0

Question Number 176195 Answers: 1 Comments: 0
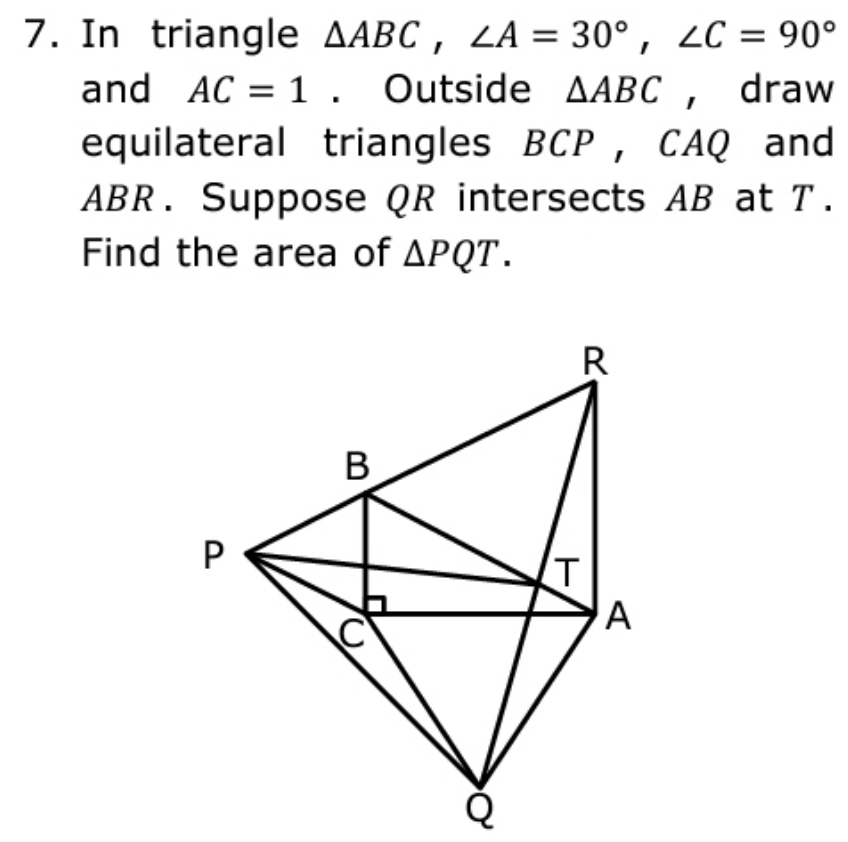
Question Number 176192 Answers: 1 Comments: 0
Question Number 176100 Answers: 2 Comments: 0
Question Number 176086 Answers: 0 Comments: 1
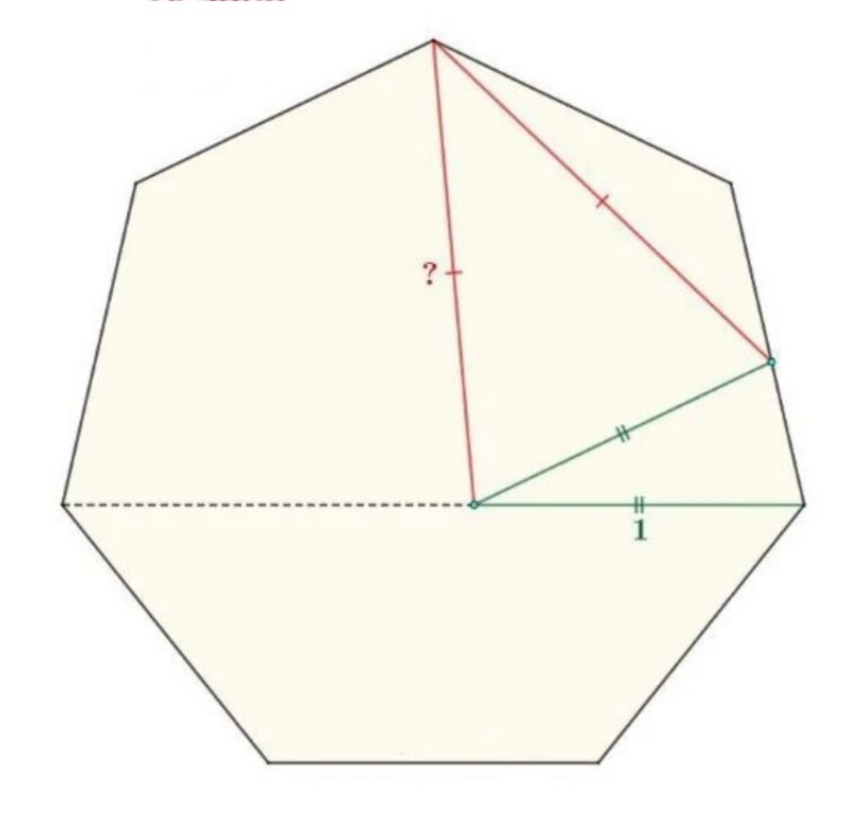
Question Number 176076 Answers: 0 Comments: 1

Question Number 176014 Answers: 3 Comments: 1

Question Number 175717 Answers: 1 Comments: 0

Question Number 175601 Answers: 2 Comments: 0

Question Number 175568 Answers: 1 Comments: 1

Question Number 175511 Answers: 0 Comments: 1
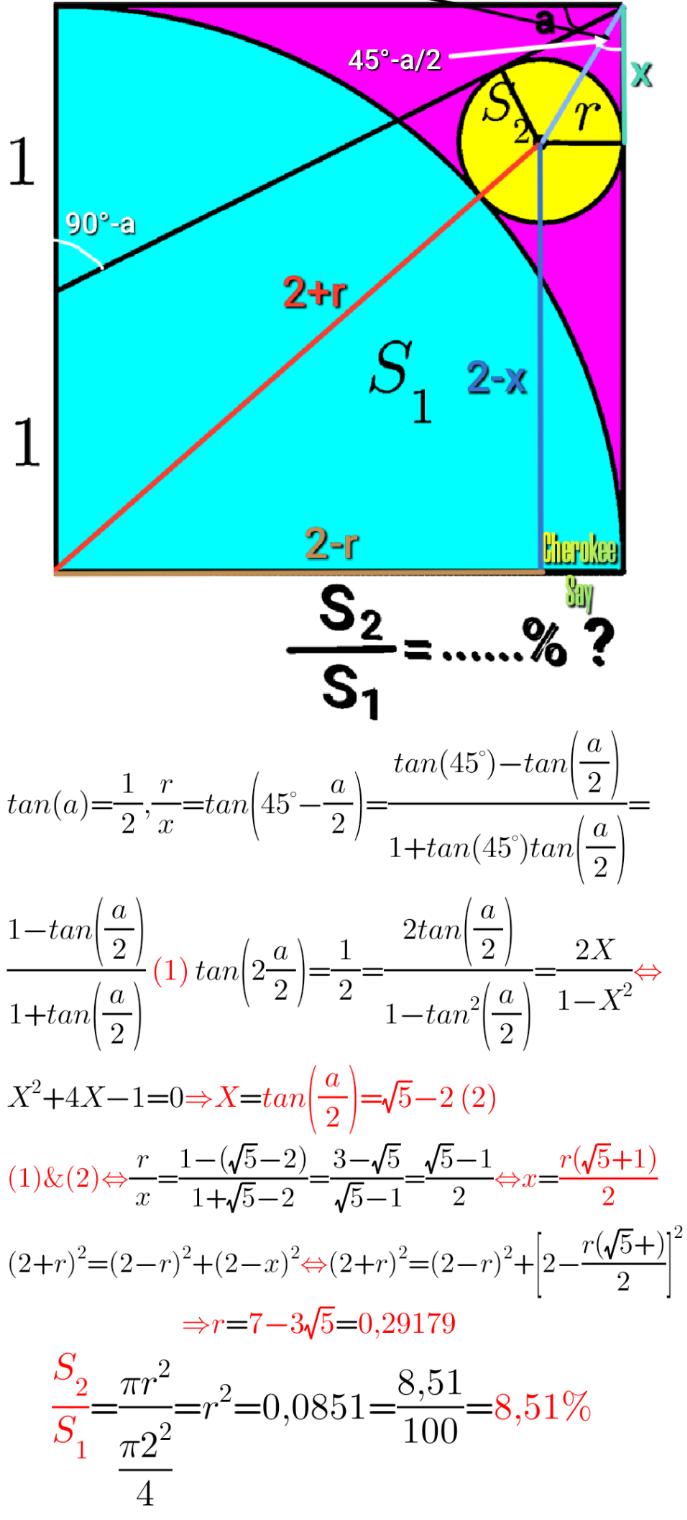
Question Number 175476 Answers: 1 Comments: 1

Question Number 175449 Answers: 1 Comments: 1

Question Number 181496 Answers: 1 Comments: 0
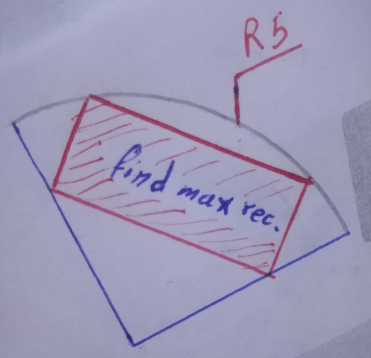
Question Number 181494 Answers: 0 Comments: 0
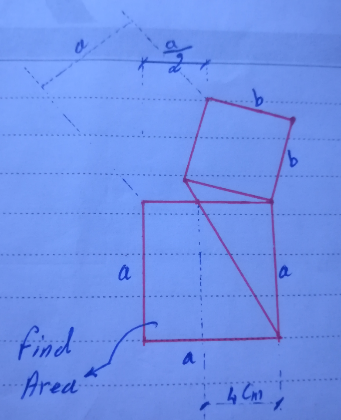
Question Number 181485 Answers: 2 Comments: 0
Question Number 175199 Answers: 1 Comments: 0
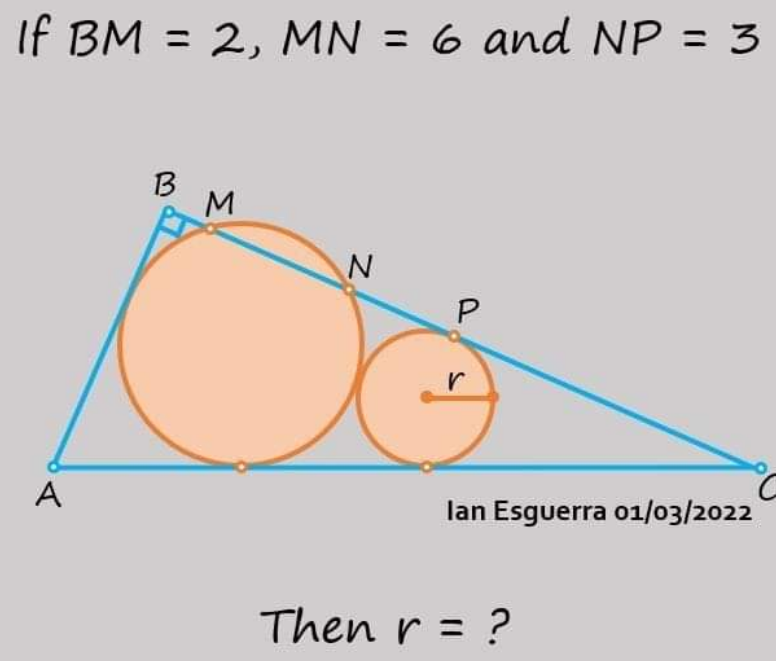
Question Number 175188 Answers: 1 Comments: 0
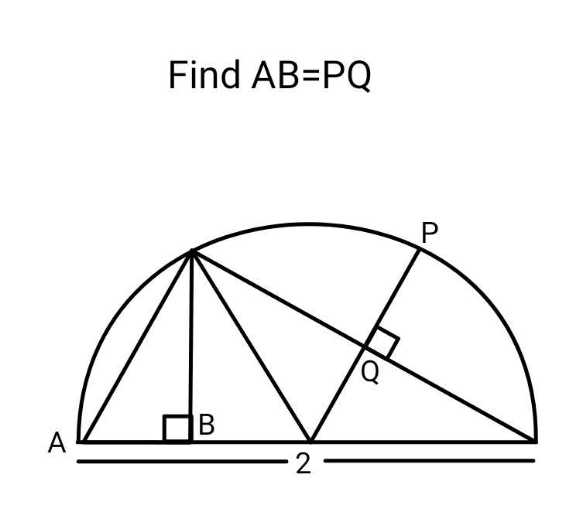
Question Number 175176 Answers: 2 Comments: 0
Question Number 175172 Answers: 0 Comments: 0

Question Number 175166 Answers: 1 Comments: 0

Question Number 175149 Answers: 1 Comments: 0

Question Number 175045 Answers: 0 Comments: 5
