GeometryQuestion and Answers: Page 45
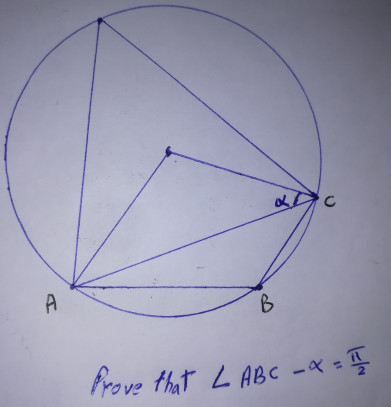
Question Number 181151 Answers: 4 Comments: 0

Question Number 181128 Answers: 0 Comments: 2

Question Number 181125 Answers: 1 Comments: 3
Question Number 181085 Answers: 1 Comments: 3

Question Number 181070 Answers: 2 Comments: 2

Question Number 181055 Answers: 2 Comments: 14

Question Number 181051 Answers: 1 Comments: 0
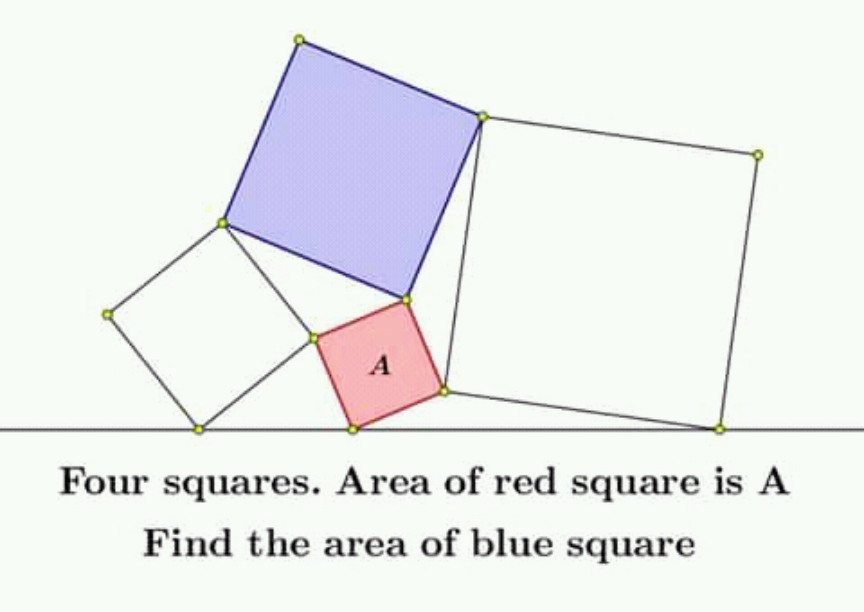
Question Number 181019 Answers: 1 Comments: 0

Question Number 180998 Answers: 2 Comments: 0
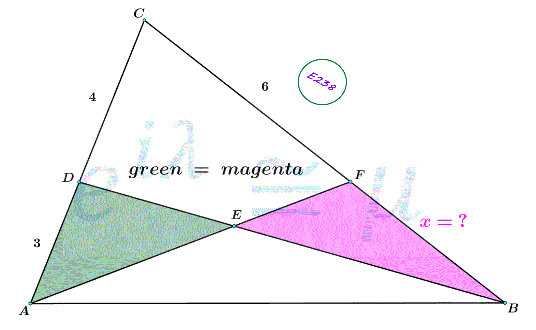
Question Number 180939 Answers: 0 Comments: 2

Question Number 180931 Answers: 0 Comments: 2

Question Number 180927 Answers: 2 Comments: 1

Question Number 180882 Answers: 1 Comments: 1

Question Number 180897 Answers: 1 Comments: 5

Question Number 180813 Answers: 1 Comments: 5
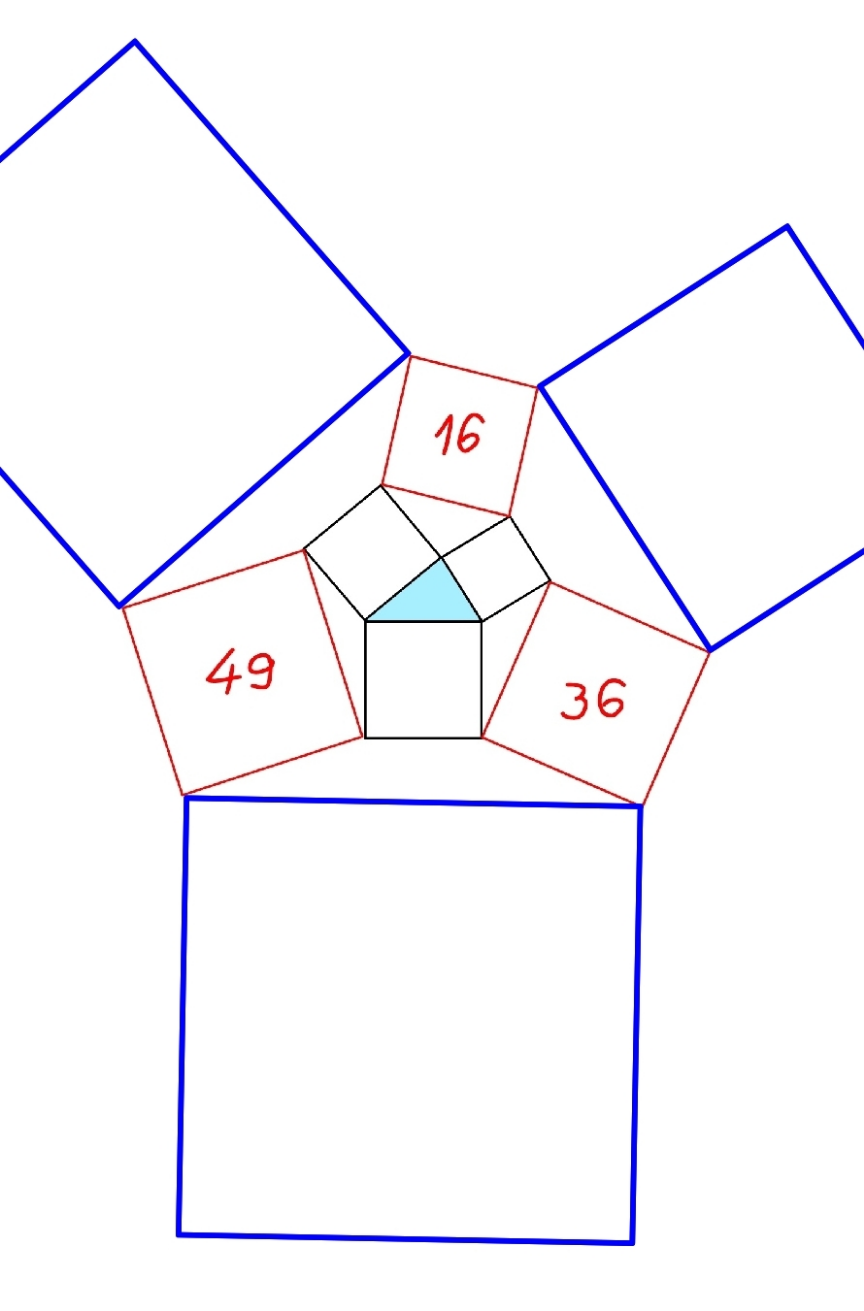
Question Number 180756 Answers: 3 Comments: 1

Question Number 180623 Answers: 1 Comments: 0
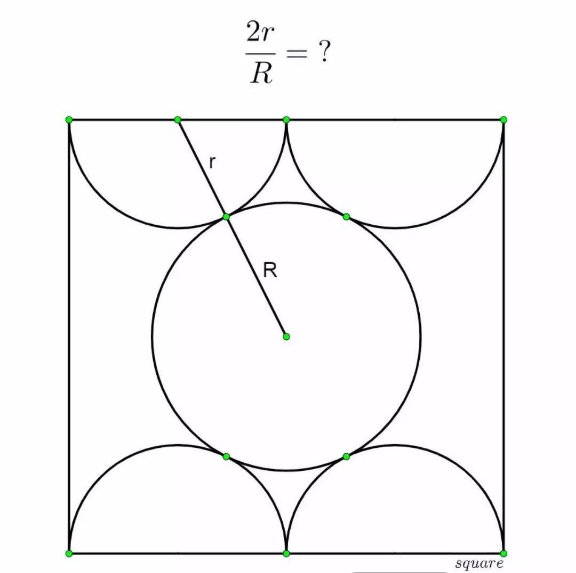
Question Number 180615 Answers: 3 Comments: 0

Question Number 180582 Answers: 1 Comments: 0

Question Number 180547 Answers: 1 Comments: 0
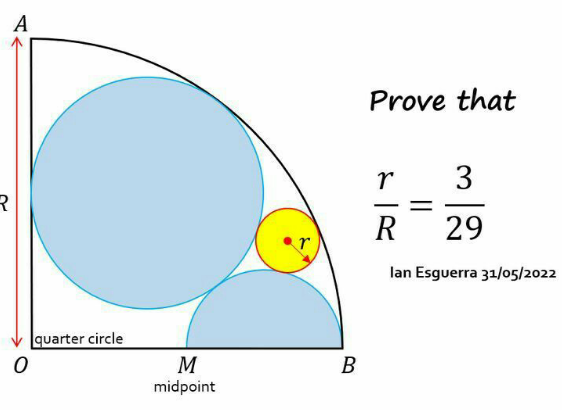
Question Number 180510 Answers: 2 Comments: 1
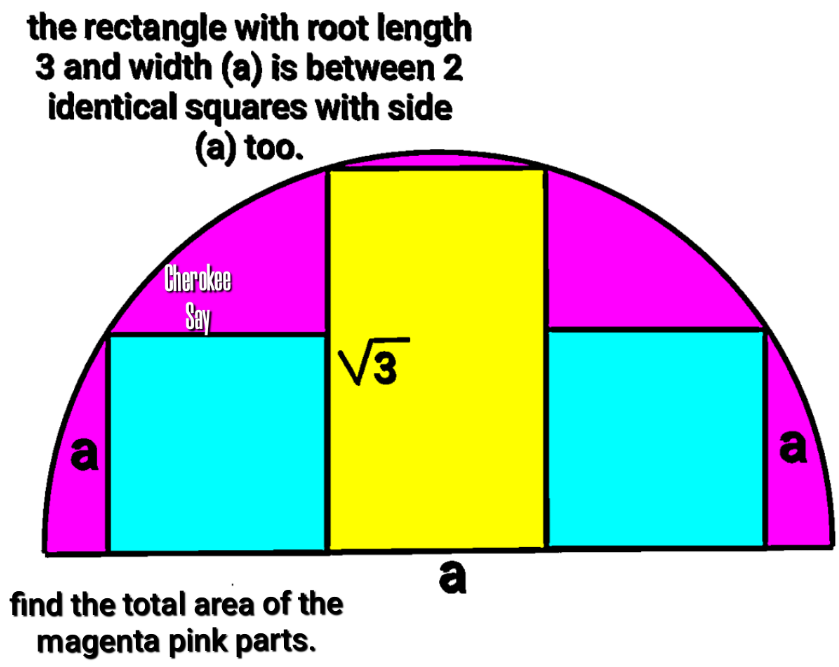
Question Number 180459 Answers: 2 Comments: 0

Question Number 180458 Answers: 2 Comments: 0

Question Number 180423 Answers: 2 Comments: 4

Question Number 180400 Answers: 2 Comments: 1
Question Number 180365 Answers: 1 Comments: 0