
GeometryQuestion and Answers: Page 115
Question Number 13127 Answers: 0 Comments: 0
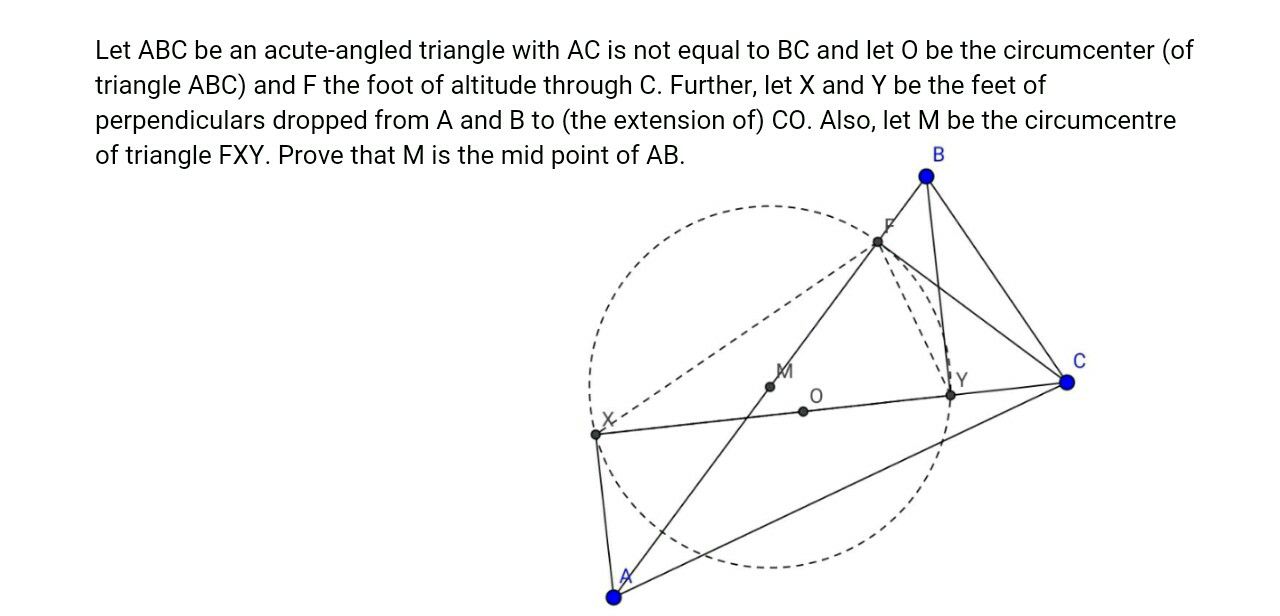
Question Number 13067 Answers: 0 Comments: 4

Question Number 13005 Answers: 1 Comments: 0
Question Number 12875 Answers: 0 Comments: 3
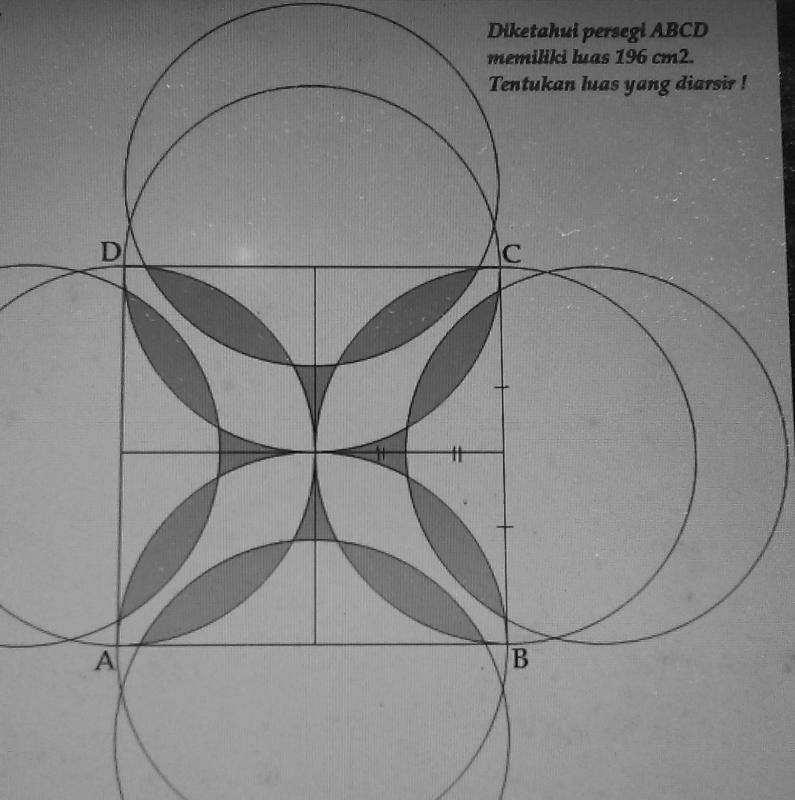
Question Number 12846 Answers: 2 Comments: 1
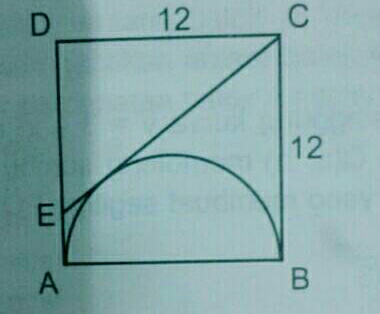
Question Number 12822 Answers: 1 Comments: 0
Question Number 12725 Answers: 3 Comments: 4
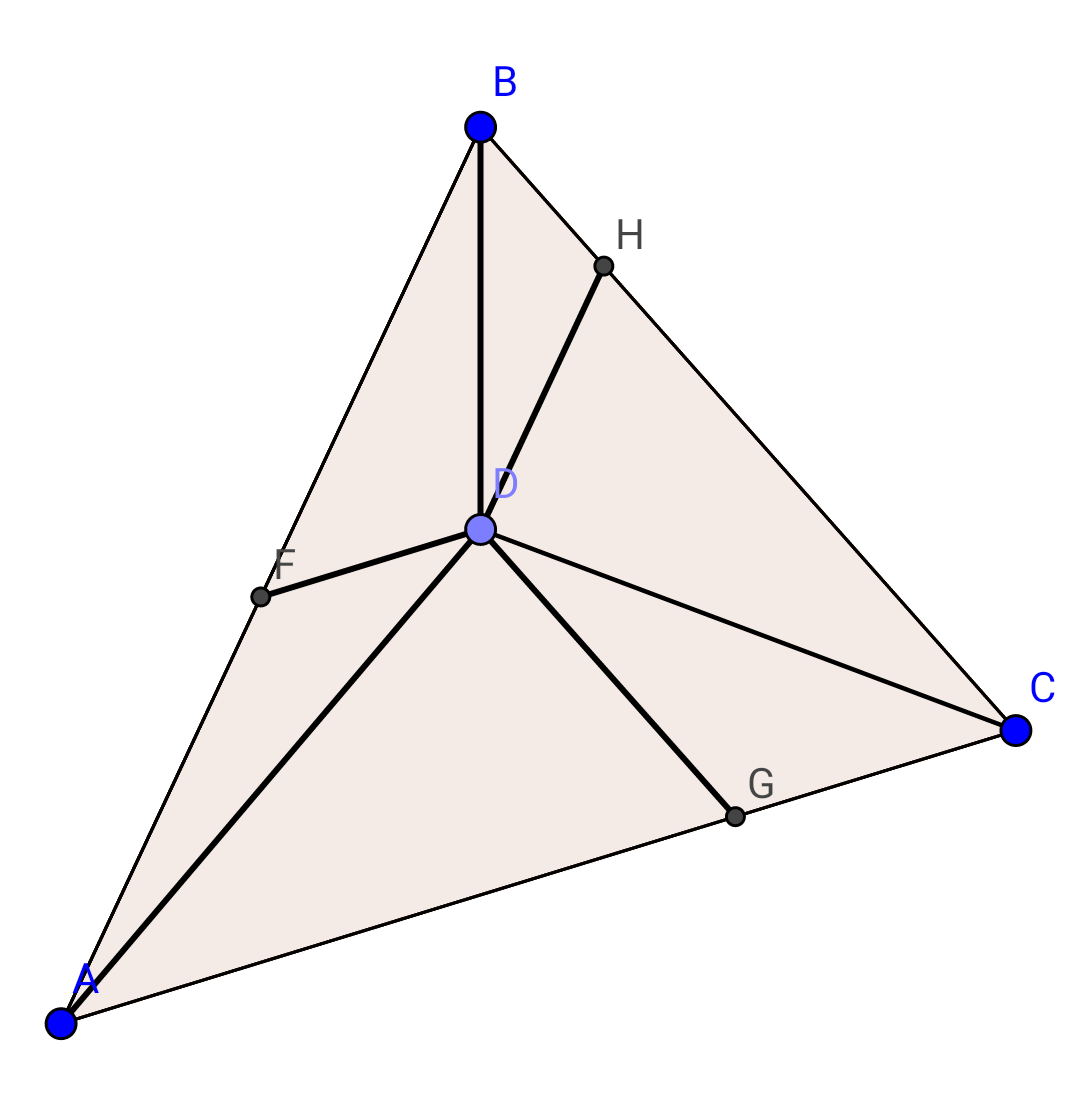
Question Number 12569 Answers: 0 Comments: 0
Question Number 12566 Answers: 1 Comments: 0
Question Number 12553 Answers: 0 Comments: 0
Question Number 12534 Answers: 1 Comments: 0
Question Number 12506 Answers: 2 Comments: 0
Question Number 12490 Answers: 0 Comments: 1
Question Number 12499 Answers: 1 Comments: 0
Question Number 12371 Answers: 0 Comments: 0
Question Number 12332 Answers: 2 Comments: 7
$$\mathrm{prove}\:;\:\left(\frac{\mathrm{0}}{\mathrm{0}}\right)=\mathrm{2} \\ $$
Question Number 12267 Answers: 2 Comments: 0
Question Number 12265 Answers: 0 Comments: 2
Question Number 12148 Answers: 0 Comments: 13
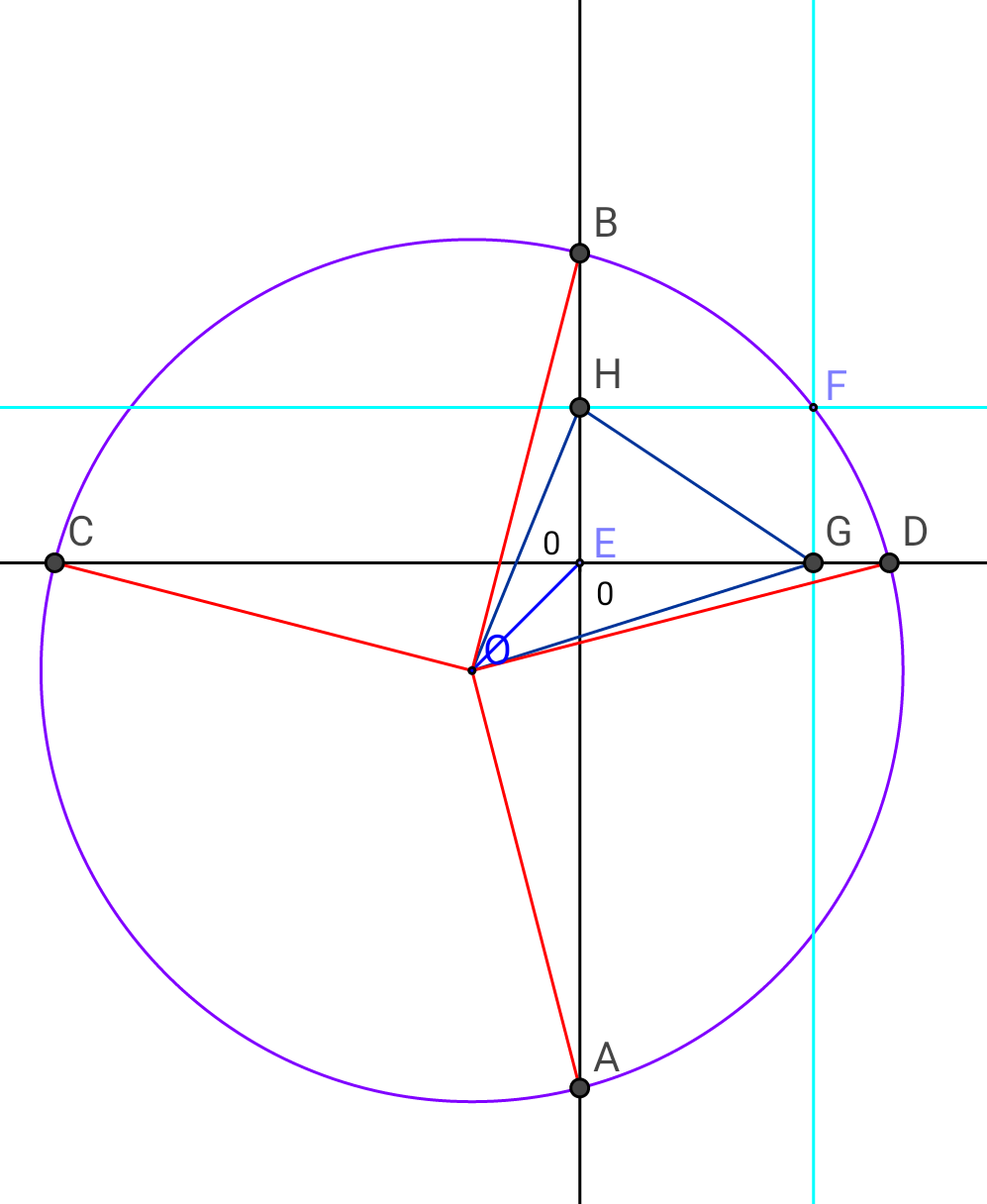
Question Number 12131 Answers: 0 Comments: 0
Question Number 12045 Answers: 1 Comments: 0
Question Number 12019 Answers: 1 Comments: 0

Question Number 12013 Answers: 1 Comments: 0
Question Number 12008 Answers: 1 Comments: 1

Question Number 11991 Answers: 0 Comments: 0
Question Number 11969 Answers: 2 Comments: 0
Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116 Pg 117 Pg 118 Pg 119
