
GeometryQuestion and Answers: Page 114
Question Number 15440 Answers: 3 Comments: 9

Question Number 15434 Answers: 1 Comments: 8

Question Number 15318 Answers: 2 Comments: 6

Question Number 15175 Answers: 2 Comments: 1

Question Number 15170 Answers: 2 Comments: 2

Question Number 15017 Answers: 0 Comments: 0
Question Number 14965 Answers: 2 Comments: 2

Question Number 14964 Answers: 0 Comments: 0
Question Number 15212 Answers: 1 Comments: 1
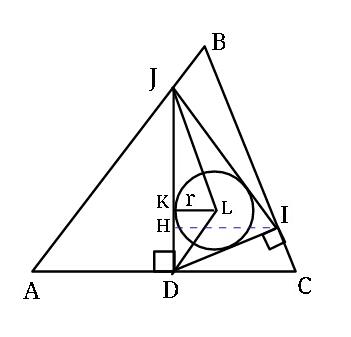
Question Number 14940 Answers: 2 Comments: 12
Question Number 14905 Answers: 0 Comments: 5
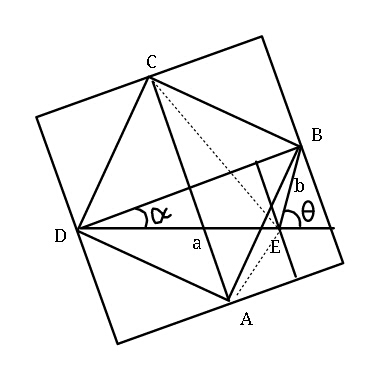
Question Number 14863 Answers: 1 Comments: 8

Question Number 14810 Answers: 0 Comments: 0
Question Number 14809 Answers: 1 Comments: 2
Question Number 14807 Answers: 0 Comments: 0
Question Number 14797 Answers: 1 Comments: 12
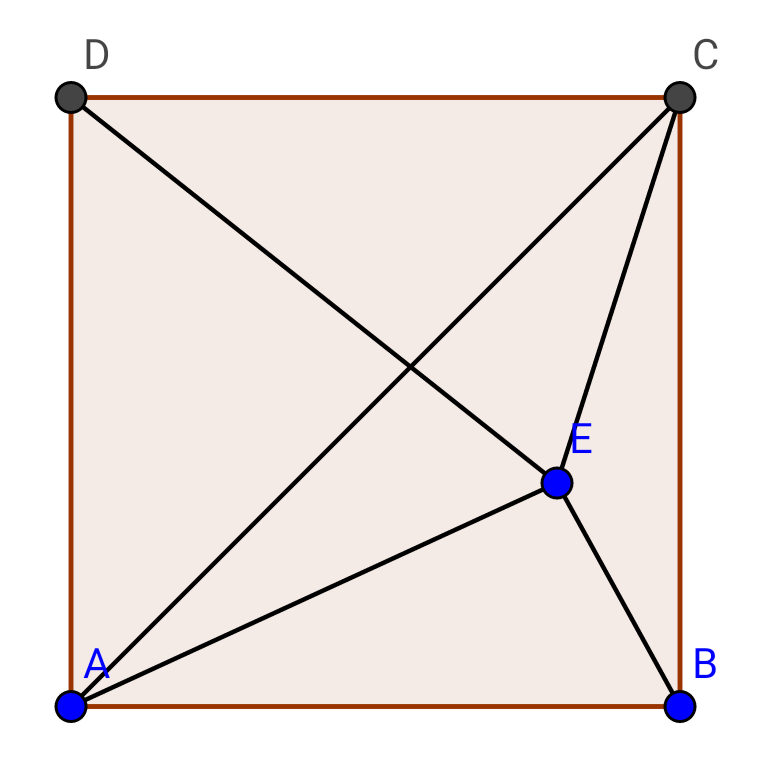
Question Number 14724 Answers: 2 Comments: 1

Question Number 14661 Answers: 1 Comments: 1
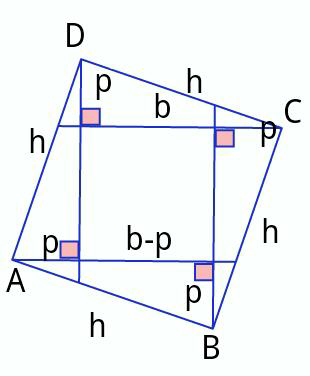
Question Number 14630 Answers: 0 Comments: 2
Question Number 14502 Answers: 1 Comments: 3

Question Number 14384 Answers: 0 Comments: 6

Question Number 14365 Answers: 0 Comments: 1
Question Number 14364 Answers: 0 Comments: 9
Question Number 14145 Answers: 1 Comments: 1

Question Number 14104 Answers: 0 Comments: 0

Question Number 14071 Answers: 2 Comments: 1
Pg 109 Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116 Pg 117 Pg 118
