
GeometryQuestion and Answers: Page 112
Question Number 16592 Answers: 1 Comments: 1
Question Number 16579 Answers: 0 Comments: 3

Question Number 16570 Answers: 0 Comments: 1
Question Number 16483 Answers: 0 Comments: 12
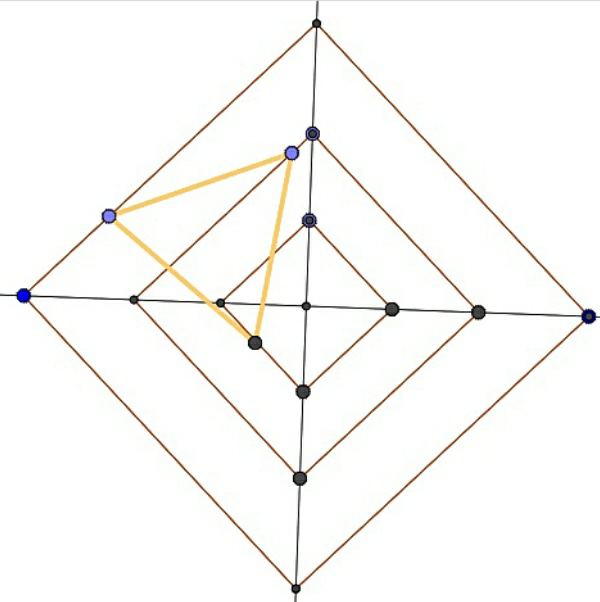
Question Number 16464 Answers: 0 Comments: 2
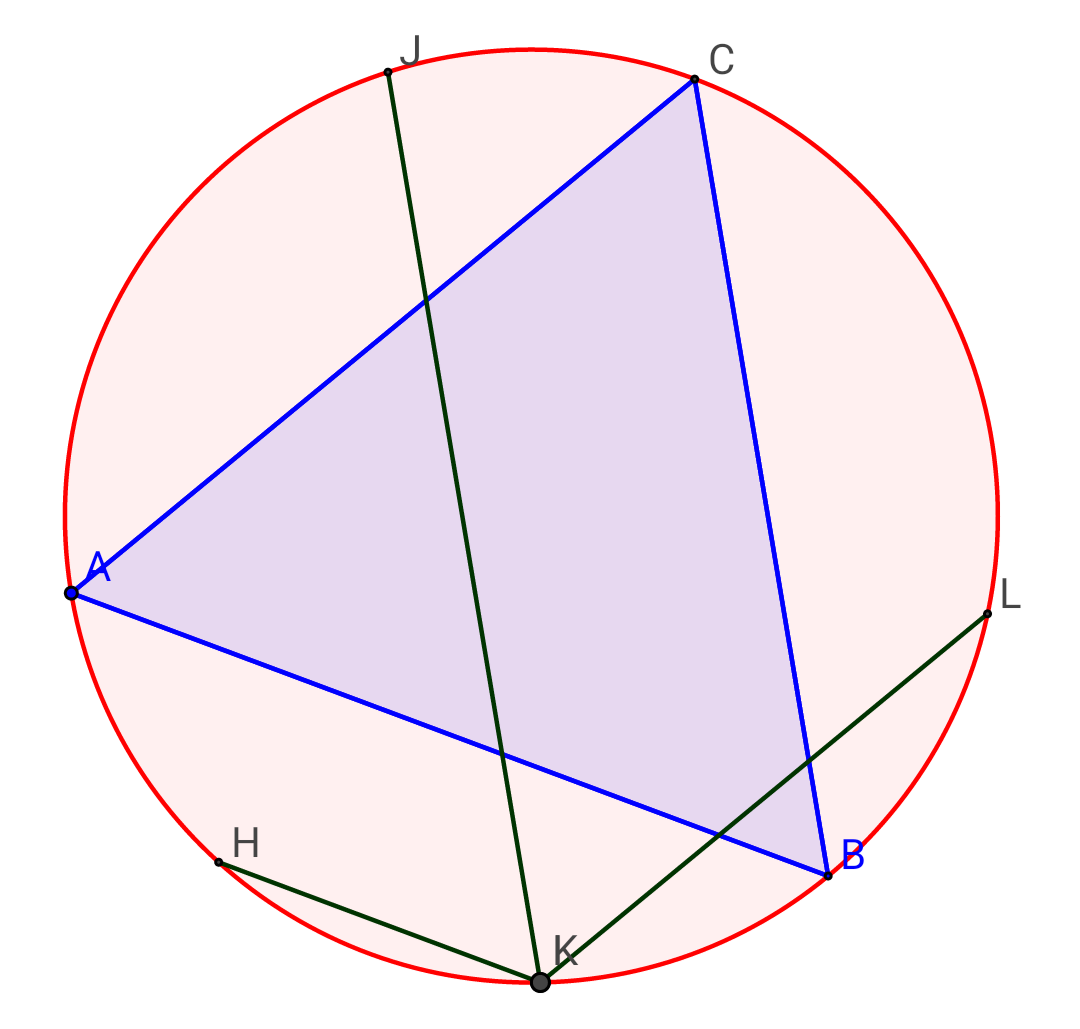
Question Number 16409 Answers: 3 Comments: 9
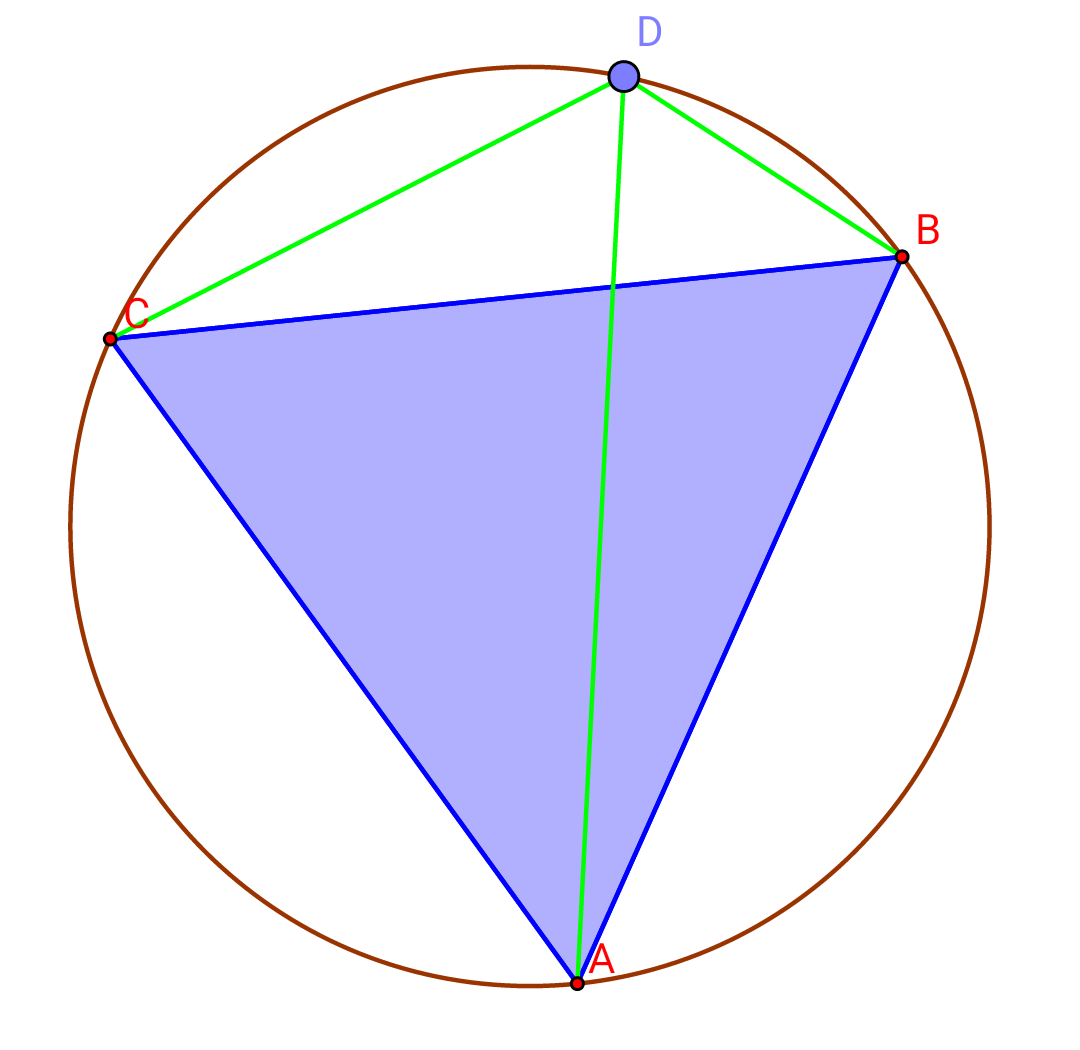
Question Number 16364 Answers: 1 Comments: 0
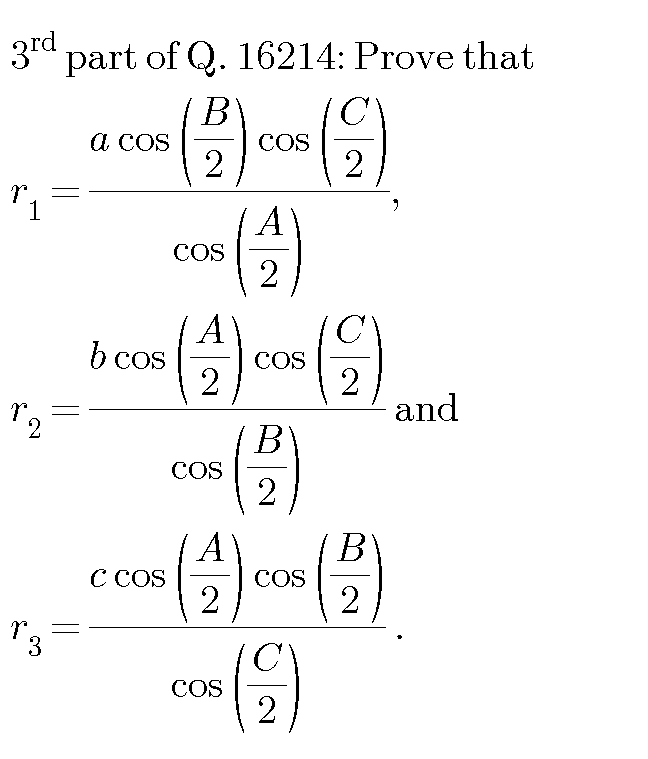
Question Number 16441 Answers: 1 Comments: 2

Question Number 16302 Answers: 1 Comments: 5
Question Number 16277 Answers: 3 Comments: 1
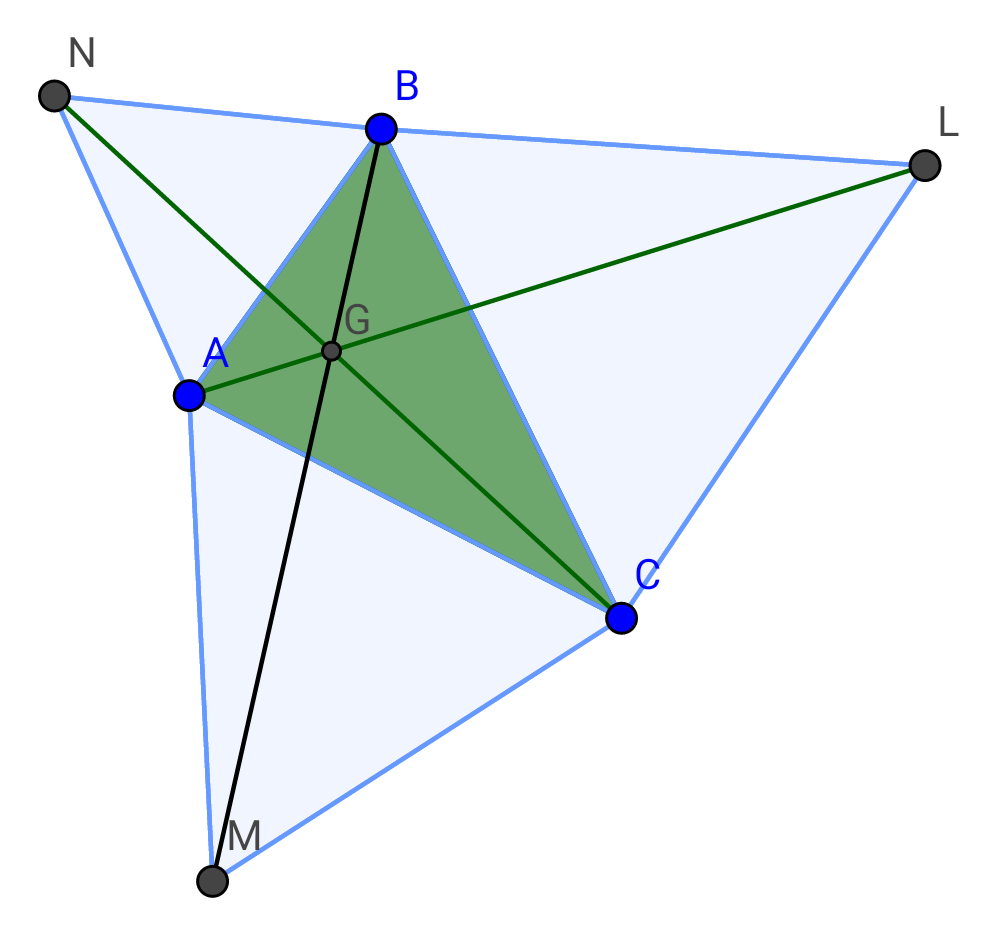
Question Number 16226 Answers: 0 Comments: 1
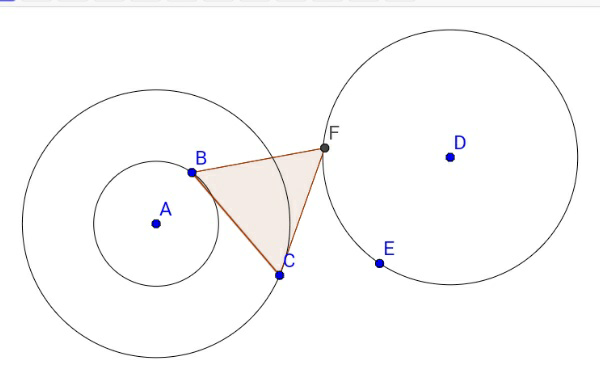
Question Number 16214 Answers: 2 Comments: 4
Question Number 16194 Answers: 0 Comments: 21

Question Number 16140 Answers: 2 Comments: 0

Question Number 16110 Answers: 0 Comments: 1
Question Number 16108 Answers: 1 Comments: 1

Question Number 16077 Answers: 0 Comments: 0
Question Number 16075 Answers: 0 Comments: 0
Question Number 16074 Answers: 0 Comments: 0
Question Number 16072 Answers: 1 Comments: 3
Question Number 16071 Answers: 1 Comments: 0
Question Number 16070 Answers: 0 Comments: 0
Question Number 16069 Answers: 0 Comments: 0
Question Number 16068 Answers: 2 Comments: 0
Question Number 16067 Answers: 1 Comments: 8
Question Number 16066 Answers: 2 Comments: 0
Pg 107 Pg 108 Pg 109 Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115 Pg 116
