Question and Answers Forum

GeometryQuestion and Answers: Page 111

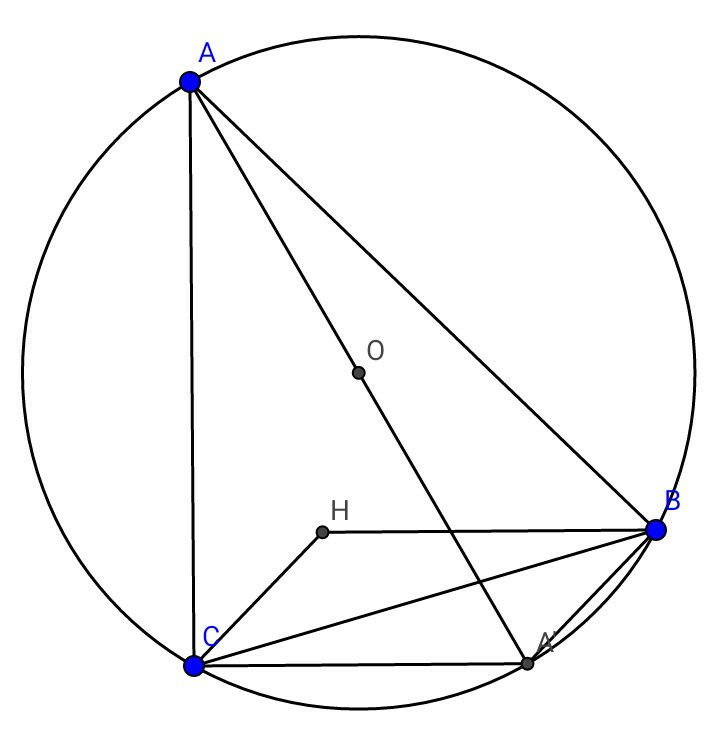
Question Number 16756 Answers: 2 Comments: 1

Alternate vertices of a regular hexagon are joined as shown. What fraction of the total area of the hexagon is shaded? (Justify your answer.)

$$\mathrm{Alternate}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{a}\:\mathrm{regular}\:\mathrm{hexagon} \\ $$$$\mathrm{are}\:\mathrm{joined}\:\mathrm{as}\:\mathrm{shown}.\:\mathrm{What}\:\mathrm{fraction}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{total}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{hexagon}\:\mathrm{is} \\ $$$$\mathrm{shaded}?\:\left(\mathrm{Justify}\:\mathrm{your}\:\mathrm{answer}.\right) \\ $$

Question Number 16740 Answers: 1 Comments: 3

The maximum value of cos^2 (cos (33π + θ)) + sin^2 (sin (45π + θ)) is (1) 1 + sin^2 1 (2) 2 (3) 1 + cos^2 1 (4) cos^2 2

$$\mathrm{The}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{of} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{cos}\:\left(\mathrm{33}\pi\:+\:\theta\right)\right)\:+\:\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{sin}\:\left(\mathrm{45}\pi\:+\:\theta\right)\right) \\ $$$$\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{1}\:+\:\mathrm{sin}^{\mathrm{2}} \mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{2} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{1}\:+\:\mathrm{cos}^{\mathrm{2}} \mathrm{1} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{cos}^{\mathrm{2}} \mathrm{2} \\ $$

Question Number 16739 Answers: 0 Comments: 0

Let M be a point in the interior of the equilateral triangle ABC and let A′, B′ and C′ be its projections onto the sides BC, CA and AB, respectively. Prove that the sum of lengths of the inradii of triangles MAC′, MBA′ and MCB′ equals the sum of lengths of the inradii of trianges MAB′, MBC′ and MCA′.

$$\mathrm{Let}\:{M}\:\mathrm{be}\:\mathrm{a}\:\mathrm{point}\:\mathrm{in}\:\mathrm{the}\:\mathrm{interior}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equilateral}\:\mathrm{triangle}\:{ABC}\:\mathrm{and}\:\mathrm{let}\:{A}', \\ $$$${B}'\:\mathrm{and}\:{C}'\:\mathrm{be}\:\mathrm{its}\:\mathrm{projections}\:\mathrm{onto}\:\mathrm{the} \\ $$$$\mathrm{sides}\:{BC},\:{CA}\:\mathrm{and}\:{AB},\:\mathrm{respectively}. \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{lengths}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{inradii}\:\mathrm{of}\:\mathrm{triangles}\:{MAC}',\:{MBA}'\:\mathrm{and} \\ $$$${MCB}'\:\mathrm{equals}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{lengths}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{inradii}\:\mathrm{of}\:\mathrm{trianges}\:{MAB}',\:{MBC}'\:\mathrm{and} \\ $$$${MCA}'. \\ $$

Question Number 16738 Answers: 0 Comments: 0

Prove that the segments joining the midpoints of the opposite sides of an equiangular hexagon are concurrent.

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{segments}\:\mathrm{joining}\:\mathrm{the} \\ $$$$\mathrm{midpoints}\:\mathrm{of}\:\mathrm{the}\:\mathrm{opposite}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{an} \\ $$$$\mathrm{equiangular}\:\mathrm{hexagon}\:\mathrm{are}\:\mathrm{concurrent}. \\ $$

Question Number 16737 Answers: 0 Comments: 0

A convex hexagon is given in which any two opposite sides have the following property: the distance between their midpoints is ((√3)/2) times the sum of their lengths. Prove that the hexagon is equiangular.

$$\mathrm{A}\:\mathrm{convex}\:\mathrm{hexagon}\:\mathrm{is}\:\mathrm{given}\:\mathrm{in}\:\mathrm{which} \\ $$$$\mathrm{any}\:\mathrm{two}\:\mathrm{opposite}\:\mathrm{sides}\:\mathrm{have}\:\mathrm{the} \\ $$$$\mathrm{following}\:\mathrm{property}:\:\mathrm{the}\:\mathrm{distance} \\ $$$$\mathrm{between}\:\mathrm{their}\:\mathrm{midpoints}\:\mathrm{is}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{times}\:\mathrm{the} \\ $$$$\mathrm{sum}\:\mathrm{of}\:\mathrm{their}\:\mathrm{lengths}.\:\mathrm{Prove}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{hexagon}\:\mathrm{is}\:\mathrm{equiangular}. \\ $$

Question Number 16736 Answers: 0 Comments: 0

The side lengths of an equiangular octagon are rational numbers. Prove that the octagon has a symmetry center.

$$\mathrm{The}\:\mathrm{side}\:\mathrm{lengths}\:\mathrm{of}\:\mathrm{an}\:\mathrm{equiangular} \\ $$$$\mathrm{octagon}\:\mathrm{are}\:\mathrm{rational}\:\mathrm{numbers}.\:\mathrm{Prove} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{octagon}\:\mathrm{has}\:\mathrm{a}\:\mathrm{symmetry} \\ $$$$\mathrm{center}. \\ $$

Question Number 16735 Answers: 0 Comments: 0

Let a_1 , a_2 , ..., a_n be the side lengths of an equiangular polygon. Prove that if a_1 ≥ a_2 ≥ ... ≥ a_n , then the polygon is regular.

$$\mathrm{Let}\:{a}_{\mathrm{1}} ,\:{a}_{\mathrm{2}} ,\:...,\:{a}_{{n}} \:\mathrm{be}\:\mathrm{the}\:\mathrm{side}\:\mathrm{lengths}\:\mathrm{of}\: \\ $$$$\mathrm{an}\:\mathrm{equiangular}\:\mathrm{polygon}.\:\mathrm{Prove}\:\mathrm{that}\:\mathrm{if} \\ $$$${a}_{\mathrm{1}} \:\geqslant\:{a}_{\mathrm{2}} \:\geqslant\:...\:\geqslant\:{a}_{{n}} ,\:\mathrm{then}\:\mathrm{the}\:\mathrm{polygon}\:\mathrm{is} \\ $$$$\mathrm{regular}. \\ $$

Question Number 16734 Answers: 0 Comments: 0

An equiangular polygon with an odd number of sides is inscribed in a circle. Prove that the polygon is regular.

$$\mathrm{An}\:\mathrm{equiangular}\:\mathrm{polygon}\:\mathrm{with}\:\mathrm{an}\:\mathrm{odd} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{sides}\:\mathrm{is}\:\mathrm{inscribed}\:\mathrm{in}\:\mathrm{a}\:\mathrm{circle}. \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{polygon}\:\mathrm{is}\:\mathrm{regular}. \\ $$

Question Number 16754 Answers: 2 Comments: 1

Question Number 16665 Answers: 0 Comments: 1

Question Number 16641 Answers: 0 Comments: 0

Prove that p is a prime number if and only if every equiangular polygon with p sides of rational lengths is regular.

$$\mathrm{Prove}\:\mathrm{that}\:{p}\:\mathrm{is}\:\mathrm{a}\:\mathrm{prime}\:\mathrm{number}\:\mathrm{if}\:\mathrm{and} \\ $$$$\mathrm{only}\:\mathrm{if}\:\mathrm{every}\:\mathrm{equiangular}\:\mathrm{polygon}\:\mathrm{with} \\ $$$${p}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{rational}\:\mathrm{lengths}\:\mathrm{is}\:\mathrm{regular}. \\ $$

Question Number 16595 Answers: 1 Comments: 4

Question Number 16592 Answers: 1 Comments: 1

please what does the question mean by the overlapping portion of A and B.

$$\mathrm{please}\:\mathrm{what}\:\mathrm{does}\:\mathrm{the}\:\mathrm{question}\:\mathrm{mean} \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{overlapping}\:\mathrm{portion}\:\mathrm{of}\:\mathrm{A}\: \\ $$$$\mathrm{and}\:\mathrm{B}. \\ $$

Question Number 16579 Answers: 0 Comments: 3

Question Number 16570 Answers: 0 Comments: 1

A,B and E are three circles all with radius 1 unit.A and E touch at P whole B and E touch at Q. ∠POQ=x° where O is the centre of E.Find the area of the overlapping portion of A and B if 0≤x≤60°

$$\mathrm{A},\mathrm{B}\:\mathrm{and}\:\mathrm{E}\:\mathrm{are}\:\mathrm{three}\:\mathrm{circles}\:\mathrm{all}\: \\ $$$$\mathrm{with}\:\mathrm{radius}\:\mathrm{1}\:\mathrm{unit}.\mathrm{A}\:\mathrm{and}\:\mathrm{E}\:\mathrm{touch} \\ $$$$\mathrm{at}\:\mathrm{P}\:\mathrm{whole}\:\mathrm{B}\:\mathrm{and}\:\mathrm{E}\:\mathrm{touch}\:\mathrm{at}\:\mathrm{Q}. \\ $$$$\angle\mathrm{POQ}=\mathrm{x}°\:\mathrm{where}\:\mathrm{O}\:\mathrm{is}\:\mathrm{the}\:\mathrm{centre}\: \\ $$$$\mathrm{of}\:\mathrm{E}.\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{overlapping}\:\mathrm{portion}\:\mathrm{of}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{if} \\ $$$$\mathrm{0}\leqslant\mathrm{x}\leqslant\mathrm{60}° \\ $$

Question Number 16483 Answers: 0 Comments: 12

Question Number 16464 Answers: 0 Comments: 2

Question Number 16409 Answers: 3 Comments: 9

Question Number 16364 Answers: 1 Comments: 0

Question Number 16441 Answers: 1 Comments: 2

Question Number 16302 Answers: 1 Comments: 5

Related to Q16140 What if the three lines d_1 ,d_2 ,d_3 are not parallel, but concurrent?

Question Number 16277 Answers: 3 Comments: 1

Question Number 16226 Answers: 0 Comments: 1

Question Number 16214 Answers: 2 Comments: 4

In ΔABC, r_1 , r_2 and r_3 are the exradii as shown. Prove that r_1 = (Δ/(s − a)) , r_2 = (Δ/(s − b)) and r_3 = (Δ/(s − c)) . Here s = ((a + b + c)/2) .

$$\mathrm{In}\:\Delta{ABC},\:{r}_{\mathrm{1}} ,\:{r}_{\mathrm{2}} \:\mathrm{and}\:{r}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{exradii} \\ $$$$\mathrm{as}\:\mathrm{shown}.\:\mathrm{Prove}\:\mathrm{that}\:{r}_{\mathrm{1}} \:=\:\frac{\Delta}{{s}\:−\:{a}}\:, \\ $$$${r}_{\mathrm{2}} \:=\:\frac{\Delta}{{s}\:−\:{b}}\:\mathrm{and}\:{r}_{\mathrm{3}} \:=\:\frac{\Delta}{{s}\:−\:{c}}\:.\:\mathrm{Here} \\ $$$${s}\:=\:\frac{{a}\:+\:{b}\:+\:{c}}{\mathrm{2}}\:. \\ $$

Question Number 16194 Answers: 0 Comments: 21

Question Number 16140 Answers: 2 Comments: 0

Pg 106 Pg 107 Pg 108 Pg 109 Pg 110 Pg 111 Pg 112 Pg 113 Pg 114 Pg 115

Contact: info@tinkutara.com