
GeometryQuestion and Answers: Page 110
Question Number 17948 Answers: 1 Comments: 3

Question Number 17886 Answers: 0 Comments: 7

Question Number 17884 Answers: 1 Comments: 1
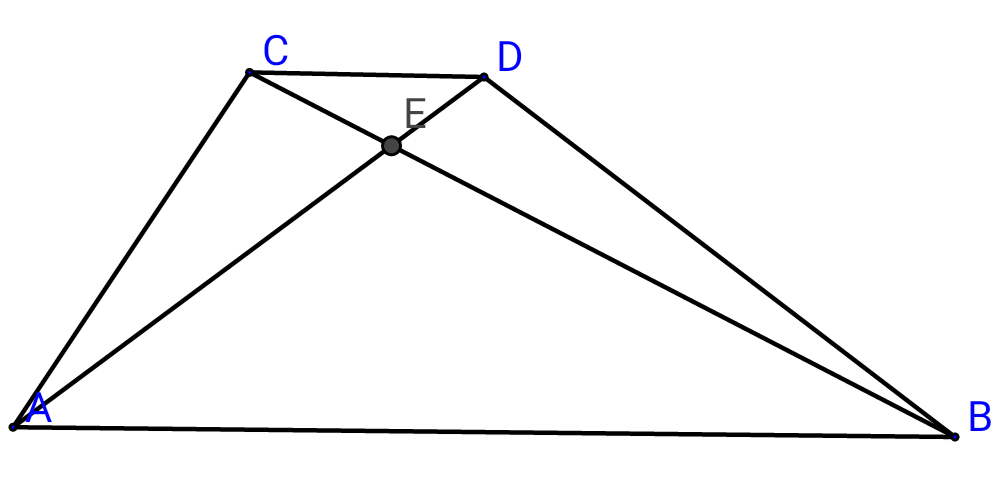
Question Number 17935 Answers: 0 Comments: 0
Question Number 17771 Answers: 1 Comments: 1

Question Number 17743 Answers: 2 Comments: 0

Question Number 17692 Answers: 1 Comments: 0

Question Number 17653 Answers: 0 Comments: 6
Question Number 17614 Answers: 0 Comments: 3
Question Number 17580 Answers: 0 Comments: 8
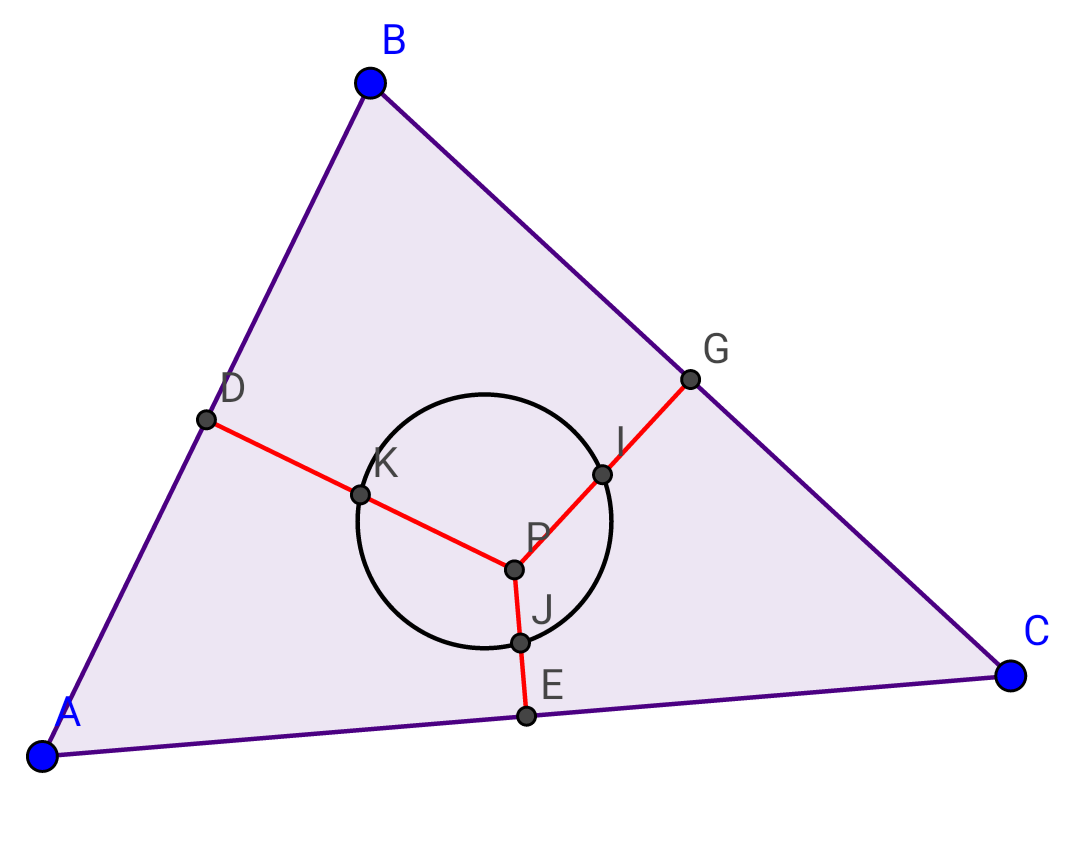
Question Number 17524 Answers: 1 Comments: 0
Question Number 17520 Answers: 1 Comments: 1
Question Number 17449 Answers: 1 Comments: 4
Question Number 17440 Answers: 1 Comments: 0
Question Number 17645 Answers: 2 Comments: 1
Question Number 17373 Answers: 2 Comments: 0
Question Number 17273 Answers: 1 Comments: 2
Question Number 17177 Answers: 1 Comments: 0

Question Number 17158 Answers: 0 Comments: 4
Question Number 16980 Answers: 0 Comments: 1
Question Number 16958 Answers: 0 Comments: 0
Question Number 16951 Answers: 0 Comments: 0
Question Number 16947 Answers: 0 Comments: 0
Question Number 16946 Answers: 0 Comments: 0
Question Number 16940 Answers: 1 Comments: 1
Question Number 16882 Answers: 0 Comments: 2
Pg 105 Pg 106 Pg 107 Pg 108 Pg 109 Pg 110 Pg 111 Pg 112 Pg 113 Pg 114
