
GeometryQuestion and Answers: Page 109
Question Number 19709 Answers: 1 Comments: 0
Question Number 19783 Answers: 1 Comments: 3
Question Number 19699 Answers: 0 Comments: 0
Question Number 19668 Answers: 0 Comments: 2

Question Number 19659 Answers: 1 Comments: 0
Question Number 19415 Answers: 1 Comments: 0
Question Number 19394 Answers: 1 Comments: 0
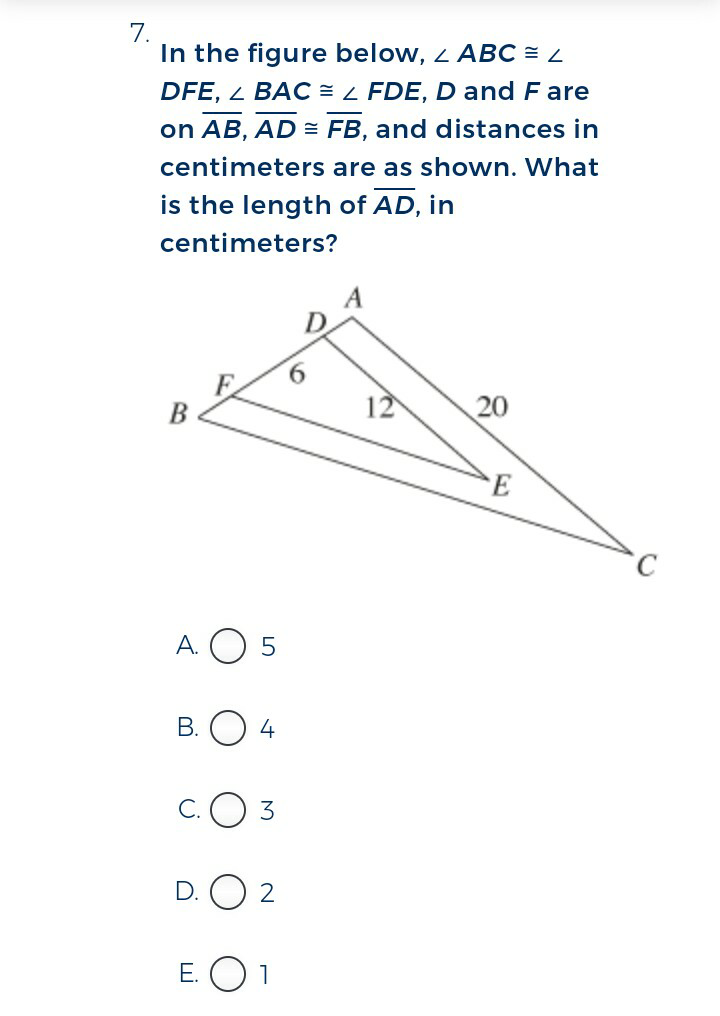
Question Number 19388 Answers: 0 Comments: 1
Question Number 19301 Answers: 1 Comments: 0
Question Number 19293 Answers: 1 Comments: 3
Question Number 19279 Answers: 0 Comments: 0
Question Number 19150 Answers: 1 Comments: 4
Question Number 19104 Answers: 1 Comments: 1
Question Number 18801 Answers: 0 Comments: 1
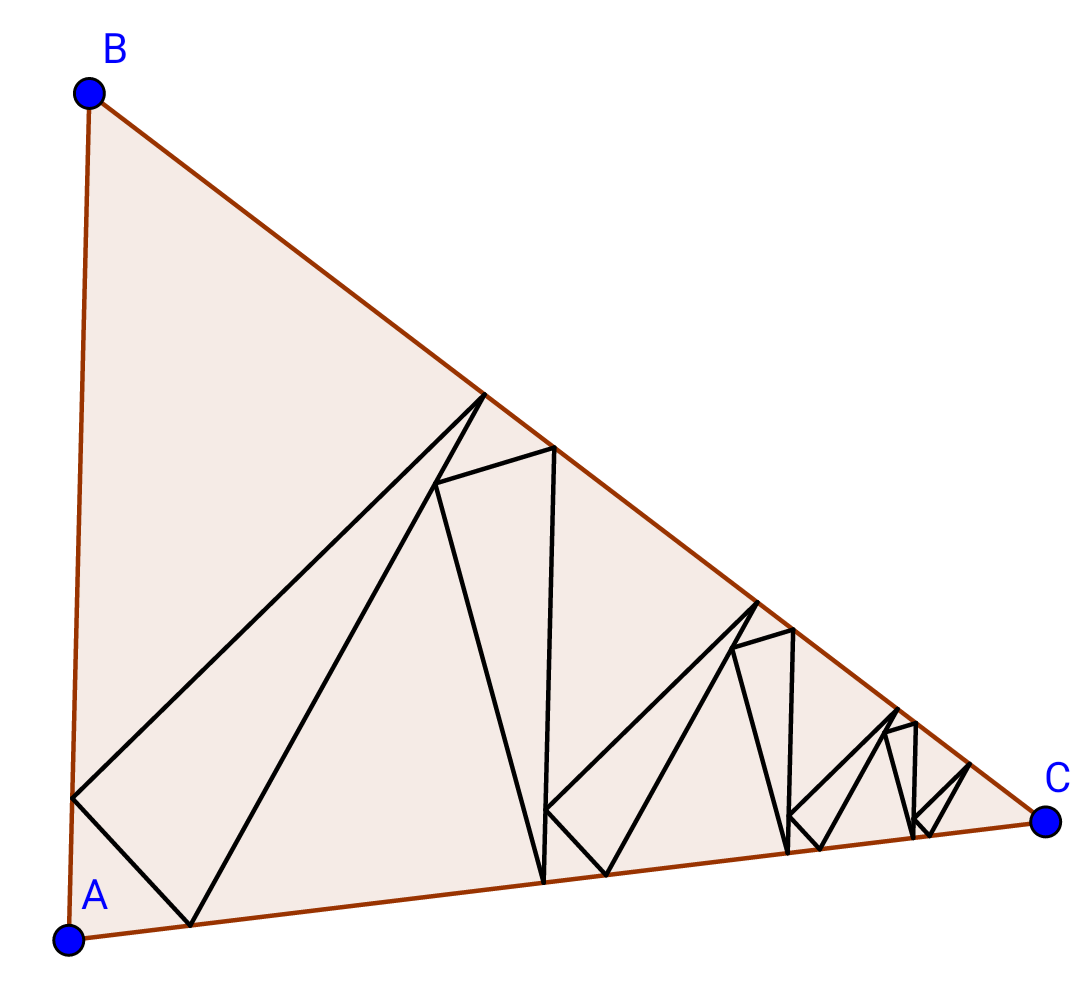
Question Number 18799 Answers: 1 Comments: 0

Question Number 18783 Answers: 1 Comments: 0
Question Number 18967 Answers: 0 Comments: 3
Question Number 18681 Answers: 1 Comments: 0
Question Number 18968 Answers: 1 Comments: 1
Question Number 18625 Answers: 1 Comments: 1
Question Number 19238 Answers: 0 Comments: 4
Question Number 18527 Answers: 0 Comments: 0
Question Number 18477 Answers: 0 Comments: 0
Question Number 18461 Answers: 1 Comments: 0

Question Number 18394 Answers: 0 Comments: 0

Question Number 18323 Answers: 0 Comments: 0
Pg 104 Pg 105 Pg 106 Pg 107 Pg 108 Pg 109 Pg 110 Pg 111 Pg 112 Pg 113
