
GeometryQuestion and Answers: Page 107
Question Number 23133 Answers: 1 Comments: 0
Question Number 23162 Answers: 1 Comments: 1

Question Number 23122 Answers: 0 Comments: 3

Question Number 23050 Answers: 1 Comments: 0
Question Number 23034 Answers: 0 Comments: 1
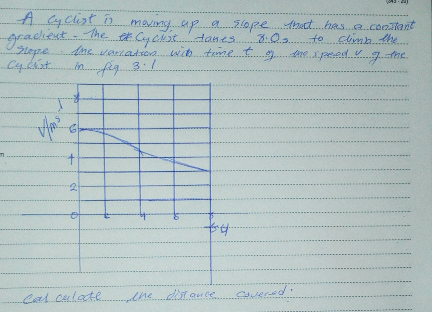
Question Number 22896 Answers: 0 Comments: 1
Question Number 22787 Answers: 0 Comments: 2
Question Number 22661 Answers: 1 Comments: 1

Question Number 23796 Answers: 1 Comments: 0
$$\int\frac{\mathrm{2sinx}+\mathrm{3cosx}}{\mathrm{3sinx}+\mathrm{4cosx}}\:\mathrm{dx} \\ $$
Question Number 22545 Answers: 2 Comments: 0
Question Number 22525 Answers: 0 Comments: 4

Question Number 22524 Answers: 0 Comments: 1
Question Number 22522 Answers: 0 Comments: 1
$$\mathrm{H}{appy}\: \\ $$$${Diwali} \\ $$$$\left.{Friends}\:!!\::\right) \\ $$
Question Number 22516 Answers: 0 Comments: 1
Question Number 22515 Answers: 0 Comments: 0
Question Number 22478 Answers: 0 Comments: 1
Question Number 22361 Answers: 0 Comments: 0

Question Number 23106 Answers: 0 Comments: 0
$${Is}\:\mathrm{2}\left({x}+\mathrm{1}\right)\:{had}\:{a}\:{x}=\mathrm{3} \\ $$
Question Number 22112 Answers: 1 Comments: 0
Question Number 22079 Answers: 0 Comments: 1
Question Number 22055 Answers: 0 Comments: 1
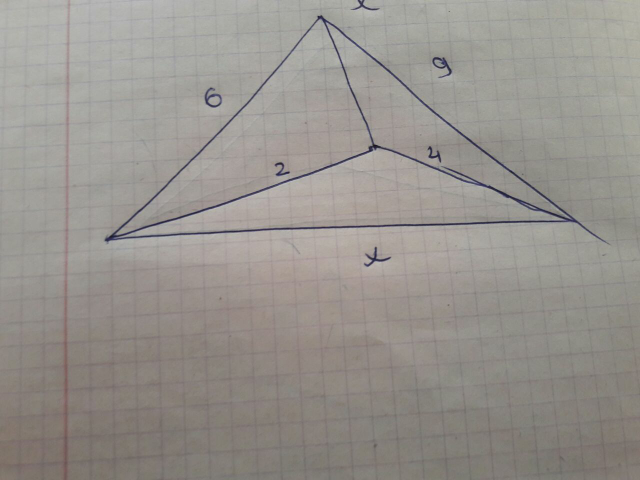
Question Number 22001 Answers: 1 Comments: 0
Question Number 21973 Answers: 1 Comments: 1
Question Number 21903 Answers: 0 Comments: 0
Question Number 21840 Answers: 1 Comments: 0
Question Number 21825 Answers: 0 Comments: 2
Pg 102 Pg 103 Pg 104 Pg 105 Pg 106 Pg 107 Pg 108 Pg 109 Pg 110 Pg 111
