Question and Answers Forum

All Questions Topic List

GeometryQuestion and Answers: Page 106

Question Number 23592 Answers: 1 Comments: 0

Let ABC be a triangle with AB = AC and ∠BAC = 30°. Let A′ be the reflection of A in the line BC; B′ be the reflection of B in the line CA; C′ be the reflection of C in the line AB. Show that A′, B′, C′ form the vertices of an equilateral triangle.

$$\mathrm{Let}\:{ABC}\:\mathrm{be}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{with}\:{AB}\:=\:{AC} \\ $$$$\mathrm{and}\:\angle{BAC}\:=\:\mathrm{30}°.\:\mathrm{Let}\:{A}'\:\mathrm{be}\:\mathrm{the}\:\mathrm{reflection} \\ $$$$\mathrm{of}\:{A}\:\mathrm{in}\:\mathrm{the}\:\mathrm{line}\:{BC};\:{B}'\:\mathrm{be}\:\mathrm{the}\:\mathrm{reflection} \\ $$$$\mathrm{of}\:{B}\:\mathrm{in}\:\mathrm{the}\:\mathrm{line}\:{CA};\:{C}'\:\mathrm{be}\:\mathrm{the}\:\mathrm{reflection} \\ $$$$\mathrm{of}\:{C}\:\mathrm{in}\:\mathrm{the}\:\mathrm{line}\:{AB}.\:\mathrm{Show}\:\mathrm{that}\:{A}',\:{B}',\:{C}' \\ $$$$\mathrm{form}\:\mathrm{the}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{an}\:\mathrm{equilateral} \\ $$$$\mathrm{triangle}. \\ $$

Question Number 23539 Answers: 1 Comments: 0

∫tan^6 x dx

$$\int\mathrm{tan}\:^{\mathrm{6}} \mathrm{x}\:\mathrm{dx} \\ $$

Question Number 23477 Answers: 0 Comments: 0

Find the value of x, ∫_(−∞) ^x dx = ∫∣± sinh cot ln (15−(√(33+x)))∣ dx

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x}, \\ $$$$\:\:\:\:\:\:\:\int_{−\infty} ^{{x}} {d}\mathrm{x}\:=\:\int\mid\pm\:\mathrm{sinh}\:\mathrm{cot}\:\mathrm{ln}\:\left(\mathrm{15}−\sqrt{\mathrm{33}+{x}}\right)\mid\:\mathrm{dx} \\ $$

Question Number 23418 Answers: 1 Comments: 0

∫sec^2 (√x) /(√x) dx

$$\int\mathrm{sec}\:^{\mathrm{2}} \sqrt{\mathrm{x}}\:/\sqrt{\mathrm{x}}\:\mathrm{dx} \\ $$

Question Number 23408 Answers: 1 Comments: 0

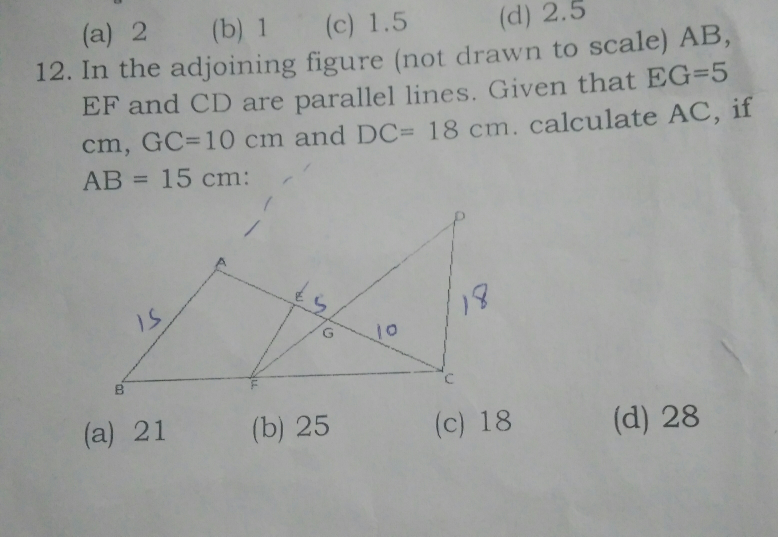
Question Number 23317 Answers: 1 Comments: 0

∫sin^3 x cos x dx

$$\int\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}\:\mathrm{cos}\:\mathrm{x}\:\mathrm{dx} \\ $$

Question Number 23312 Answers: 1 Comments: 2

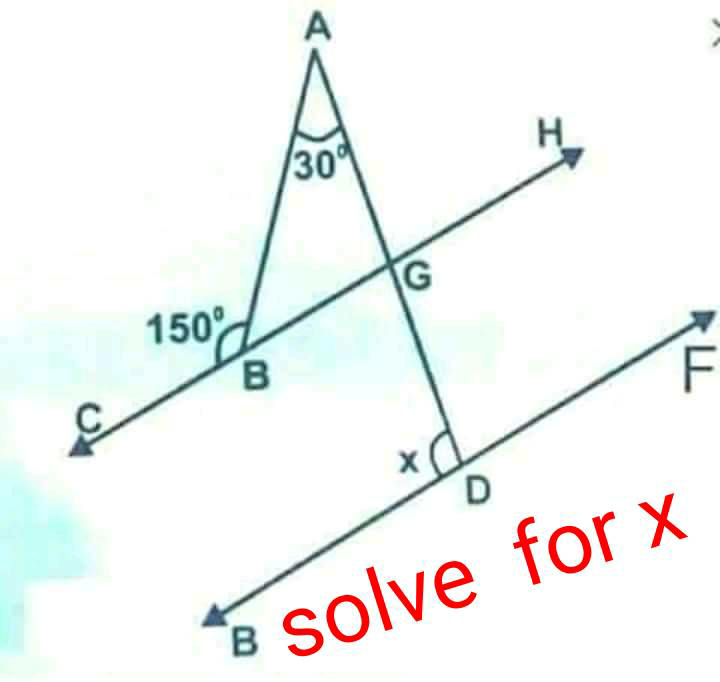
Question Number 23262 Answers: 0 Comments: 2

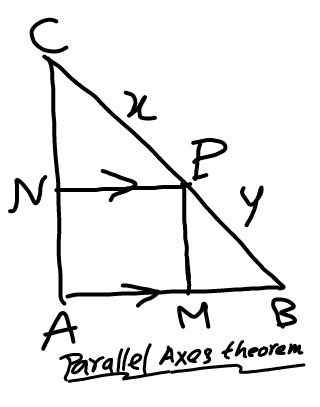
Question Number 23251 Answers: 0 Comments: 1

Question Number 23226 Answers: 1 Comments: 4

Question Number 23253 Answers: 1 Comments: 8

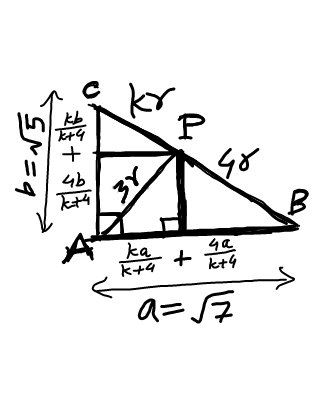
Question Number 23179 Answers: 2 Comments: 1

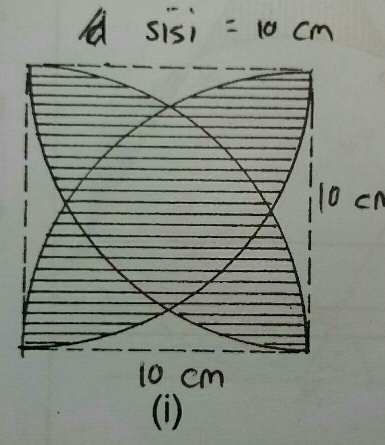
Question Number 23212 Answers: 1 Comments: 1

Question Number 23170 Answers: 0 Comments: 2

Question Number 23138 Answers: 1 Comments: 1

Question Number 23133 Answers: 1 Comments: 0

Find the minimum surface area of a solid circular cylinder , if its volume is 16π cm^3 (leave your answer in terms of π)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{surface}\:\mathrm{area}\:\mathrm{of}\:\mathrm{a}\:\mathrm{solid}\:\mathrm{circular}\:\mathrm{cylinder}\:,\:\:\mathrm{if}\:\mathrm{its}\:\mathrm{volume}\:\mathrm{is} \\ $$$$\mathrm{16}\pi\:\mathrm{cm}^{\mathrm{3}} \:\:\:\left(\mathrm{leave}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\pi\right) \\ $$

Question Number 23162 Answers: 1 Comments: 1

Question Number 23122 Answers: 0 Comments: 3

Question Number 23050 Answers: 1 Comments: 0

how can demonstred that ∀a,b,c∈N a^2 +b^2 =c^2 ⇒ abc≡0[60]

$${how}\:{can}\:{demonstred}\:{that}\: \\ $$$$\:\:\:\forall{a},{b},{c}\in\mathbb{N}\: \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} \:\:\Rightarrow \\ $$$${abc}\equiv\mathrm{0}\left[\mathrm{60}\right]\:\: \\ $$

Question Number 23034 Answers: 0 Comments: 1

Question Number 22896 Answers: 0 Comments: 1

how can demonstred 17^(4n+1) +3×9^(2n+1) ≡0[11]

$${how}\:{can}\:{demonstred} \\ $$$$\mathrm{17}^{\mathrm{4}{n}+\mathrm{1}} +\mathrm{3}×\mathrm{9}^{\mathrm{2}{n}+\mathrm{1}} \equiv\mathrm{0}\left[\mathrm{11}\right] \\ $$

Question Number 22787 Answers: 0 Comments: 2

sin^(−1) (sin 10)=10 or 3π−10 Ans is 3π−10 How

$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:\mathrm{10}\right)=\mathrm{10}\:\mathrm{or}\:\mathrm{3}\pi−\mathrm{10} \\ $$$$\mathrm{Ans}\:\mathrm{is}\:\mathrm{3}\pi−\mathrm{10}\:\:\:\mathrm{How} \\ $$

Question Number 22661 Answers: 1 Comments: 1

Question Number 23796 Answers: 1 Comments: 0

∫((2sinx+3cosx)/(3sinx+4cosx)) dx

$$\int\frac{\mathrm{2sinx}+\mathrm{3cosx}}{\mathrm{3sinx}+\mathrm{4cosx}}\:\mathrm{dx} \\ $$

Question Number 22545 Answers: 2 Comments: 0

∫(x^(1/2) /(x^(1/2) −x^(1/3) ))dx=

$$\int\frac{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{3}}} }\mathrm{dx}= \\ $$$$ \\ $$

Question Number 22525 Answers: 0 Comments: 4

Pg 101 Pg 102 Pg 103 Pg 104 Pg 105 Pg 106 Pg 107 Pg 108 Pg 109 Pg 110

Terms of Service

Contact: info@tinkutara.com