Question and Answers Forum

GeometryQuestion and Answers: Page 105

Question Number 27055 Answers: 1 Comments: 1

Question Number 26858 Answers: 2 Comments: 0

Prove that the internal bisector of an angle of a triangle divides the opposite sides in the ratio of the sides containing the angle.

$${Prove}\:{that}\:{the}\:{internal}\:{bisector}\:{of}\:{an}\:{angle}\: \\ $$$${of}\:{a}\:{triangle}\:{divides}\:{the}\:{opposite} \\ $$$${sides}\:{in}\:{the}\:{ratio}\:{of}\:{the}\:{sides}\:{containing} \\ $$$${the}\:{angle}. \\ $$

Question Number 26824 Answers: 3 Comments: 0

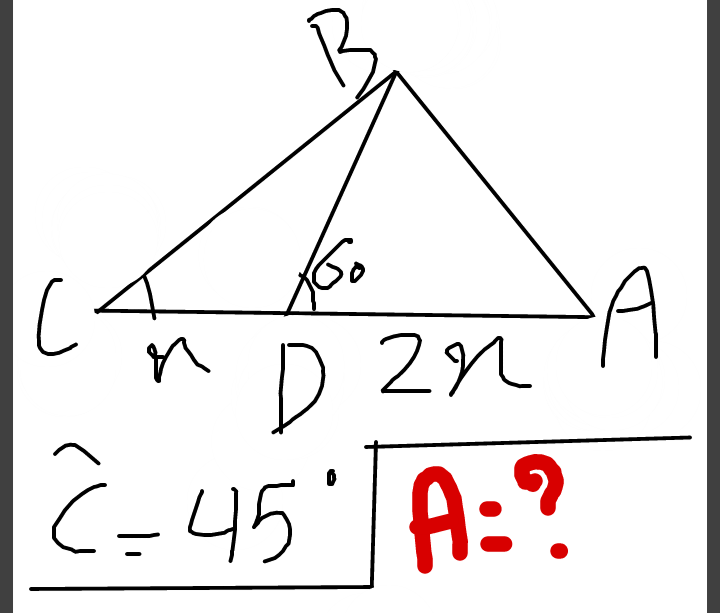
Question Number 26776 Answers: 0 Comments: 2

Question Number 26772 Answers: 1 Comments: 0

With a center on a given circle of radius r ,an arc has been drawn in order to divide the circle in two equal (in area) parts. What is the radius of the arc in terms of r (radius of given circle)?

$$\mathrm{With}\:\mathrm{a}\:\mathrm{center}\:\boldsymbol{\mathrm{on}}\:\mathrm{a}\:\mathrm{given}\:\mathrm{circle}\:\mathrm{of} \\ $$$$\mathrm{radius}\:\mathrm{r}\:,\mathrm{an}\:\mathrm{arc}\:\mathrm{has}\:\mathrm{been}\:\mathrm{drawn}\:\mathrm{in}\:\mathrm{order} \\ $$$$\mathrm{to}\:\mathrm{divide}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{in}\:\mathrm{two}\:\mathrm{equal} \\ $$$$\left(\mathrm{in}\:\mathrm{area}\right)\:\mathrm{parts}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{arc}\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\:\mathrm{r}\:\left(\mathrm{radius}\:\mathrm{of}\:\mathrm{given}\:\mathrm{circle}\right)?\: \\ $$

Question Number 26723 Answers: 0 Comments: 2

Take a point on a given circle as a center and draw an arc which divide the given circle into two equal(in area) regions.Use only Eucledean tools.

$$\mathcal{T}{ake}\:{a}\:{point}\:\boldsymbol{{on}}\:{a}\:{given}\:{circle} \\ $$$${as}\:{a}\:{center}\:{and}\:{draw}\:{an}\:{arc} \\ $$$${which}\:{divide}\:{the}\:{given}\:{circle} \\ $$$${into}\:{two}\:{equal}\left(\mathrm{in}\:\mathrm{area}\right)\:{regions}.{Use}\:{only} \\ $$$${Eucledean}\:{tools}. \\ $$

Question Number 26711 Answers: 0 Comments: 1

ABC is a right tringle.prove it?

$$\mathrm{ABC}\:\mathrm{is}\:\mathrm{a}\:\mathrm{right}\:\mathrm{tringle}.\mathrm{prove}\:\mathrm{it}? \\ $$

Question Number 26652 Answers: 0 Comments: 2

Question Number 26644 Answers: 1 Comments: 0

Question Number 26389 Answers: 0 Comments: 1

Question Number 25963 Answers: 0 Comments: 0

A bus is traveling along a straight road at 100 km/hr and the bus conductor walks at 6 km/hr on the floor of the bus and in the same direction as the bus. Find the speed of the conductor relative to the road and relative to the bus.

Question Number 25930 Answers: 2 Comments: 0

A line passes through A(−3, 0) and B(0, −4). A variable line perpendicular to AB is drawn to cut x and y-axes at M and N. Find the locus of the point of intersection of the lines AN and BM.

$$\mathrm{A}\:\mathrm{line}\:\mathrm{passes}\:\mathrm{through}\:{A}\left(−\mathrm{3},\:\mathrm{0}\right)\:\mathrm{and} \\ $$$${B}\left(\mathrm{0},\:−\mathrm{4}\right).\:\mathrm{A}\:\mathrm{variable}\:\mathrm{line}\:\mathrm{perpendicular} \\ $$$$\mathrm{to}\:{AB}\:\mathrm{is}\:\mathrm{drawn}\:\mathrm{to}\:\mathrm{cut}\:{x}\:\mathrm{and}\:{y}-\mathrm{axes}\:\mathrm{at} \\ $$$${M}\:\mathrm{and}\:{N}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{the}\:\mathrm{point}\:\mathrm{of} \\ $$$$\mathrm{intersection}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lines}\:{AN}\:\mathrm{and}\:{BM}. \\ $$

Question Number 25609 Answers: 0 Comments: 4

Question Number 25605 Answers: 1 Comments: 4

Question Number 25602 Answers: 1 Comments: 1

Question Number 25479 Answers: 1 Comments: 0

Question Number 25375 Answers: 1 Comments: 0

what is HCF of(1/(3 )) (2/3) (1/4) ?

$${what}\:{is}\:{HCF}\:\:{of}\frac{\mathrm{1}}{\mathrm{3}\:\:}\:\frac{\mathrm{2}}{\mathrm{3}}\:\frac{\mathrm{1}}{\mathrm{4}}\:? \\ $$

Question Number 25344 Answers: 1 Comments: 0

If A and B are two points on a circle of radius r, then prove that mAB^(−) ≤2r.

$$\mathrm{If}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{are}\:\mathrm{two}\:\mathrm{points}\:\mathrm{on}\:\mathrm{a} \\ $$$$\mathrm{circle}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{r},\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{m}\overline {\mathrm{AB}}\leqslant\mathrm{2r}. \\ $$

Question Number 25350 Answers: 0 Comments: 0

If A and B are two points in the plane of a circle having radius r and mAB>2r ,prove that at least one of A or B is outside the circle.

$$\mathrm{If}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{are}\:\mathrm{two}\:\mathrm{points}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{plane}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{having} \\ $$$$\mathrm{radius}\:\mathrm{r}\:\mathrm{and}\:\mathrm{mAB}>\mathrm{2r}\:,\mathrm{prove}\:\mathrm{that}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one} \\ $$$$\mathrm{of}\:\mathrm{A}\:\mathrm{or}\:\mathrm{B}\:\mathrm{is}\:\mathrm{outside}\:\mathrm{the}\:\mathrm{circle}. \\ $$

Question Number 25290 Answers: 2 Comments: 0

∫((x dx)/(√(a^4 +x^4 )))

$$\int\frac{{x}\:{dx}}{\sqrt{{a}^{\mathrm{4}} +{x}^{\mathrm{4}} }} \\ $$

Question Number 25139 Answers: 1 Comments: 0

What is the real and the imaginary part of the complex number z = (− 1)^(1000003)

$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{real}\:\mathrm{and}\:\mathrm{the}\:\mathrm{imaginary}\:\mathrm{part}\:\mathrm{of}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{number}\:\:\:\mathrm{z}\:=\:\left(−\:\mathrm{1}\right)^{\mathrm{1000003}} \\ $$

Question Number 24831 Answers: 1 Comments: 0

∫_1 ^2 ∫_1 ^2 ln(x+y)dx dy

$$ \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \int_{\mathrm{1}} ^{\mathrm{2}} {ln}\left({x}+{y}\right){dx}\:{dy} \\ $$

Question Number 24778 Answers: 0 Comments: 4

Show that the shortest distance between two opposite edges a,d of a tetrahedron is 6V/adsin 𝛉, where θ is the angle between the edges and V is the volume of the tetrahedron.

$${Show}\:{that}\:{the}\:{shortest}\:{distance} \\ $$$${between}\:{two}\:{opposite}\:{edges}\:\boldsymbol{{a}},\boldsymbol{{d}}\: \\ $$$${of}\:{a}\:{tetrahedron}\:{is}\:\mathrm{6}\boldsymbol{{V}}/\boldsymbol{{ad}}\mathrm{sin}\:\boldsymbol{\theta}, \\ $$$${where}\:\theta\:{is}\:{the}\:{angle}\:{between}\:{the} \\ $$$${edges}\:{and}\:{V}\:{is}\:{the}\:{volume}\:{of}\:{the} \\ $$$${tetrahedron}. \\ $$

Question Number 24684 Answers: 0 Comments: 0

Let ABCD be a square and M, N points on sides AB, BC respectably, such that ∠MDN = 45°. If R is the midpoint of MN show that RP = RQ where P, Q are the points of intersection of AC with the lines MD, ND.

$$\mathrm{Let}\:{ABCD}\:\mathrm{be}\:\mathrm{a}\:\mathrm{square}\:\mathrm{and}\:{M},\:{N}\:\mathrm{points} \\ $$$$\mathrm{on}\:\mathrm{sides}\:{AB},\:{BC}\:\mathrm{respectably},\:\mathrm{such}\:\mathrm{that} \\ $$$$\angle{MDN}\:=\:\mathrm{45}°.\:\mathrm{If}\:{R}\:\mathrm{is}\:\mathrm{the}\:\mathrm{midpoint}\:\mathrm{of} \\ $$$${MN}\:\mathrm{show}\:\mathrm{that}\:{RP}\:=\:{RQ}\:\mathrm{where}\:{P},\:{Q} \\ $$$$\mathrm{are}\:\mathrm{the}\:\mathrm{points}\:\mathrm{of}\:\mathrm{intersection}\:\mathrm{of}\:{AC}\:\mathrm{with} \\ $$$$\mathrm{the}\:\mathrm{lines}\:{MD},\:{ND}. \\ $$

Question Number 24604 Answers: 2 Comments: 0

x^2 −xsin x−cos x=0

$${x}^{\mathrm{2}} −{x}\mathrm{sin}\:{x}−\mathrm{cos}\:{x}=\mathrm{0} \\ $$

Question Number 24303 Answers: 1 Comments: 0

Assertion: Enthalpy of combustion is negative. Reason: Combustion reaction can be exothermic or endothermic.

$$\boldsymbol{\mathrm{Assertion}}:\:\mathrm{Enthalpy}\:\mathrm{of}\:\mathrm{combustion}\:\mathrm{is} \\ $$$$\mathrm{negative}. \\ $$$$\boldsymbol{\mathrm{Reason}}:\:\mathrm{Combustion}\:\mathrm{reaction}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{exothermic}\:\mathrm{or}\:\mathrm{endothermic}. \\ $$

Pg 100 Pg 101 Pg 102 Pg 103 Pg 104 Pg 105 Pg 106 Pg 107 Pg 108 Pg 109

Contact: info@tinkutara.com