Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 17359 by ajfour last updated on 04/Jul/17

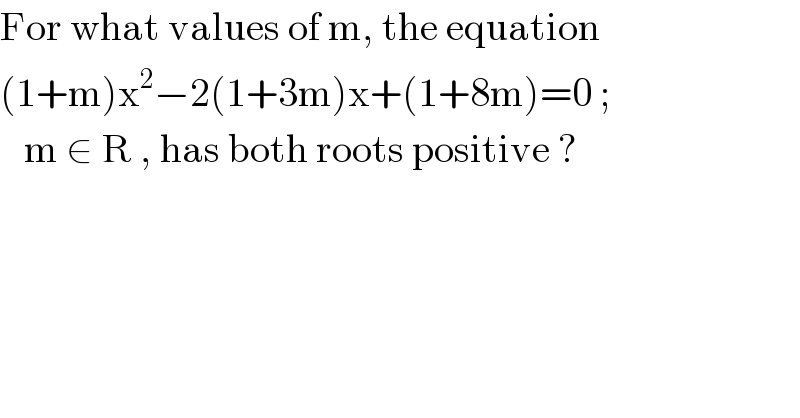
For what values of m, the equation (1+m)x^2 −2(1+3m)x+(1+8m)=0 ; m ∈ R , has both roots positive ?

$$\mathrm{For}\:\mathrm{what}\:\mathrm{values}\:\mathrm{of}\:\mathrm{m},\:\mathrm{the}\:\mathrm{equation} \\ $$$$\left(\mathrm{1}+\mathrm{m}\right)\mathrm{x}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}+\mathrm{3m}\right)\mathrm{x}+\left(\mathrm{1}+\mathrm{8m}\right)=\mathrm{0}\:; \\ $$$$\:\:\:\mathrm{m}\:\in\:\mathrm{R}\:,\:\mathrm{has}\:\mathrm{both}\:\mathrm{roots}\:\mathrm{positive}\:? \\ $$

Commented by ajfour last updated on 04/Jul/17

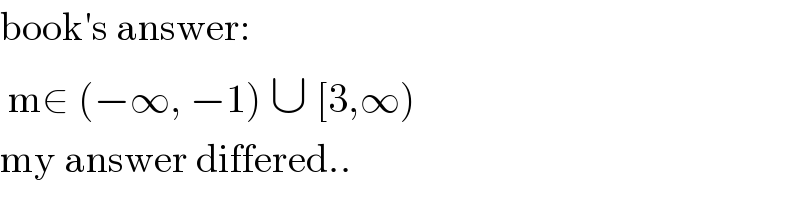
book′s answer: m∈ (−∞, −1) ∪ [3,∞) my answer differed..

$$\mathrm{book}'\mathrm{s}\:\mathrm{answer}: \\ $$$$\:\mathrm{m}\in\:\left(−\infty,\:−\mathrm{1}\right)\:\cup\:\left[\mathrm{3},\infty\right) \\ $$$$\mathrm{my}\:\mathrm{answer}\:\mathrm{differed}.. \\ $$

Commented by ajfour last updated on 04/Jul/17

thanks Sir. very precise.

$$\mathrm{thanks}\:\mathrm{Sir}.\:\mathrm{very}\:\mathrm{precise}. \\ $$

Commented by prakash jain last updated on 04/Jul/17

roots are ((−b)/(2a))±((√(b^2 −4ac))/(2a)) −(b/(2a)) lies in between roots condition for +ve roots>0 −(b/(2a))≥0,αβ>0,D≥0 (((1+3m))/((1+m)))≥0⇒m∈(−∞,−1)∪[−(1/3),∞) (((1+8m))/((1+m)))>0⇒m∈(−∞,−1)∪(−(1/8),∞) D=4{(1+3m)^2 −(1+m)(1+8m)}≥0 ⇒m(m−3)≥0⇒m∈(−∞,0]∪[3,∞) answer m∈(−∞,−1)∪(−(1/8),0]∪[3,∞)

$$\mathrm{roots}\:\mathrm{are}\:\frac{−\mathrm{b}}{\mathrm{2a}}\pm\frac{\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$$−\frac{{b}}{\mathrm{2}{a}}\:\mathrm{lies}\:\mathrm{in}\:\mathrm{between}\:\mathrm{roots} \\ $$$$\mathrm{condition}\:\mathrm{for}\:+\mathrm{ve}\:\mathrm{roots}>\mathrm{0} \\ $$$$−\frac{\mathrm{b}}{\mathrm{2a}}\geqslant\mathrm{0},\alpha\beta>\mathrm{0},{D}\geqslant\mathrm{0} \\ $$$$\frac{\left(\mathrm{1}+\mathrm{3}{m}\right)}{\left(\mathrm{1}+{m}\right)}\geqslant\mathrm{0}\Rightarrow{m}\in\left(−\infty,−\mathrm{1}\right)\cup\left[−\frac{\mathrm{1}}{\mathrm{3}},\infty\right) \\ $$$$\frac{\left(\mathrm{1}+\mathrm{8}{m}\right)}{\left(\mathrm{1}+{m}\right)}>\mathrm{0}\Rightarrow{m}\in\left(−\infty,−\mathrm{1}\right)\cup\left(−\frac{\mathrm{1}}{\mathrm{8}},\infty\right) \\ $$$${D}=\mathrm{4}\left\{\left(\mathrm{1}+\mathrm{3}{m}\right)^{\mathrm{2}} −\left(\mathrm{1}+{m}\right)\left(\mathrm{1}+\mathrm{8}{m}\right)\right\}\geqslant\mathrm{0} \\ $$$$\Rightarrow{m}\left({m}−\mathrm{3}\right)\geqslant\mathrm{0}\Rightarrow{m}\in\left(−\infty,\mathrm{0}\right]\cup\left[\mathrm{3},\infty\right) \\ $$$${answer} \\ $$$${m}\in\left(−\infty,−\mathrm{1}\right)\cup\left(−\frac{\mathrm{1}}{\mathrm{8}},\mathrm{0}\right]\cup\left[\mathrm{3},\infty\right) \\ $$

Commented by Tinkutara last updated on 05/Jul/17

ajfour Sir, which book is that? Can you please tell its description so that I can prepare well from it?

$$\mathrm{ajfour}\:\mathrm{Sir},\:\mathrm{which}\:\mathrm{book}\:\mathrm{is}\:\mathrm{that}?\:\mathrm{Can}\:\mathrm{you} \\ $$$$\mathrm{please}\:\mathrm{tell}\:\mathrm{its}\:\mathrm{description}\:\mathrm{so}\:\mathrm{that}\:\mathrm{I}\:\mathrm{can} \\ $$$$\mathrm{prepare}\:\mathrm{well}\:\mathrm{from}\:\mathrm{it}? \\ $$

Commented by ajfour last updated on 05/Jul/17

S.K. Goyal′s Algebra, Arihant Prakashan.

$$\mathrm{S}.\mathrm{K}.\:\mathrm{Goyal}'\mathrm{s}\:\mathrm{Algebra},\:\mathrm{Arihant} \\ $$$$\mathrm{Prakashan}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com