
Question Number 60849 by Kunal12588 last updated on 26/May/19
![For all θ in [0, π/2] show that cos(sinθ)≥sin(cosθ).](Q60849.png)
$${For}\:{all}\:\theta\:{in}\:\left[\mathrm{0},\:\pi/\mathrm{2}\right]\:{show}\:{that}\:{cos}\left({sin}\theta\right)\geqslant{sin}\left({cos}\theta\right). \\ $$
Commented by Prithwish sen last updated on 26/May/19
![when θ∈[0,(π/2) ] sinθ and cosθ lies between 0 to 1 ∴ For α∈[0,1] Cosα>Sinα for ∀ α ∈[0,1] i.e Cos(Sinθ)>Sin(Cosθ)](Q60857.png)
$$\mathrm{when}\:\theta\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\:\right] \\ $$$$\mathrm{sin}\theta\:\mathrm{and}\:\mathrm{cos}\theta\:\mathrm{lies}\:\mathrm{between}\:\mathrm{0}\:\mathrm{to}\:\mathrm{1} \\ $$$$\therefore\:\mathrm{For}\:\alpha\in\left[\mathrm{0},\mathrm{1}\right] \\ $$$$\mathrm{Cos}\alpha>\mathrm{Sin}\alpha\:\mathrm{for}\:\forall\:\alpha\:\in\left[\mathrm{0},\mathrm{1}\right] \\ $$$$\mathrm{i}.\mathrm{e}\:\mathrm{Cos}\left(\mathrm{Sin}\theta\right)>\mathrm{Sin}\left(\mathrm{Cos}\theta\right) \\ $$
Commented by Kunal12588 last updated on 26/May/19

$${thanks}\:{sir} \\ $$
Commented by Kunal12588 last updated on 26/May/19
![but i don′t get it sir how cos α > sin α ∀ α∈ [0,1]](Q60871.png)
$${but}\:{i}\:{don}'{t}\:{get}\:{it}\:{sir}\:{how}\: \\ $$$${cos}\:\alpha\:>\:{sin}\:\alpha\:\:\forall\:\alpha\in\:\left[\mathrm{0},\mathrm{1}\right]\: \\ $$
Commented by Prithwish sen last updated on 26/May/19
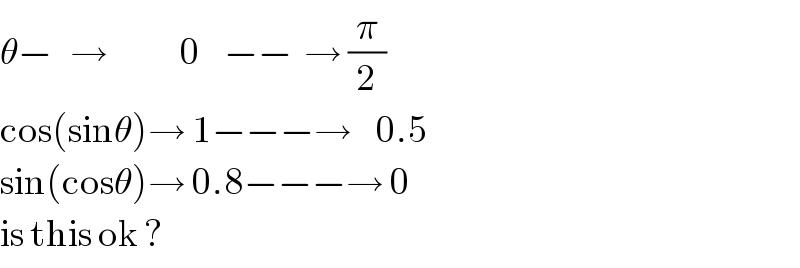
$$\theta−\:\:\:\rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:−−\:\:\rightarrow\:\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{cos}\left(\mathrm{sin}\theta\right)\rightarrow\:\mathrm{1}−−−\rightarrow\:\:\:\:\mathrm{0}.\mathrm{5} \\ $$$$\mathrm{sin}\left(\mathrm{cos}\theta\right)\rightarrow\:\mathrm{0}.\mathrm{8}−−−\rightarrow\:\mathrm{0} \\ $$$$\mathrm{is}\:\mathrm{this}\:\mathrm{ok}\:? \\ $$
Commented by Kunal12588 last updated on 26/May/19
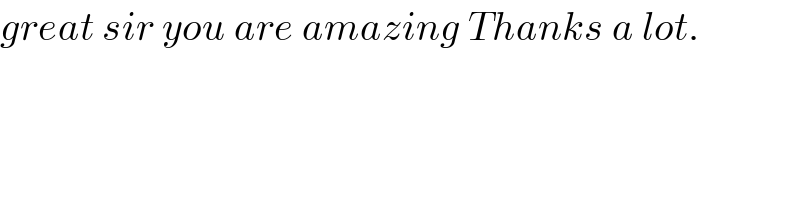
$${great}\:{sir}\:{you}\:{are}\:{amazing}\:{Thanks}\:{a}\:{lot}. \\ $$
Answered by tanmay last updated on 26/May/19
![when θ∈[0,(π/2)] sinθ∈[0,1] so cos(sinθ)∈[cos1,1] when θ∈[0,(π/2)] cosθ∈[0,1] so sin(cosθ)∈[0,sin1] cos1>0 1>sin1 so cos(sinθ)>sin(cosθ) attaching graph...](Q60851.png)
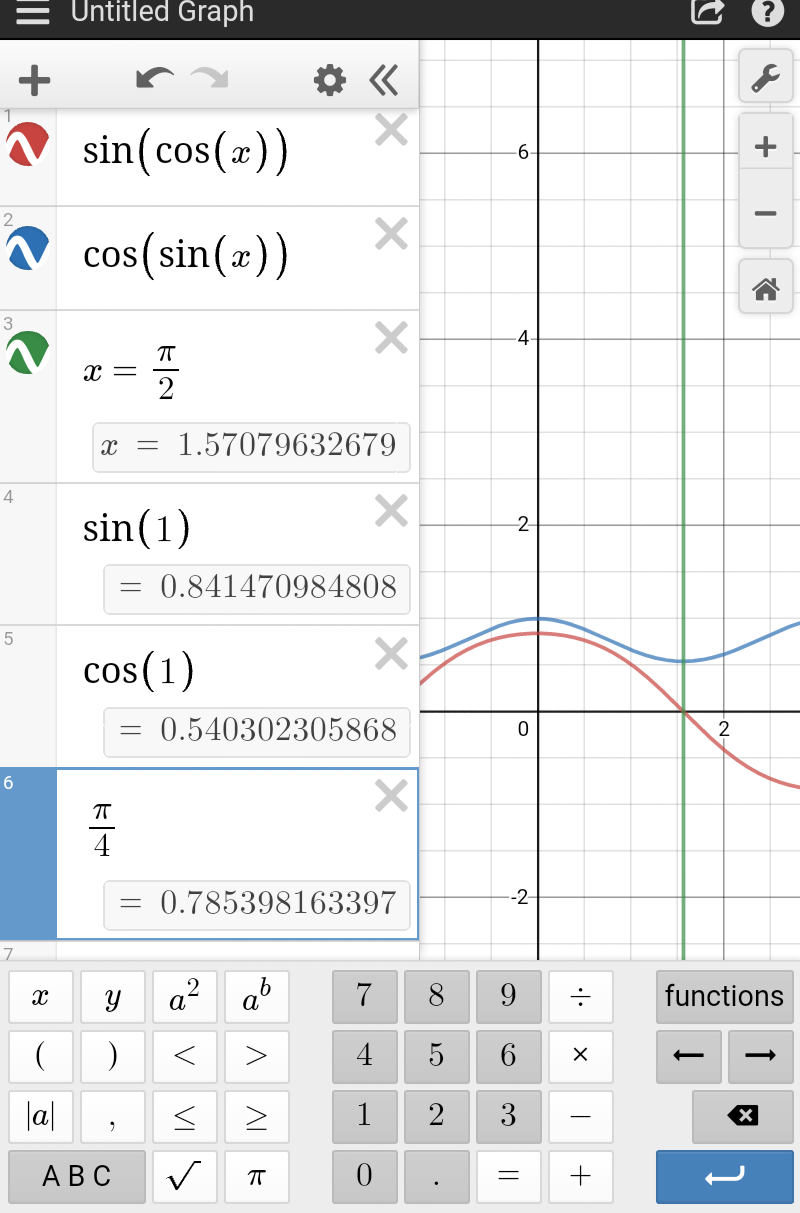
$${when}\:\theta\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\:{sin}\theta\in\left[\mathrm{0},\mathrm{1}\right]\:{so}\:{cos}\left({sin}\theta\right)\in\left[{cos}\mathrm{1},\mathrm{1}\right] \\ $$$${when}\:\theta\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\:{cos}\theta\in\left[\mathrm{0},\mathrm{1}\right]\:{so}\:{sin}\left({cos}\theta\right)\in\left[\mathrm{0},{sin}\mathrm{1}\right] \\ $$$${cos}\mathrm{1}>\mathrm{0} \\ $$$$\mathrm{1}>{sin}\mathrm{1} \\ $$$${so}\:{cos}\left({sin}\theta\right)>{sin}\left({cos}\theta\right) \\ $$$${attaching}\:{graph}... \\ $$
Commented by tanmay last updated on 26/May/19
Commented by Kunal12588 last updated on 26/May/19

$${thank}\:{you}\:{sir} \\ $$
Commented by Kunal12588 last updated on 26/May/19
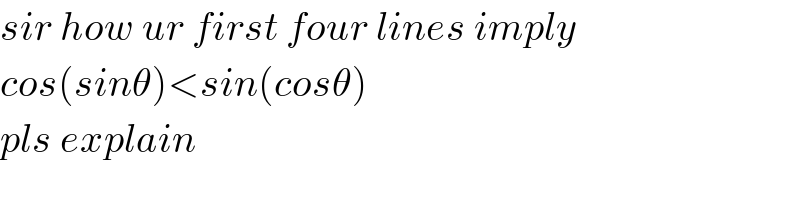
$${sir}\:{how}\:{ur}\:{first}\:{four}\:{lines}\:{imply} \\ $$$${cos}\left({sin}\theta\right)<{sin}\left({cos}\theta\right) \\ $$$${pls}\:{explain} \\ $$
Commented by tanmay last updated on 26/May/19

$${pls}\:{refer}\:{the}\:{graph}\:...{all}\:{problems}\:{can}\:{not}\:{besolved}\:{simply} \\ $$$${by}\:{mathematics}...{it}\:{is}\:{better}\:{to}\:{see}\:{the}\:{graphs}.. \\ $$$$ \\ $$
Commented by Kunal12588 last updated on 26/May/19
$${thanks}\:{sir}\:{graphs}\:{clarifies}\:{the}\:{thing}. \\ $$
