Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 86242 by niroj last updated on 27/Mar/20

Find y=CF+PI in following differential equation: (d^2 y/dx^2 )+3(dy/dx)+2y= e^(2x) sinx .

$$\:\boldsymbol{\mathrm{Find}}\:\:\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{C}}\mathrm{F}+\boldsymbol{\mathrm{P}}\mathrm{I}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{following}}\:\boldsymbol{\mathrm{differential}}\:\boldsymbol{\mathrm{equation}}: \\ $$$$\:\:\:\frac{\boldsymbol{\mathrm{d}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{2}} }+\mathrm{3}\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}+\mathrm{2}\boldsymbol{\mathrm{y}}=\:\boldsymbol{\mathrm{e}}^{\mathrm{2}\boldsymbol{\mathrm{x}}} \:\boldsymbol{\mathrm{sinx}}\:. \\ $$$$\: \\ $$$$ \\ $$

Answered by TANMAY PANACEA. last updated on 27/Mar/20

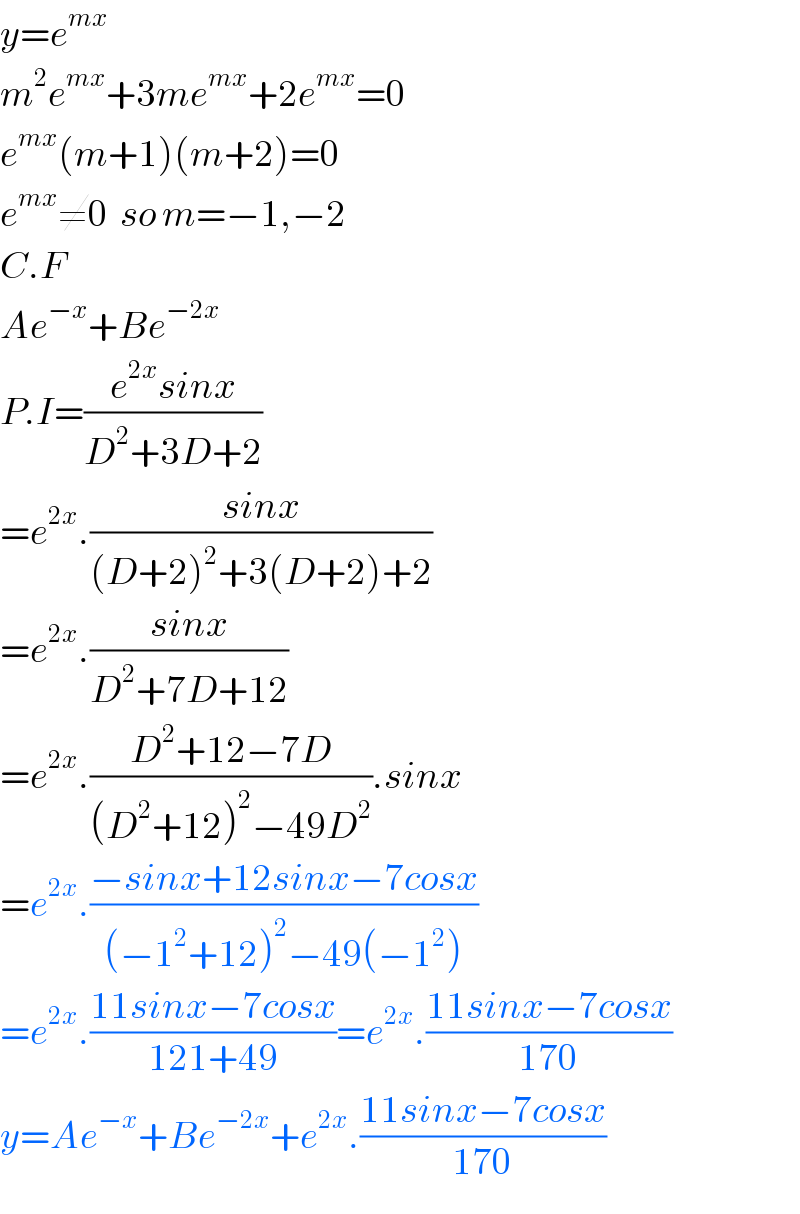
y=e^(mx) m^2 e^(mx) +3me^(mx) +2e^(mx) =0 e^(mx) (m+1)(m+2)=0 e^(mx) ≠0 so m=−1,−2 C.F Ae^(−x) +Be^(−2x) P.I=((e^(2x) sinx)/(D^2 +3D+2)) =e^(2x) .((sinx)/((D+2)^2 +3(D+2)+2)) =e^(2x) .((sinx)/(D^2 +7D+12)) =e^(2x) .((D^2 +12−7D)/((D^2 +12)^2 −49D^2 )).sinx =e^(2x) .((−sinx+12sinx−7cosx)/((−1^2 +12)^2 −49(−1^2 ))) =e^(2x) .((11sinx−7cosx)/(121+49))=e^(2x) .((11sinx−7cosx)/(170)) y=Ae^(−x) +Be^(−2x) +e^(2x) .((11sinx−7cosx)/(170))

$${y}={e}^{{mx}} \: \\ $$$${m}^{\mathrm{2}} {e}^{{mx}} +\mathrm{3}{me}^{{mx}} +\mathrm{2}{e}^{{mx}} =\mathrm{0} \\ $$$${e}^{{mx}} \left({m}+\mathrm{1}\right)\left({m}+\mathrm{2}\right)=\mathrm{0} \\ $$$${e}^{{mx}} \neq\mathrm{0}\:\:{so}\:{m}=−\mathrm{1},−\mathrm{2} \\ $$$${C}.{F} \\ $$$${Ae}^{−{x}} +{Be}^{−\mathrm{2}{x}} \\ $$$${P}.{I}=\frac{{e}^{\mathrm{2}{x}} {sinx}}{{D}^{\mathrm{2}} +\mathrm{3}{D}+\mathrm{2}} \\ $$$$={e}^{\mathrm{2}{x}} .\frac{{sinx}}{\left({D}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{3}\left({D}+\mathrm{2}\right)+\mathrm{2}} \\ $$$$={e}^{\mathrm{2}{x}} .\frac{{sinx}}{{D}^{\mathrm{2}} +\mathrm{7}{D}+\mathrm{12}} \\ $$$$={e}^{\mathrm{2}{x}} .\frac{{D}^{\mathrm{2}} +\mathrm{12}−\mathrm{7}{D}}{\left({D}^{\mathrm{2}} +\mathrm{12}\right)^{\mathrm{2}} −\mathrm{49}{D}^{\mathrm{2}} }.{sinx} \\ $$$$={e}^{\mathrm{2}{x}} .\frac{−{sinx}+\mathrm{12}{sinx}−\mathrm{7}{cosx}}{\left(−\mathrm{1}^{\mathrm{2}} +\mathrm{12}\right)^{\mathrm{2}} −\mathrm{49}\left(−\mathrm{1}^{\mathrm{2}} \right)} \\ $$$$={e}^{\mathrm{2}{x}} .\frac{\mathrm{11}{sinx}−\mathrm{7}{cosx}}{\mathrm{121}+\mathrm{49}}={e}^{\mathrm{2}{x}} .\frac{\mathrm{11}{sinx}−\mathrm{7}{cosx}}{\mathrm{170}} \\ $$$${y}={Ae}^{−{x}} +{Be}^{−\mathrm{2}{x}} +{e}^{\mathrm{2}{x}} .\frac{\mathrm{11}{sinx}−\mathrm{7}{cosx}}{\mathrm{170}} \\ $$

Commented by niroj last updated on 27/Mar/20

great job sir.

$$\mathrm{great}\:\mathrm{job}\:\mathrm{sir}. \\ $$

Commented by TANMAY PANACEA. last updated on 27/Mar/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com